陕西省延安市富县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 若m是一元二次方程 的根,则 的值为( )A、1 B、-1 C、2 D、-22. 古钱币是我国悠久的历史文化遗产,以下是在《中国古代钱币》特种邮票中选取的部分图形,其中既是轴对称图形又是中心对称图形的是( )
 A、
A、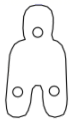 B、
B、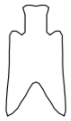 C、
C、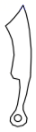 D、
D、 3. 关于x的方程 能直接开平方求解的条件是( )A、 , B、 , C、a为任意数且 D、a为任意数且4. 一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是必然事件的是( )A、3个球都是黑球 B、3个球都是白球 C、3个球中有黑球 D、3个球中有白球5. 在平面直角坐标系中,点 与点 关于( )A、x轴对称 B、y轴对称 C、原点对称 D、直线 对称6. 一个质地均匀的小正方体,六个面上分别标有数字1、2、3、4、5、6,掷小正方体后,观察朝上一面的数字出现偶数的概率是( )A、 B、 C、 D、7. 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
3. 关于x的方程 能直接开平方求解的条件是( )A、 , B、 , C、a为任意数且 D、a为任意数且4. 一个不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是必然事件的是( )A、3个球都是黑球 B、3个球都是白球 C、3个球中有黑球 D、3个球中有白球5. 在平面直角坐标系中,点 与点 关于( )A、x轴对称 B、y轴对称 C、原点对称 D、直线 对称6. 一个质地均匀的小正方体,六个面上分别标有数字1、2、3、4、5、6,掷小正方体后,观察朝上一面的数字出现偶数的概率是( )A、 B、 C、 D、7. 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )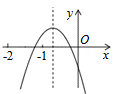 A、a<0 B、b<0 C、c<0 D、a<b8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( )
A、a<0 B、b<0 C、c<0 D、a<b8. 如图,已知E是 的外心,P,Q分别是 , 的中点,连接 , ,分别交 于点F,D.若 , , ,则 的面积为( ) A、72 B、96 C、120 D、1449. 如图, 是 的直径, ,则 的度数为( )
A、72 B、96 C、120 D、1449. 如图, 是 的直径, ,则 的度数为( ) A、 B、 C、 D、10. 将抛物线 向左平移1个单位长度,得到抛物线 ,抛物线 与抛物线 关于x轴对称,则抛物线 的解析式为( )A、 B、 C、 D、
A、 B、 C、 D、10. 将抛物线 向左平移1个单位长度,得到抛物线 ,抛物线 与抛物线 关于x轴对称,则抛物线 的解析式为( )A、 B、 C、 D、二、填空题
-
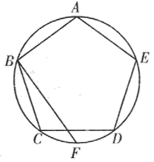
11. 关于x的方程 是一元二次方程,则m的值为.12. 如图,正五边形 内接于 ,F是 的中点,则 的度数为.
 13. 某幢建筑物,从5米高的窗口A用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图所示),如果抛物线的最高点M离墙1米,离地面 米,则水流下落点B离墙距离OB是m.
13. 某幢建筑物,从5米高的窗口A用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图所示),如果抛物线的最高点M离墙1米,离地面 米,则水流下落点B离墙距离OB是m. 14. 如图, 是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在 边上,若 , ,则 的长为.
14. 如图, 是 的边 上的中线,将线段 绕点D顺时针旋转 后,点A的对应点E恰好落在 边上,若 , ,则 的长为.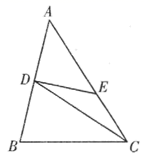
三、解答题
-
15. 解方程: .16. 如图,△ABC由△EDC绕C点旋转得到,B、C、E三点在同一条直线上,∠ACD=∠B,求证:△ABC是等腰三角形.
 17. 如图,每个小方格的边长为1个单位, 的顶点都在格点上,且 , ,先在图中建立适当的直角坐标系,再画出 关于坐标原点对称的图形.
17. 如图,每个小方格的边长为1个单位, 的顶点都在格点上,且 , ,先在图中建立适当的直角坐标系,再画出 关于坐标原点对称的图形. 18. 4件同型号的产品中,有1件不合格品和3件合格品.在这4件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,由此可以推算出 的值大约是多少?19. 某旅游景区今年9月份游客人数比8月份增加了 ,10月份游客人数比9月份增加了 ,求该旅游景区9,10两个月游客人数的平均增长率.20. 某灯具厂生产一批台灯罩,如图的阴影部分为灯罩的侧面展开图.已知半径 , , .(计算结果保留 )
18. 4件同型号的产品中,有1件不合格品和3件合格品.在这4件产品中加入 件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,由此可以推算出 的值大约是多少?19. 某旅游景区今年9月份游客人数比8月份增加了 ,10月份游客人数比9月份增加了 ,求该旅游景区9,10两个月游客人数的平均增长率.20. 某灯具厂生产一批台灯罩,如图的阴影部分为灯罩的侧面展开图.已知半径 , , .(计算结果保留 ) (1)、若要在灯罩的上下边缘镶上花边(花边的宽度忽略不计),至少需要多长的花边?(2)、求灯罩的侧面积(接缝处忽略不计).21. 已知抛物线 ( 为常数)的对称轴是y轴,并且与x轴有两个交点.(1)、求k的值;(2)、若点P在抛物线 上,且点P到y轴的距离是2,求点P的坐标.22. 手机微信中的抢红包游戏有一种玩法为“拼手气红包”:用户设定好总金额以及红包个数之后,可以生成不等金额的红包.现有四个人组成的微信群中,其中一人发了三个“拼手气红包”,其他三人(甲、乙、丙)随机抢红包.(1)、若甲的速度最快,求甲抢到最多金额的红包的概率;(2)、若三个人同时点开红包,记金额最多、居中、最少的红包分别为A、B、C,请用画树状图或列表的方法求甲抢到红包A的概率.23. 如图,已知 的直径 ,弦 , 的平分线交 于点D,过点D作 ,交 的延长线于点E.
(1)、若要在灯罩的上下边缘镶上花边(花边的宽度忽略不计),至少需要多长的花边?(2)、求灯罩的侧面积(接缝处忽略不计).21. 已知抛物线 ( 为常数)的对称轴是y轴,并且与x轴有两个交点.(1)、求k的值;(2)、若点P在抛物线 上,且点P到y轴的距离是2,求点P的坐标.22. 手机微信中的抢红包游戏有一种玩法为“拼手气红包”:用户设定好总金额以及红包个数之后,可以生成不等金额的红包.现有四个人组成的微信群中,其中一人发了三个“拼手气红包”,其他三人(甲、乙、丙)随机抢红包.(1)、若甲的速度最快,求甲抢到最多金额的红包的概率;(2)、若三个人同时点开红包,记金额最多、居中、最少的红包分别为A、B、C,请用画树状图或列表的方法求甲抢到红包A的概率.23. 如图,已知 的直径 ,弦 , 的平分线交 于点D,过点D作 ,交 的延长线于点E. (1)、求证: 是 的切线;(2)、求 的长.24. 如图,抛物线 经过点 ,与 轴的另一个交点为 ,与 轴交于点 .
(1)、求证: 是 的切线;(2)、求 的长.24. 如图,抛物线 经过点 ,与 轴的另一个交点为 ,与 轴交于点 .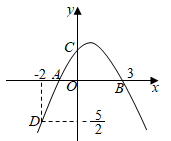 (1)、求该抛物线的表达式;(2)、点 在该抛物线上,点 在 轴上,要使以点 为顶点的四边形是平行四边形,求所有满足条件的点 的坐标.25.
(1)、求该抛物线的表达式;(2)、点 在该抛物线上,点 在 轴上,要使以点 为顶点的四边形是平行四边形,求所有满足条件的点 的坐标.25. (1)、问题提出
(1)、问题提出如图①, 内接于半径为4的 , 是 的中位线,则 的最大值是;
(2)、问题探究如图②,在等腰 中, , , 边上的中线 ,求等腰 外接圆的半径;
(3)、问题解决如图③,工人师傅现要在一张足够大的板材上剪裁出一个形状为 的部件,已知 的部件要满足 , 边上的中线 ,且边 与边 之和要最大,是否能剪裁出满足要求的三角形部件?若能,请求出 的最大值;若不能,请说明理由.