陕西省渭南市富平县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 计算 的结果是 ( )A、 B、 C、 D、2. 下列几何体的左视图和俯视图相同的是( )A、
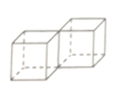 B、
B、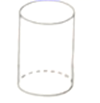 C、
C、 D、
D、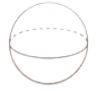 3. 抛物线y=(x-4) 2-3的顶点坐标是( )A、(-4,3) B、(-4,-3) C、(4,3) D、(4,-3)4. 在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )A、不能够确定谁的影子长 B、小刚的影子比小红的影子短 C、小刚跟小红的影子一样长 D、小刚的影子比小红的影子长5. 在平面直角坐标系中的位置如图所示,已知点A的坐标为 , 与 关于点О成位似图形,且在点О的同一侧, 与 的位似比为1:2,则点A的对应点 的坐标是( )
3. 抛物线y=(x-4) 2-3的顶点坐标是( )A、(-4,3) B、(-4,-3) C、(4,3) D、(4,-3)4. 在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )A、不能够确定谁的影子长 B、小刚的影子比小红的影子短 C、小刚跟小红的影子一样长 D、小刚的影子比小红的影子长5. 在平面直角坐标系中的位置如图所示,已知点A的坐标为 , 与 关于点О成位似图形,且在点О的同一侧, 与 的位似比为1:2,则点A的对应点 的坐标是( )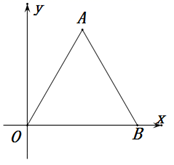 A、 B、 C、 D、6. 反比例函数 ( 为常数)的图象位于第一、三象限,则m的取值范围是( )A、 B、 C、 D、7. 如图,在 中, 平分 , 交 于点E, 交 于点F,且 交 于点O,若 ,则 的值为( )
A、 B、 C、 D、6. 反比例函数 ( 为常数)的图象位于第一、三象限,则m的取值范围是( )A、 B、 C、 D、7. 如图,在 中, 平分 , 交 于点E, 交 于点F,且 交 于点O,若 ,则 的值为( ) A、 B、 C、 D、8. 由于国内疫情得到缓和,餐饮业逐渐恢复,某地一家餐厅重新开张,开业第一天收入约为2000元,之后两天的收入按相同的增长率增长,第3天的收入约为2420元,若设每天的增长率为x,则列方程为( )A、 B、 C、 D、9. 已知关于x的方程 有两个相等的实数根,且反比例函数 的图象在每个象限内y随x的增大而增大,那么m的值为( )A、-1 B、3或-1 C、-2 D、310. 如图,二次函数 (a、b、c是常数,且 )的图象与x轴的一个交点为 ,对称轴为直线 ,下列结论:① ;② ;③ ;④ .其中正确结论的个数为( )
A、 B、 C、 D、8. 由于国内疫情得到缓和,餐饮业逐渐恢复,某地一家餐厅重新开张,开业第一天收入约为2000元,之后两天的收入按相同的增长率增长,第3天的收入约为2420元,若设每天的增长率为x,则列方程为( )A、 B、 C、 D、9. 已知关于x的方程 有两个相等的实数根,且反比例函数 的图象在每个象限内y随x的增大而增大,那么m的值为( )A、-1 B、3或-1 C、-2 D、310. 如图,二次函数 (a、b、c是常数,且 )的图象与x轴的一个交点为 ,对称轴为直线 ,下列结论:① ;② ;③ ;④ .其中正确结论的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 已知 是关于x的一元二次方程 的一个根,则m的值为.12. 袋中装有6个黑球和若干个白球,每个球除颜色外都相同.现进行摸球试验,每次随机摸出一个球记下颜色后放回,经过大量的试验,发现摸到黑球的频率稳定在0.75附近,则袋中白球约有个。13. 分别以矩形 的边OA,OC所在的直线为x轴,y轴建立平面直角坐标系,点B的坐标是(4,2),将矩形 折叠使点B落在G(3,0)上,折痕为 ,若反比例函数 的图象恰好经过点E,则k的值为.
 14. 如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .
14. 如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .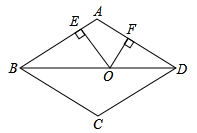
三、解答题
-
15. 用配方法解方程: .16. 图中几何体是将大长方体内部挖去一个小长方休后剩余的部分,请画出该几何体的三视图.
 17. 如图,在三角形ABC中,∠ACB=90°,CD⊥AB交AB于D,AD=4,BD=9,求tanA.
17. 如图,在三角形ABC中,∠ACB=90°,CD⊥AB交AB于D,AD=4,BD=9,求tanA.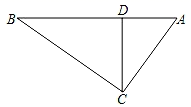 18. 在平面直角坐标系中,抛物线的表达式为 .将抛物线向左平移2个单位后,恰经过点 ,求b的值.19. 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度y(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升 时,满足 ,下降时,y与x成反比例关系.
18. 在平面直角坐标系中,抛物线的表达式为 .将抛物线向左平移2个单位后,恰经过点 ,求b的值.19. 某药品研究所研发一种抗菌新药,测得成人服用该药后血液中的药物浓度y(微克/毫升)与服药后时间x(小时)之间的函数关系如图所示,当血液中药物浓度上升 时,满足 ,下降时,y与x成反比例关系.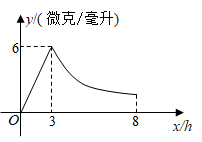 (1)、求a的值,并求当 时,y与x的函数表达式;(2)、血液中药物浓度不低于3微克/毫升的持续时间是多少小时?20. 小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为38米,塔的顶端为点A,且 ,在点E处竖直放一根标杆,其顶端为D, ,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得 米.已知标杆 米,求该塔的高度AB.
(1)、求a的值,并求当 时,y与x的函数表达式;(2)、血液中药物浓度不低于3微克/毫升的持续时间是多少小时?20. 小雁塔位于西安市南郊的荐福寺内,又称“荐福寺塔”,建于唐景龙年间,与大雁塔同为唐长安城保留至今的重要标志.数学活动小组的同学对该塔进行了测量,测量方法如下:如图所示,间接测得该塔底部点B到地面上一点E的距离为38米,塔的顶端为点A,且 ,在点E处竖直放一根标杆,其顶端为D, ,在BE的延长线上找一点C,使C,D,A三点在同一直线上,测得 米.已知标杆 米,求该塔的高度AB.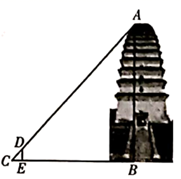 21. 如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合), ,且 .求证:四边形ABCD是正方形.
21. 如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合), ,且 .求证:四边形ABCD是正方形. 22. 甲、乙,丙、丁4人聚会,每人带了一件礼物,4件礼物从外盒包装看完全相同,将4件礼物放在一起.(1)、甲从中随机抽取一件,求甲抽到的是自己带来的礼物的概率;(2)、甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,用列表法或画树状图法求甲、乙2人抽到的都不是自己带来的礼物的概率.23. 如图1,矩形ABCD中,已知 , ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将 沿直线AE翻折,点B的对应点为点 ,延长 交CD于点M.
22. 甲、乙,丙、丁4人聚会,每人带了一件礼物,4件礼物从外盒包装看完全相同,将4件礼物放在一起.(1)、甲从中随机抽取一件,求甲抽到的是自己带来的礼物的概率;(2)、甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,用列表法或画树状图法求甲、乙2人抽到的都不是自己带来的礼物的概率.23. 如图1,矩形ABCD中,已知 , ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将 沿直线AE翻折,点B的对应点为点 ,延长 交CD于点M.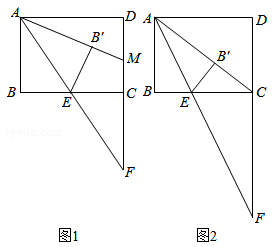 (1)、求证: ;(2)、如图2,若点 恰好落在对角线 上,求 的值.
(1)、求证: ;(2)、如图2,若点 恰好落在对角线 上,求 的值.

