宁夏回族自治区石嘴山市平罗县2021届九年级上学期数学期末考试试卷
试卷更新日期:2021-03-30 类型:期末考试
一、单选题
-
1. 下列是一元二次方程的是( )A、 B、 C、 D、2. 下列事件为必然事件的是( )A、掷一枚均匀的骰子,朝上的面点数为奇数 B、某射击运动员射靶一次,正中靶心 C、打开电视,正在播足球比赛 D、口袋中装有1个红球和2个白球,从中摸出2个球,其中必有白球3. 将抛物线y=2x2向下平移3个单位长度所得到的抛物线是( )A、y=2x2+3 B、y=2x2﹣3 C、y=2(x﹣3)2 D、y=2(x+3)24. 下列图形中,既是轴对称又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 小明制作了5张卡片,上面分别写了一个条件:① ;② ;③ ;④ ,⑤ .从中随机抽取一张卡片,能判定 是菱形的概率为( )A、 B、 C、 D、6. 关于x的方程x2﹣kx﹣2=0的根的情况是( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定7. 已知二次函数y=a(x−1)2−c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
5. 小明制作了5张卡片,上面分别写了一个条件:① ;② ;③ ;④ ,⑤ .从中随机抽取一张卡片,能判定 是菱形的概率为( )A、 B、 C、 D、6. 关于x的方程x2﹣kx﹣2=0的根的情况是( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法确定7. 已知二次函数y=a(x−1)2−c的图象如图所示,则一次函数y=ax+c的大致图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 如图,直径为10的 经过点 和点 , 是 轴右侧 优弧上一点, ,则点 的坐标为( )
8. 如图,直径为10的 经过点 和点 , 是 轴右侧 优弧上一点, ,则点 的坐标为( )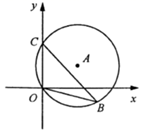 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若 是关于x的方程 的一个根,则a的值为.10. 若点 与点 关于原点 中心对称,则 .11. 在一个盒子中有红球,黑球,黄球共20个,每个球除颜色外都相同,从中任意摸出一球,得到红球的概率为 ,得到黑球的概率为 ,则这20个球中黄球有个.12. 如果抛物线 的开口向下,那么k的取值范围是 .13. 已知点 , , 在抛物 上,则 , , 的大系是.14. 如图,点A(﹣4,2)和B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,则不等式kx+b< 的解集是.
 15. 如图, 的顶点B、C、D在半圆O上,顶点E在直径 上,连接 ,若 ,则 的度数为度.
15. 如图, 的顶点B、C、D在半圆O上,顶点E在直径 上,连接 ,若 ,则 的度数为度.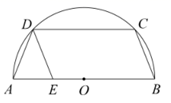 16. 如图,在正方形 中, ,点E在 边上, ,把 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为.
16. 如图,在正方形 中, ,点E在 边上, ,把 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为.
三、解答题
-
17. 解方程18. 用描点法画函数 的图象.
x
...
-3
-2
-1
0
1
2
3
...
y
...
19. 受益于新能源产业的高速发展,我市某汽车零部件生产企业的利润猪年提高,据统计, 年利润为 亿元, 年利润为 亿元,求该企业从 年到 年利润的年平均增长率20. 交大附中 各班举行了“垃圾分类,从我做起”的主题班会,九年级三班的同学在班会课上进行了一个有关垃圾分类知识竞答的活动,他们上网查阅了相关资料,收集到如下四个图标,并将其制成编号为 的四张卡片(除编号和内容外,其余完全相同) ,他们将这四张卡片背面朝上,洗匀放好. (1)、从中随机抽取一张,恰好抽到“可回收物”的概率是(2)、从中随机抽取一张(不放回),再从中随机抽一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“其他垃圾”和“有害垃圾”的概率(这四张卡片分别用它们的编号 表示)21. 如图,已知AB是⊙O的直径,C、D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)、从中随机抽取一张,恰好抽到“可回收物”的概率是(2)、从中随机抽取一张(不放回),再从中随机抽一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“其他垃圾”和“有害垃圾”的概率(这四张卡片分别用它们的编号 表示)21. 如图,已知AB是⊙O的直径,C、D是⊙O上的点,OC∥BD,交AD于点E,连结BC. (1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求扇形AOC的面积.22. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,1)、B(5,1)、C(4,4),按下列要求作图:
(1)、求证:AE=ED;(2)、若AB=10,∠CBD=36°,求扇形AOC的面积.22. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(1,1)、B(5,1)、C(4,4),按下列要求作图:
( 1 ) 将△ABC向左平移5个单位得到△A1B1C1 , 并写出点A1的坐标;
( 2 )将△ABC绕原点O逆时针旋转90°后得到△A2B2C2 , 并写出点B2的坐标;
23. 如图,已知 AB是⊙O的直径,点C在⊙O上,AD⊥DC于点 D,AC平分∠DAB. (1)、求证:直线CD是⊙O的切线;(2)、若 AB=4,∠DAB=60°,求AD的长.24. 我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓。某市某电器商场根据民众健康需要,代理销售某种空气净化器,其进价时 元/台。经过市场销售后发现:在一个月内,当售价是 元/台时,可售出 台,且售价每降低 元,就可多售出 台。若供货商规定这种空气净化器售价不能低于 元/台,代理销售商每月要完成不低于 台的销售任务。(1)、求出月销售量y(单位:台)与售价x(单位:元/台)之间的函数关系式,并求出自变量x的取值范围;(2)、当售价x定为多少时,商场每月销售这种空气净化器所获得的利润w(单位:元)最大?最大利润是多少?25. 在直角坐标系内的位置如图所示, ,反比例函数 在第一象限内的图象与 交于点 与 交于点 .
(1)、求证:直线CD是⊙O的切线;(2)、若 AB=4,∠DAB=60°,求AD的长.24. 我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓。某市某电器商场根据民众健康需要,代理销售某种空气净化器,其进价时 元/台。经过市场销售后发现:在一个月内,当售价是 元/台时,可售出 台,且售价每降低 元,就可多售出 台。若供货商规定这种空气净化器售价不能低于 元/台,代理销售商每月要完成不低于 台的销售任务。(1)、求出月销售量y(单位:台)与售价x(单位:元/台)之间的函数关系式,并求出自变量x的取值范围;(2)、当售价x定为多少时,商场每月销售这种空气净化器所获得的利润w(单位:元)最大?最大利润是多少?25. 在直角坐标系内的位置如图所示, ,反比例函数 在第一象限内的图象与 交于点 与 交于点 . (1)、求该反比例函数的解析式及图象为直线 的正比例函数解析式;(2)、求 的长.26. 如图,抛物线 经过 , 两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴 交x轴于点E,连接 .
(1)、求该反比例函数的解析式及图象为直线 的正比例函数解析式;(2)、求 的长.26. 如图,抛物线 经过 , 两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴 交x轴于点E,连接 . (1)、求经过 三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若 是以 为直角边的直角三角形,求点Q的坐标;(3)、若P为 的中点,过点P作 轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线 上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
(1)、求经过 三点的抛物线的函数表达式;(2)、点Q在该抛物线的对称轴上,若 是以 为直角边的直角三角形,求点Q的坐标;(3)、若P为 的中点,过点P作 轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线 上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.