江苏省南京市玄武区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-30 类型：期末考试

进入出卷网下载

一、单选题

1. 一元二次方程 $x^{2} - 4 = 0$ 的解是（）

A、 $x = - 2$ B、 $x = 2$ C、 $x = 4$ D、 $x_{1} = 2$ ， $x_{2} = - 2$

查看试题解析
2. 已知一组数据2，3，5，3，7，关于这组数据，下列说法不正确的是（）

A、平均数是4 B、众数是3 C、中位数是5 D、极差是5

查看试题解析
3. 如图，点A，B，C，D在 $⊙ O$ 上， $O A ⊥ B C$ ，若 $∠ B = 50 °$ ，则 $∠ D$ 的度数为（）

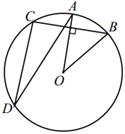A、20° B、25° C、30° D、40°

查看试题解析
4. 如图，直线 $l_{1} // l_{2} // l_{3}$ ，直线a、b与 $l_{1}$ 、 $l_{2}$ 、 $l_{3}$ 分别交于点A，B，C和点D，E，F，若 $A B ： B C = 1 ： 2$ ， $D F = 6$ ，则 $E F$ 的长为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 二次函数 $y = a x^{2} + b x + c$ （a、b、c是常数，且 $a \neq 0$ ）的图象如图所示，对称轴为直线 $x = - 1$ .下列结论：① $a b c < 0$ ；② $2 a - b = 0$ ；③ $a - b + c > 0$ ；④ $9 a - 3 b + c < 0$ .其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在 $△ A B C$ 中，D、E分别是 $A B$ 、 $B C$ 边上的点，连接 $D E$ 并延长，与 $A C$ 的延长线交于点F，且 $A D = 3 B D$ ， $E F = 2 D E$ ，若 $C F = 2$ ，则 $A F$ 的长为（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

7. 若 $\frac{a}{b} = \frac{3}{4}$ ，则 $\frac{b}{a + b} =$ .

查看试题解析
8. 若 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - 2 x - 1 = 0$ 的两个实数根，则 $x_{1}^{2} + x_{2}^{2} + 2 x_{1} x_{2}$ 的值为.

查看试题解析
9. 如图，一个可以自由转动的圆形转盘被等分成6个相同的扇形区域，并涂上了相应的颜色，随机转动转盘，转盘停止时，指针恰好落在黄色区域的概率是.

查看试题解析
10. 在平面直角坐标系中，将函数 $y = 2 x^{2}$ 的图象先向右平移2个单位长度，再向上平移3个单位长度后，所得图象的函数表达式为.

查看试题解析
11. 用一个半径为10cm半圆纸片围成一个圆锥的侧面（接缝忽略不计），则该圆锥的高为 cm.

查看试题解析
12. 如图，在 $△ A B C$ 中， $D E // F G // B C$ ， $△ A D E$ 的面积＝梯形 $D F G E$ 的面积＝梯形 $F B C G$ 的面积，则 $\frac{D E}{B C}$ 的值为.

查看试题解析

13. 已知二次函数

y = a x^{2} + b x + c

（a、b、c是常数，且

a \neq 0

），函数值y与自变量x的部分对应值如下表：

$x$	…	$- 1$	0	1	2	3	4	…
$y$	…	10	$y_{1}$	2	1	2	5	…

当 $y < y_{1}$ 时，自变量x的取值范围是.

查看试题解析

14. 如图，在菱形 $A B C D$ 中，O是对角线 $B D$ 上一点， $⊙ O$ 经过点A，B，C，若 $⊙ O$ 的半径为2， $O D = 4$ ，则 $B C$ 的长为.

查看试题解析
15. 关于x的方程 $x^{2} - 2 x + m = p^{2}$ ，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为.

查看试题解析
16. 在 $△ A B C$ 中， $A B = A C = 10$ ， $B C = 12$ ，M，N是 $B C$ 边上两个动点，若 $A B$ ， $A C$ 边上分别存在点P，Q使得 $∠ M P N = ∠ M Q N = 60 °$ ，则线段 $M N$ 的最小值为.

查看试题解析

三、解答题

17. 解下列一元二次方程：

(1)、 $2 x^{2} - x - 1 = 0$ ；

(2)、 ${(2 x + 1)}^{2} = {(x - 1)}^{2}$ .

查看试题解析
18. 某校开展“垃圾分类，从我做起”的活动，该活动的志愿者从甲、乙、丙、丁四名同学中随机抽取.

(1)、若随机抽取1名，甲被抽中的概率为；

(2)、若随机抽取2名，求甲在其中的概率.

查看试题解析
19. 某中学九年级学生共进行了五次体育模拟测试，已知甲、乙两位同学五次模拟测试成绩的总分相同，小明根据甲同学的五次测试成绩绘制了尚不完整的统计表，并给出了乙同学五次测试成绩的方差的计算过程.
甲同学五次体育模拟测试成绩统计表

次数

第一次

第二次

第三次

第四次

第五次

成绩（分）

35

39

37

$a$

40

小明将乙同学五次模拟测试成绩直接代入方差公式，计算过程如下：

$S_{乙}^{2} = \frac{1}{5} [{(36 - 38)}^{2} + {(38 - 38)}^{2} + {(37 - 38)}^{2} + {(39 - 38)}^{2} + {(40 - 38)}^{2}] = 2 (分^{2})$

根据上述信息，完成下列问题：

(1)、a的值是；

(2)、根据甲、乙两位同学这五次模拟测试成绩，你认为谁的体育成绩更好？并说明理由；

(3)、如果甲再测试1次，第六次模拟测试成绩为38分，与前5次相比，甲6次模拟测试成绩的方差.（填“变大”“变小”或“不变”）

查看试题解析
20. 如图，四边形 $A B C D$ 是平行四边形，E是 $B A$ 延长线上的一点，连接 $E C$ 交 $A D$ 于点F.求证： $△ B E C ∽ △ D C F$ .

查看试题解析
21. 在平面直角坐标系中，二次函数的图象如图所示.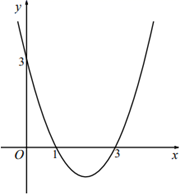

(1)、求该二次函数的表达式；

(2)、当 $- 1 < x < 3$ 时，则函数值y的取值范围为；

(3)、将该二次函数的图象向上平移个单位长度后恰好经过点 $(2 ， 0)$ .

查看试题解析
22. 如图， $P A$ 是 $⊙ O$ 的切线，A为切点，点B、C、D在 $⊙ O$ 上，且 $P A = P B$ .

(1)、求证： $P B$ 是 $⊙ O$ 的切线；

(2)、若 $∠ P = 100 °$ ，则 $∠ B + ∠ D$ 的度数为°.

查看试题解析
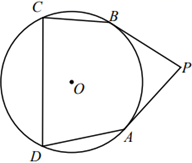23. 在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ，a、b、c为常数）的图象经过点 $A (1, 3)$ ， $B (- 1, - 1)$ .

(1)、 $b =$ ， $c =$ （用含有a的代数式表示）；

(2)、求证：不论a为何值，该函数图象与x轴总有两个不同的公共点.

查看试题解析
24. 如图，在 $△ A B C$ 中， $A D$ 是 $B C$ 边上的中线，E是 $A D$ 上一点， $∠ B E D = ∠ A B C$ .

(1)、求证： $D C^{2} = D E \cdot D A$ ；

(2)、若 $∠ B A C = 70 °$ ，则 $∠ B E C$ 的度数为°.

查看试题解析
25. 已知四边形 $A B C D$ ，用无刻度的直尺和圆规完成下列作图.（保留作图痕迹，不写作法）

(1)、如图①，连接 $B D$ ，在 $B C$ 边上作出一个点M，使得 $∠ A M D = ∠ A B D$ ；

(2)、如图②，在 $B C$ 边上作出一个点N，使得 $∠ A N D = ∠ A$ .

查看试题解析
26. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，弦 $A E$ 交 $B C$ 于点D，且 $\frac{A B}{A E} = \frac{A D}{A B}$ .

(1)、求证： $A B = A C$ ；

(2)、连接 $B O$ 并延长交 $A C$ 于点F，若 $A F = 4$ ， $C F = 5$ ，求 $⊙ O$ 的半径.

查看试题解析
27. 某公司销售一种服装，已知每件服装的进价为60元，售价为120元.为了促销，公司推出如下促销方案：如果一次购买的件数超过20件，那么每超出一件，每件服装的售价就降低2元，但每件服装的售价不得低于a元.该公司某次销售该服装所获得的总利润y（元）与购买件数x（件）之间的函数关系如图所示.

(1)、当 $x = 25$ 时，y的值为；

(2)、求a的值；

(3)、求y关于x的函数表达式；

(4)、若一次购买的件数x不超过m件，探索y的最大值，直接写出结论.（可以用含有m的代数式表示）

查看试题解析

次数	第一次	第二次	第三次	第四次	第五次
成绩（分）	35	39	37	$a$	40