江苏省南京市秦淮区2021届九年级上学期数学期末考试试卷

试卷更新日期：2021-03-30 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x^{2} = 0$ B、 $2 x^{3} - x = 0$ C、 $x y - 1 = 0$ D、 $\frac{1}{x^{2}} + x = 2$

查看试题解析
2. 下列随机事件：①在一副扑克牌中，抽一张是红桃；②抛掷一枚质地均匀的骰子，朝上一面是偶数；③抛一枚质地均匀的硬币，正面朝上；④不透明的袋子中有除颜色外完全相同的红球和白球各2个，摸出一个是白球，其中，概率为 $\frac{1}{2}$ 的是（）

A、①③ B、①②③ C、②③④ D、①②③④

查看试题解析
3. 圆锥的底面半径为2，母线长为4，则其侧面积为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $16 π$

查看试题解析
4. 某排球队6名场上队员的身高（单位：cm）是180，184，188，190，190，194.现用两名身高分别为185cm和188cm的队员换下场上身高为184cm和190cm的队员.与换人前相比，场上队员的身高（）

A、平均数变小，众数变小 B、平均数变小，众数变大 C、平均数变大，众数变小 D、平均数变大，众数变大

查看试题解析
5. 关于x的方程 $(x - 3) (x - 2) = p^{2}$ （p为常数）的根的情况，下列结论中正确的是（）

A、两个正根 B、两个负根 C、一个正根，一个负根 D、根的符号与p的值有关

查看试题解析
6. 已知四边形ABCD，下列命题：①若 $∠ A + ∠ C = 180 °$ ，则四边形ABCD一定存在外接圆；②若四边形ABCD内存在一点到四个顶点的距离相等，则 $∠ A + ∠ C = ∠ B + ∠ D$ ；③若四边形ABCD内存在一点到四条边的距离相等，则 $A B + C D = B C + A D$ ，其中，真命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

7. 方程x²﹣4＝0的解是．

查看试题解析
8. 若扇形的圆心角为60°，弧长为2π，则扇形的半径为．

查看试题解析
9. 将一元二次方程 $x^{2} - 3 x + 1 = 0$ 变形为 ${(x + h)}^{2} = k$ 的形式为.

查看试题解析

10. 甲、乙两名射击运动员在平时某练习中的成绩如下表：

甲的成绩					乙的成绩
环数	7	8	9	10	环数	7	8	9	10
频数	2	3	3	2	频数	4	6	6	4

则甲、乙两名射击运动员在该练习中成绩的方差 $S_{甲}^{2}$ 、 $S_{乙}^{2}$ 的大小关系为.

查看试题解析

11. 如图，在圆内接四边形ABCD中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 的度数之比为 $2 ： 4 ： 7$ ，则 $∠ D =$ .

查看试题解析
12. 如图，在平面直角坐标系中，一个圆经过 $O (0 ， 0)$ ， $A (3 ， 5)$ ， $B (6 ， 0)$ 三点，则该圆的圆心的坐标是.

查看试题解析
13. $α$ 是一元二次方程 $x^{2} - 2 x - 4 = 0$ 的一个根， $α + β = 2$ ，则 $β^{2} - 2 β$ 的值是.

查看试题解析
14. 某商店将进价为30元/件的文化衫以50元/件售出，每天可卖200件，在换季时期，预计单价每降低1元，每天可多卖10 件，则销售单价定为多少元时，商店可获利3000元？设销售单价定为x元/件，可列方程.（方程不需化简）

查看试题解析
15. 如图，在 $△ A B C$ 中， $A C = 3$ ， $B C = 4$ ， $A B = 5$ ， $∠ C A B$ 的平分线交弧ACB于点D，则AD的长是.

查看试题解析
16. 已知 $A B = 2 \sqrt{3}$ ，C是平面内一个动点， $60 ° \leq ∠ A C B \leq 120 °$ ，则满足条件的点C所在区域的面积是.

查看试题解析

三、解答题

17. 解方程： $x^{2} - 4 x = 0$ ．

查看试题解析
18.

(1)、解方程 $x + 2 = x^{2}$ ；

(2)、方程 $\sqrt{x + 2} = x$ 的解为.

查看试题解析
19. 已知关于x的方程 $x^{2} + 2 m x + m^{2} - 1 = 0$ .

(1)、求证：不论m为何值，该方程都有两个不相等的实数根；

(2)、若该方程的两个实数根在数轴上所对应的点关于原点对称，则m的值为.

查看试题解析
20. 如图所示，一块长方形铁皮的长是宽的2倍，四角各截去一个正方形，制成高是5cm，容积是500cm³的无盖长方体容器.求这块铁皮的长和宽.

查看试题解析
21. 圆周率 $π$ 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 $π$ 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 $π$ 的值.

(1)、对于边长为a的正方形，其外接圆半径为，根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 $C = 2 π r$ ，可以估算 $π = \frac{C}{2 r} =$ .

(2)、类比（1），当正多边形为正六边形时，估计 $π$ 的值.

查看试题解析
22. 九年级某班女生进行为期一周的仰卧起坐训练，下面两图是该班女生训练前后“1分钟仰卧起坐”测试的成绩统计图.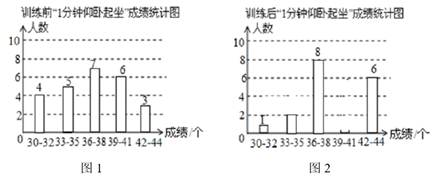

(1)、根据图1提供的信息，补全图2；

(2)、下列说法正确的是（填写所有正确的序号）
①训练前该班女生的平均成绩是 $\frac{31 \times 4 + 34 \times 5 + 37 \times 7 + 40 \times 6 + 43 \times 3}{25} = 36.88$ 个；

②比较训练前后的成绩，共有3个成绩段的人数变化最大；

③训练前后成绩的中位数所在的成绩段由“36~38”变为“39~41”.

查看试题解析
23. 小秋打算去某影城看电影.她用手机打开购票页面，座位已选情况如图所示（虚线边框内为黄金区域，其余为普通区域；深色为已售座位，白色为可选座位）.求下列事件的概率：

(1)、小秋独自观影，他选择第4排或第5排的概率是；

(2)、小秋约小叶一同观影，求小秋选择2个同排相邻的座位恰好都在黄金区域的概率.

查看试题解析
24. 在 $△ A B C$ 中， $A B = A C$ .

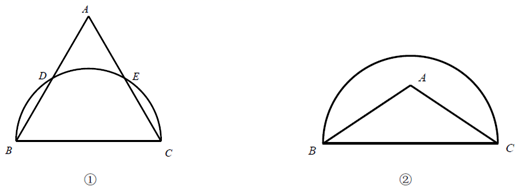(1)、如图①，点A在以BC为直径的半圆外，AB、AC分别与半圆交于点D、E，求证： $B D = E C$ ；

(2)、如图②，点A在以BC为直径的半圆内，请用无刻度的直尺在半圆上画出一点D，使得 $△ D B C$ 是等腰直角三角形（保留作图痕迹，不写画法）.

查看试题解析
25. 如图， $△ A B C$ 内接于⊙O，过点A作直线AD，使 $∠ C A D = ∠ A B C$ .

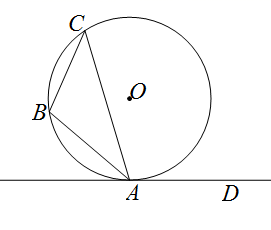(1)、求证：直线AD与⊙O相切.

(2)、若E是 $\overset{⌢}{A B}$ 的中点，连接OE并延长交直线AD于点F， $A B = 24$ ， $O F = 25$ ，则⊙O的半径是.

查看试题解析
26. 工厂2018年共生产4000万件电子产品，该年还生产了A、B、C三种型号的电池，其数量分别为400万块、800万块、1600万块，这些电池只配装了该年生产的部分电子产品（每一件电子产品配一块电池），剩余电子产品所需电池由其他工厂供给，从2019年起，该工厂逐年扩大这三种类型的电池产量.2019年、2020年这两年，A型电池每年产量的增长率相同，B型电池每年产量的增长率比A型电池每年产量的增长率小1，C型电池每年产量的增长率是A型电池每年产量的增长率的一半，已知该工厂2020年生产的三种类型的电池恰好配装了该年生产的所有电子产品，且该年生产的电子产品的数量是2018年生产的电子产品的数量的3.3倍，求A型电池每年产量的增长率.

查看试题解析
27. 数学概念
经过初中的数学学习，我们知道图形之间的距离总可以转化为两点之间的距离.一般地，P为图形A上任意一点，Q为图形B上任意一点，则称PQ长的最小值叫做图形A与图形B的距离，记作d（A，B）.

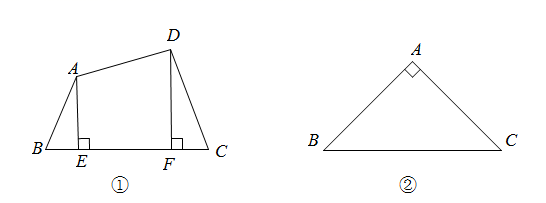(1)、概念理解
如图①，在四边形ABCD中， $A E ⊥ B C$ ， $D F ⊥ B C$ ，垂足分别为E、F，则d（AD，BC）是（）.

A、AB的长 B、AE的长 C、DF的长 D、DC的长

(2)、知识运用
如图②，在 $Rt △ A B C$ 中， $∠ A = 90 °$ ， $A B = A C = 4 \sqrt{2}$ ，P是平面内的一点， $P A = 3$ .

①直接写出d（P，BC）的取值范围；

②以P为圆心，1为半径作圆，当⊙P在 $△ A B C$ 的内部，且与其一边相切时，求⊙P与另两边的距离.

(3)、问题解决
如图③，某广场有一个边长为12m的菱形花坛，现准备绕着花坛铺设一条封闭的健身跑道，使靠近花坛的跑道内沿与花坛的距离为2m，则所铺设的健身跑道内沿的长度的最小值为m.

查看试题解析