河南省新乡市2020-2021学年高三下学期理数2月一轮复习摸底考试试卷
试卷更新日期:2021-03-29 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则( )A、 B、 C、 D、2. 设 , ,则 ( )A、6 B、5 C、4 D、33. 函数 的图象大致为( )A、
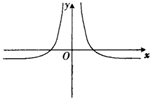 B、
B、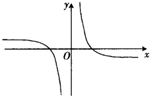 C、
C、 D、
D、 4. 某高中为了解学生课外知识的积累情况,随机抽取200名同学参加课外知识测试,测试共5道题,每答对一题得20分,答错得0分.已知每名同学至少能答对2道题,得分不少于60分记为及格,不少于80分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是( )
4. 某高中为了解学生课外知识的积累情况,随机抽取200名同学参加课外知识测试,测试共5道题,每答对一题得20分,答错得0分.已知每名同学至少能答对2道题,得分不少于60分记为及格,不少于80分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是( )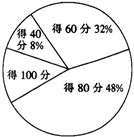 A、该次课外知识测试及格率为90% B、该次课外知识测试得满分的同学有30名 C、该次测试成绩的中位数大于测试成绩的平均数 D、若该校共有3000名学生,则课外知识测试成绩能得优秀的同学大约有1440名5. 已知向量 , ,则 在 方向上的投影为( )A、 B、 C、 D、6. 如图,在正三棱柱 中, , ,点 是侧棱 的中点,则直线 与平面 所成角的余弦值为( )
A、该次课外知识测试及格率为90% B、该次课外知识测试得满分的同学有30名 C、该次测试成绩的中位数大于测试成绩的平均数 D、若该校共有3000名学生,则课外知识测试成绩能得优秀的同学大约有1440名5. 已知向量 , ,则 在 方向上的投影为( )A、 B、 C、 D、6. 如图,在正三棱柱 中, , ,点 是侧棱 的中点,则直线 与平面 所成角的余弦值为( ) A、 B、 C、 D、7. 已知函数 的图象向右平移 个单位长度后,与函数 的图象重合,则 的单调递减区间为( )A、 B、 C、 D、8. 某几何体的三视图如图所示,其中俯视图中的半圆的直径为 ,则该几何体的表面积为( )
A、 B、 C、 D、7. 已知函数 的图象向右平移 个单位长度后,与函数 的图象重合,则 的单调递减区间为( )A、 B、 C、 D、8. 某几何体的三视图如图所示,其中俯视图中的半圆的直径为 ,则该几何体的表面积为( ) A、 B、 C、 D、9. 意大利数学家斐波那契于 年在他撰写的《算盘全书》中提出一个数列:1,1,2,3,5,8,13,21,34,…….这个数列称为斐波那契数列,该数列与自然界的许多现象有密切关系,在科学研究中有着广泛的应用.该数列 满足 , ,则该数列的前1000项中,为奇数的项共有( )A、333项 B、334项 C、666项 D、667项10. 已知抛物线 ,过点 的直线 交 于 , 两点,则直线 , ( 为坐标原点)的斜率之积为( )A、-8 B、-4 C、-2 D、-111. 已知数列 满足 , ,则数列 的前 项和 ( )A、 B、 C、 D、12. 已知定义域为 的函数 满足 ,且 , 为自然对数的底数,若关于 的不等式 恒成立,则实数 的取值范围为( )A、 B、 C、 D、
A、 B、 C、 D、9. 意大利数学家斐波那契于 年在他撰写的《算盘全书》中提出一个数列:1,1,2,3,5,8,13,21,34,…….这个数列称为斐波那契数列,该数列与自然界的许多现象有密切关系,在科学研究中有着广泛的应用.该数列 满足 , ,则该数列的前1000项中,为奇数的项共有( )A、333项 B、334项 C、666项 D、667项10. 已知抛物线 ,过点 的直线 交 于 , 两点,则直线 , ( 为坐标原点)的斜率之积为( )A、-8 B、-4 C、-2 D、-111. 已知数列 满足 , ,则数列 的前 项和 ( )A、 B、 C、 D、12. 已知定义域为 的函数 满足 ,且 , 为自然对数的底数,若关于 的不等式 恒成立,则实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 已知实数 满足 ,则 的最小值为.14. 小张计划从5个沿海城市和4个内陆城市中随机选择2个去旅游,则他至少选择1个沿海城市的概率是.15. 已知双曲线 的左、右焦点分别为 , ,点 在其右支上, 的内切圆为圆 , ,垂足为点 , 为坐标原点,则 .16. 定义在 上的函数 满足 ,当 时, .若不等式 对任意 恒成立,则实数 的最小值为.
三、解答题
-
17. 在 中, , , 分别为角 , , 的对边,且 .(1)、求角 ;(2)、若 的面积为 , 边上的高 ,求 , .18. 某射击小组由两名男射手与一名女射手组成,射手的每次射击都是相互独立的,已知每名男射手每次的命中率为 ,女射手每次的命中率为 .(1)、当每人射击2次时,求该射击小组共射中目标4次的概率;(2)、当每人射击 次时,规定两名男射手先射击,如果两名男射手都没有射中,那么女射手失去射击资格.一个小组共射中目标 次得100分,射中目标2次得60分,射中目标1次得10分,没有射中目标得-50分.用随机变量 表示这个射击小组的总得分,求 的分布列及数学期望.19. 点 , 分别是正方形 的边 , 的中点,点 在边 上,且 ,沿图 中的虚线 、 、 将 、 、 折起使 、 、 三点重合,重合后的点记为点 ,如图 .
 (1)、证明: ;(2)、求二面角 的余弦值.20. 已知动点 到点 的距离与到直线 的距离之比为 .(1)、求动点 的轨迹 的标准方程;(2)、过点 的直线 交 于 , 两点,已知点 ,直线 , 分别交 轴于点 , .试问在 轴上是否存在一点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、证明: ;(2)、求二面角 的余弦值.20. 已知动点 到点 的距离与到直线 的距离之比为 .(1)、求动点 的轨迹 的标准方程;(2)、过点 的直线 交 于 , 两点,已知点 ,直线 , 分别交 轴于点 , .试问在 轴上是否存在一点 ,使得 ?若存在,求出点 的坐标;若不存在,请说明理由.