河南省2021届高三下学期理数高考适应性考试试卷

试卷更新日期：2021-03-29 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ y = \lg (x + 3) + \lg (5 - x)}$ ， $B = {x ∣ x^{2} + x - 6 < 0}$ ，则 $∁_{A} B =$ （）

A、 $(- \infty ， - 3] \cup [2 ， + \infty)$ B、 $(- \infty - 3) \cup (2 ， + \infty)$ C、 $(2 ， 5)$ D、 $[2 ， 5)$

查看试题解析
2. 已知复数 $z$ 满足 $z (1 + i) = | 2 + 2 i |$ （其中 $i$ 为虚数单位），则复数 $z$ 的虚部为（）

A、 $\sqrt{2}$ B、 $- \sqrt{2}$ C、 $\sqrt{2} i$ D、 $- \sqrt{2} i$

查看试题解析
3. 若函数 $f (x) = \sin (x + φ) + 2 \cos x$ 的最大值为 $\sqrt{7}$ ，则常数 $φ$ 的一个可能取值为（）

A、 $- \frac{π}{6}$ B、 $- \frac{π}{3}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
4. 若实数 $x ， y ， z$ 满足 $\log_{2} x = \log_{3} y = 4^{x}$ ，则（）

A、 $x < y < z$ B、 $y < z < x$ C、 $z < x < y$ D、 $y < x < z$

查看试题解析
5. 如图，圆锥的轴截面ABC为正三角形，其面积为 $4 \sqrt{3}$ ，D为弧AB的中点，E为母线BC的中点，则异面直线 $A C ， D E$ 所成角的余弦值为（）

A、 $\frac{\sqrt{2}}{4}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
6. 已知点 $P$ 为抛物线 $x^{2} = 4 y$ 上任意一点，点 $A$ 是圆 $C ： x^{2} + {(y - 6)}^{2} = 5$ 上任意一点，则 $| P A |$ 的最小值为（）

A、 $6 - \sqrt{5}$ B、 $\sqrt{5}$ C、 $2 \sqrt{5}$ D、 $3 \sqrt{5}$

查看试题解析
7. “中国剩余定理”又称“孙子定理”，讲的是关于整除的问题.现有这样一个整除问题：将1到2021这2021个正整数中能被3除余1且被5除余1的数按从小到大的顺序排成一列，构成数列 ${a_{n}}$ ，则数列 ${a_{n}}$ 各项的和为（）

A、137835 B、137836 C、135809 D、135810

查看试题解析
8. 从正方体的12条棱中任选3条棱，则这3条棱两两异面的概率为（）

A、 $\frac{2}{55}$ B、 $\frac{3}{55}$ C、 $\frac{4}{55}$ D、 $\frac{5}{55}$

查看试题解析
9. 若 $△ A B C$ 的外心为 $O$ ，且 $∠ A = 60 ° ， A B = 2 ， A C = 3$ ，则 $\vec{O A} \cdot \vec{B A} + \vec{O B} \cdot \vec{C B} + \vec{O C} \cdot \vec{A C}$ 等于（）

A、5 B、8 C、10 D、13

查看试题解析
10. 若函数 $f (x) = x - 1 + a e^{1 - x}$ （ $a$ 为常数）存在两条均过原点的切线，则实数 $a$ 的取值范围是（）

A、 $(0 ， \frac{1}{e})$ B、 $(\frac{1}{e} ， + \infty)$ C、 $(0 ， e)$ D、 $(e ， + \infty)$

查看试题解析
11. 棱长为4的正方体密闭容器内有一个半径为1的小球，小球可在正方体容器内任意运动，则其不能到达的空间的体积为（）

A、 $32 - \frac{22}{3} π$ B、 $48 - 12 π$ C、 $28 - \frac{4}{3} π$ D、 $20 - \frac{13}{3} π$

查看试题解析

二、多选题

12. 我国新冠肺炎疫情进入常态化，各地有序推进复工复产，下面是某地连续11天复工复产指数折线图，下列说法正确的是（）

A、这11天复工指数和复产指数均逐日增加； B、这11天期间，复产指数增量大于复工指数的增量； C、第3天至第11天复工复产指数均超过80%； D、第9天至第11天复产指数增量大于复工指数的增量；

查看试题解析

三、填空题

13. 已知 ${\begin{array}{l} x + y - 2 ⩽ 0 ， \\ x - y - 2 ⩽ 0 ， \\ 2 x - y + 2 ⩾ 0 ， \end{array}$ 则 $z = x - 2 y$ 的最大值为．

查看试题解析
14. 函数 $f (x) = \frac{\sin π x}{x^{2} - x + 1}$ 的最大值为.

查看试题解析
15. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右交点分别为 $F_{1} ， F_{2}$ ，点 $P$ 在双曲线上．若 $△ P F_{1} F_{2}$ 为直角三角形，且 $\tan ∠ P F_{1} F_{2} = \frac{5}{12}$ ，则双曲线的离心率为．

查看试题解析
16. 在数列 ${a_{n}}$ 中， $a_{1} = 1 ， a_{n + 1} = 3 a_{n} - 2^{n - 1} (n \in N^{*})$ ，记 $c_{n} = 3^{n} - 2 \times {(- 1)}^{n} λ a_{n}$ ，若对任意的 $n \in N^{*} ， c_{n + 1} > c_{n}$ 恒成立，则实数 $λ$ 的取值范围为.

查看试题解析

四、解答题

17. 在如图所示的空间几何体中，平面 $A C D ⊥$ 平面 $A B C$ ， $△ A C D$ 与 $△ A C B$ 均是等边三角形， $A C = B E = 4$ ， $B E$ 和平面 $A B C$ 所成的角为 $60 °$ ，且点 $E$ 在平面 $A B C$ 上的射影落在 $∠ A B C$ 的平分线上.

(1)、求证： $D E ⊥$ 平面 $A D C$ ；

(2)、求直线 $B A$ 与平面 $D A E$ 所成角的正弦值.

查看试题解析
18. 在① $\frac{\sqrt{3}}{3} c \sin B = a - b \cos C$ ，② $b \sin C = c \cos (B - \frac{π}{6})$ 这两个条件中任选一个作为已知条件，补充到下面的横线上并作答.
问题： $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，已知 .

(1)、求 $B$ ；

(2)、若 $D$ 为 $A C$ 的中点， $B D = 2$ ，求 $△ A B C$ 的面积的最大值.

查看试题解析

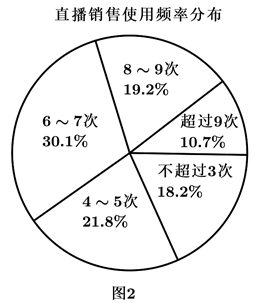
19. 直播带货是扶贫助农的一种新模式，这种模式是利用主流媒体的公信力，聚合销售主播的力量助力打通农产品产销链条，切实助力贫困地区农民脱贫增收．某贫困地区有统计数据显示，2020年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示，一周内使用直播销售的频率分布扇形图如图2所示．若将销售主播按照年龄分为“年轻人”（20岁~39岁）和“非年轻人”（19岁及以下或者40岁及以上）两类，将一周内使用的次数为6次或6次以上的称为“经常使用直播销售用户”，使用次数为5次或不足5次的称为“不常使用直播销售用户”，则“经常使用直播销售用户”中有

\frac{5}{6}

是“年轻人”．

参考数据：独立性检验临界值表

$P (K^{2} ⩾ k_{0})$	0.15	0.10	0.050	0.025	0.010
$k_{0}$	2.072	2.706	30841	5.024	6.635

其中， $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)} ， n = a + b + c + d$ ．

(1)、现对该地相关居民进行“经常使用网络直播销售与年龄关系”的调查，采用随机抽样的方法，抽取一个容量为200的样本，请你根据图表中的数据，完成

2 \times 2

列联表，并根据列联表判断是否有85%的把握认为经常使用网络直播销售与年龄有关？

使用直播销售情况与年龄列联表

	年轻人	非年轻人	合计
经常使用直播销售用户
不常使用直播销售用户
合计

(2)、某投资公司在2021年年初准备将1000万元投资到“销售该地区农产品”的项目上，现有两种销售方案供选择：

方案一：线下销售．根据市场调研，利用传统的线下销售，到年底可能获利30%，可能亏损15%，也可能不赔不赚，且这三种情况发生的概率分别为 $\frac{7}{10} ， \frac{1}{5} ， \frac{1}{10}$ ；

方案二：线上直播销售．根据市场调研，利用线上直播销售，到年底可能获利50%，可能亏损30%，也可能不赔不赚，且这三种情况发生的概率分别为 $\frac{3}{5} ， \frac{3}{10} ， \frac{1}{10}$ ．

针对以上两种销售方案，请你从期望和方差的角度为投资公司选择一个合理的方案，并说明理由．

查看试题解析

20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，直线 $l ： y = k x + a$ ，直线 $l$ 与椭圆 $C$ 交于 $M$ ， $N$ 两点，与 $y$ 轴交于点 $P$ ， $O$ 为坐标原点．

(1)、若 $k = 1$ ，且 $N$ 为线段 $M P$ 的中点，求椭圆 $C$ 的离心率；

(2)、若椭圆长轴的一个端点为 $Q (2 ， 0)$ ，直线 $Q M ， Q N$ 与 $y$ 轴分别交于 $A ， B$ 两点，当 $\vec{P A} \cdot \vec{P B} = 1$ 时，求椭圆 $C$ 的方程．

查看试题解析
21. 已知函数 $f (x) = a x^{2} - (6 + a) x + 3 \ln x$ .

(1)、当 $a \leq 0$ 时，讨论函数 $f (x)$ 的单调性；

(2)、当 $a \leq - \frac{9}{2}$ 时，关于 $x$ 的不等式 $f (x) + a x - b \geq 0$ 有解，求 $b$ 的最大值.

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = t \cos α ， \\ y = - 2 + t \sin α \end{array}$ （ $t \in R ， t$ 为参数 $α \in (0 ， \frac{π}{2})$ ）．以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，半圆 $C$ 的极坐标方程为 $ρ = 2 \sin θ ， θ \in (\frac{π}{4} ， \frac{3 π}{4})$ ．

(1)、求半圆 $C$ 的参数方程和直线 $l$ 的直角坐标方程；

(2)、直线 $l$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，点 $D$ 在半圆 $C$ 上，且直线 $C D$ 的倾斜角是直线 $l$ 的倾斜角的2倍， $△ A B D$ 的面积为 $1 + \sqrt{3}$ ，求 $α$ 的值．

查看试题解析
23. 已知 $a ， b ， c$ 是正实数，且满足 $a + \frac{b}{2} + \frac{c}{3} = 1$ ．

(1)、是否存在满足已知条件的 $a ， b$ ，使得 $a b = \frac{1}{2}$ ，试说明理由；

(2)、求 $\sqrt{a} + \sqrt{b} + \sqrt{c}$ 的最大值．

查看试题解析