重庆市沙坪坝区南开学区共同体2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-29 类型：开学考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、 $\pm 2$ B、 $\sqrt{2}$ C、 $2$ D、 $- 2$

查看试题解析
2. 计算 ${(2 x)}^{3}$ 的结果是（）

A、 $2 x^{3}$ B、 $6 x$ C、 $8 x^{3}$ D、 $6 x^{3}$

查看试题解析
3. 以下列各组数据为边长作三角形，其中能组成直角三角形的是( )

A、2，3，4 B、3，5，7 C、4，6，8 D、6，8，10

查看试题解析
4. 估算 $\sqrt{19} + 2$ 的结果在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
5. 如图，在 $O A$ ， $O B$ 上分别截取 $O D$ ， $O E$ ，使 $O D = O E$ ，再分别以点 $D$ ， $E$ 为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ A O B$ 内交于点 $C$ ，作射线 $O C$ ， $O C$ 就是 $∠ A O B$ 的角平分线．这是因为连 $C D$ ， $C E$ ，可得到 $Δ C O D ≌ Δ C O E$ ，根据全等三角形对应角相等，可得 $∠ C O D = ∠ C O E$ ．在这个过程中，得到 $Δ C O D ≌ Δ C O E$ 的条件是（）

A、SAS B、AAS C、ASA D、SSS

查看试题解析
6. 一个长方形操场，面积为 $3 a^{2} b + 6 a$ ，其中一边长为 $3 a$ ，则另一边长为（）

A、 $a b + 2$ B、 $a b + 2 a$ C、 $a + 2$ D、 $a^{2} b + a$

查看试题解析
7. 下列说法正确的是（）

A、周长相等的两个三角形全等 B、面积相等的两个三角形全等 C、三个角对应相等的两个三角形全等 D、三条边对应相等的两个三角形全等

查看试题解析
8. 2020年新冠肺炎疫情影响全球，各国感染人数持续攀升，医用口罩供不应求，很多企业纷纷加入生产口罩的大军中来，重庆某企业临时增加甲、乙两个厂房生产口罩，甲厂房每天生产的数量是乙厂房每天生产数量的2倍，两厂房各加工6000箱口罩，甲厂房比乙厂房少用5天.设乙厂房每天生产x箱口罩.根据题意可列方程为（）

A、 $\frac{6000}{x} - \frac{6000}{2 x} = 5$ B、 $\frac{6000}{2 x} - \frac{6000}{x} = 5$ C、 $\frac{6000}{x} - \frac{6000}{x + 2} = 5$ D、 $\frac{6000}{x + 2} - \frac{6000}{x} = 5$

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C$ ，D为BC的中点， $A D = A E$ ，若 $∠ B A D = 40 °$ ，则 $∠ C D E$ 的度数为（）

A、 $10 °$ B、 $20 °$ C、 $30 °$ D、 $40 °$

查看试题解析
10. 已知 $a + b = 5$ ， $a b = - 2$ ，则 $a^{2} - a b + b^{2}$ 的值是（）

A、30 B、31 C、32 D、33

查看试题解析
11. 《九章算术》是我国古代最重要的数学著作之一，它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈，末折抵地，去本四尺，问折者高几何？”翻译成数学问题是：如图所示， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C + A B = 10$ 尺， $B C = 4$ 尺，求AC的长.则AC的长为（）

A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺

查看试题解析
12. 若关于x的分式方程 $\frac{m}{1 - x} = \frac{3}{x - 1} - 2$ 有非负实数解，且关于x的不等式组 ${\begin{array}{l} x + 1 \geq 0 \\ x + m \leq 2 \end{array}$ 有解，则满足条件的所有整数m的和为（）

A、 $- 9$ B、 $- 8$ C、 $- 7$ D、 $- 6$

查看试题解析

二、填空题

13. 新冠病毒的平均直径大约是0.00000014米，呈圆形或者椭圆形，主要通过呼吸道进行传播.将0.00000014用科学记数法表示为.

查看试题解析
14. 若分式 $\frac{x - 1}{x^{2} + 3}$ 的值为零，则 $x =$ .

查看试题解析
15. 因式分解2x²y﹣8y＝．

查看试题解析
16. 某校开展了“科技托起强国梦”征文活动，该校对初二年级六个班上交征文的篇数进行了统计，绘制了如图所示的折线统计图，则1班上交征文篇数的频率是.

查看试题解析
17. 如图，在 $△ A B C$ 中、 $∠ C = 90 °$ ，BE平分 $∠ A B C$ 交AC于点E. $E D ⊥ A B$ 、垂足为D、若 $B C = 8$ ， $A B = 17$ ，则 $△ A D E$ 的周长为.

查看试题解析
18. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D是边BC上任意一点，连结AD，过点C作 $C E ⊥ A D$ 于点E，过点C作 $C F ⊥ C E$ ，且 $C F = C E$ ，连结FE并延长交AB于点M，连结BF.若四边形AMEC的面积是8， $C E = 2$ ，则四边形ABFC的面积是.

查看试题解析

三、解答题

19. 计算：

(1)、 ${(2020 - π)}^{0} + {(\frac{1}{2})}^{- 2} + \sqrt[3]{- 8}$ ；

(2)、 $\sqrt{6} \times \sqrt{3} - \sqrt{24} \div \sqrt{3}$ .

查看试题解析
20. 如图，点 $B 、 E 、 C 、 F$ 在一条直线上， $A B = D E$ ， $A B$ ∥ $D E$ ， $B E = C F$ .

(1)、求证： $A C = D F$

(2)、若 $∠ D = 65$ °，求 $∠ E G C$ 的大小.

查看试题解析
21.

(1)、计算 ${(x - 2 y)}^{2} - x (x - 2 y)$ ；

(2)、 $\frac{3}{2 x} = \frac{2}{x + 1}$ .

查看试题解析
22. 为了解居民对垃圾分类相关知识的知晓程度（A.非常了解，B.了解，C.基本了解，D.不太了解），东东随机调查了若干人（每人必选且只能选择四种程度中的一种）.根据调查结果绘制成如图两幅不完整的统计图.请根据图中信息，解答下列问题：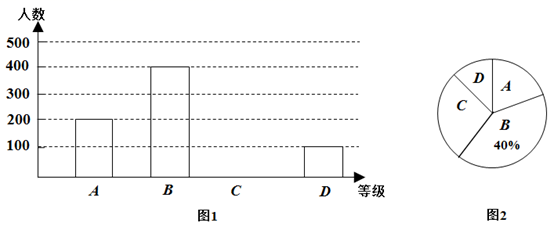

(1)、此次调查的总人数是人，对垃圾分类相关知识非常了解的人数所占的百分比为，对垃圾分类相关知识基本了解的人数在扇形统计图中所对应的圆心角的度数为；

(2)、请将条形统计图补充完整.

查看试题解析
23. 先化简，再求值： $(2 - \frac{2}{a + 1}) - \frac{2 a - 4}{a^{2} - 1} \div \frac{a - 2}{a^{2} - 2 a + 1}$ ；其中 $a = - 3$ .

查看试题解析
24. 如图，小区有一块三角形空地ABC，为响应沙区创文创卫，美化小区的号召，小区计划将这块三角形空地进行新的规划，过点D作垂直于AB的小路DE.经测量， $A B = 15$ 米， $A C = 13$ 米， $A D = 12$ 米， $D C = 5$ 米.

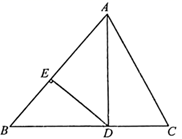(1)、求BD的长；

(2)、求小路DE的长.

查看试题解析
25. 若一个三位或三位以上的整数A分成左、中、右三个数后满足：①中间数=左边数²-右边数² ，则称中间数是A的“吉祥数”.如231的“吉祥数”是3，4122的“吉样数”是12；②中间数=（左边数-右边数）² ，则称中间数是A的“如意数”.如143的“如意数”是4，5161和1165的“如意数”是16.

(1)、若一个三位数的“吉祥数”是5，则这个数是，若一个四位数的“如意数”是81，则这个数是，

(2)、一个“吉祥数”与一个“如意数”的左边数均为m，右边数均为n，且这个“吉祥数”比这个“如意数”大12，求满足条件的“吉样数”.

查看试题解析
26. 如图，在 $△ A B C$ 中， $∠ A C B = 90 ° A C = B C$ ，点D是线段BC边上的一点，连结AD，点E在射线BC上，过E作 $E F ⊥ A D$ 交AD于点F.

(1)、如图1，当D是BC的中点，且 $D F = B D$ 时，若 $A B = 4 \sqrt{2}$ ，求CE的长；

(2)、如图2，当 $C E = C D$ 时，延长EF交AB于点G，取AD的中点H，连结EH，过点A作 $A M / / B E$ ，交EH的延长线于点M，猜想AM与BG之间的数量关系并证明.

查看试题解析