重庆市开州区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-29 类型:期末考试
一、单选题
-
1. 下列长度的线段能组成三角形的是( )A、2,3,5 B、4,6,11 C、5,8,10 D、4,8,42. 下列银行标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 要使分式 有意义,则 的取值应满足( )A、 B、 C、 且 D、4. 计算 的结果为( )A、 B、 C、 D、5. 以下四种作 边AC上的高,其中正确的作法是( )A、
3. 要使分式 有意义,则 的取值应满足( )A、 B、 C、 且 D、4. 计算 的结果为( )A、 B、 C、 D、5. 以下四种作 边AC上的高,其中正确的作法是( )A、 B、
B、 C、
C、 D、
D、 6. 下列说法不正确的是( ).A、两边和它们的夹角分别相等的两个三角形全等 B、两角分别相等且其中一组等角的对边相等的两个三角形全等 C、底边和顶角分别相等的两个等腰三角形全等 D、两边和其中一边的对角分别相等的两个三角形全等7. 若把分式 中的 、 都扩大为原来的3倍,则分式的值( )A、缩小3倍 B、扩大3倍 C、扩大9倍 D、不变8. 《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多1天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为 天,则可列方程为( )A、 B、 C、 D、9. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
6. 下列说法不正确的是( ).A、两边和它们的夹角分别相等的两个三角形全等 B、两角分别相等且其中一组等角的对边相等的两个三角形全等 C、底边和顶角分别相等的两个等腰三角形全等 D、两边和其中一边的对角分别相等的两个三角形全等7. 若把分式 中的 、 都扩大为原来的3倍,则分式的值( )A、缩小3倍 B、扩大3倍 C、扩大9倍 D、不变8. 《九章算术》中记录的一道题目译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多1天,如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为 天,则可列方程为( )A、 B、 C、 D、9. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )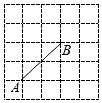 A、4 B、5 C、6 D、710. 如图, 中,将 沿 翻折,若 , ,则 多少度( )
A、4 B、5 C、6 D、710. 如图, 中,将 沿 翻折,若 , ,则 多少度( )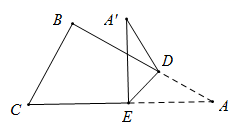 A、60° B、75° C、85° D、90°11. 如图是由“○”组成的龟图,则第10个龟图中“○”的个数是( )
A、60° B、75° C、85° D、90°11. 如图是由“○”组成的龟图,则第10个龟图中“○”的个数是( )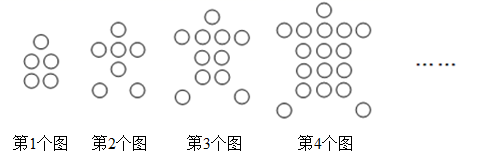 A、77 B、90 C、95 D、11612. 如果关于 的分式方程 有正整数解,且关于 的不等式组 至少有两个整数解,则满足条件的整数 的和为( )A、2 B、3 C、6 D、11
A、77 B、90 C、95 D、11612. 如果关于 的分式方程 有正整数解,且关于 的不等式组 至少有两个整数解,则满足条件的整数 的和为( )A、2 B、3 C、6 D、11二、填空题
-
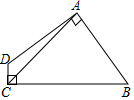
13. 随着电子技术的不断进步,电子元件的尺寸大幅缩小,电脑芯片上某电子元件大约只有0.000000645mm2 , 这个数用科学记数法表示为mm2.14. 计算: .15. 分解因式: .16. 如图,四边形ABCD中,AB=AD,AC=6,∠DAB=∠DCB=90°,则四边形ABCD的面积为.
 17. 如图,在四边形 中, , ,在直线 , 上分别找一点 , ,使得 的周长最小时,则 的度数为.
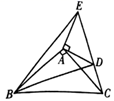
17. 如图,在四边形 中, , ,在直线 , 上分别找一点 , ,使得 的周长最小时,则 的度数为.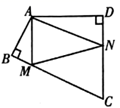 18. 如图,在 和 中, , , ,其中点 , , 在同一条直线上,连接 , .以下四个结论:
18. 如图,在 和 中, , , ,其中点 , , 在同一条直线上,连接 , .以下四个结论:① ;② ;③ ;④ .一定正确的是.
三、解答题
-
19. 计算:(1)、化简:(2)、因式分解:20. 如图,点 , , , 四点共线,且 , , .
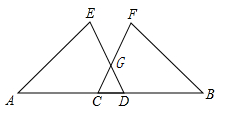 (1)、求证: ;(2)、若 , ,求线段 的长.21. 解答下面两题:(1)、解方程:(2)、化简:22. 如图,在 中, 和 的平分线相交于点 ,根据下列条件,求 的度数.
(1)、求证: ;(2)、若 , ,求线段 的长.21. 解答下面两题:(1)、解方程:(2)、化简:22. 如图,在 中, 和 的平分线相交于点 ,根据下列条件,求 的度数. (1)、若 , ,则 ;(2)、若 ,则 ;(3)、若 ,则 ;(4)、从以上的计算中,你能发现已知 ,求 的公式是: (提示:用 表示).23. 今年双11期间开州区紫水豆干凭借过硬的质量、优质的口碑大火,豆干店的王老板用2500元购进一批紫水豆干,很快售完;王老板又用4400元购进第二批紫水豆干,所购数量是第一批的2倍,由于进货量增加,进价比第一批每千克少了3元.(1)、第一批紫水豆干每千克进价多少元?(2)、该老板在销售第二批紫水豆干时,售价在第二批进价的基础上增加了 ,售出80%后,为了尽快售完,决定将剩余紫水豆干在第二批进价的基础上每千克降价 元进行促销,结果第二批紫水豆干的销售利润为1520元,求 的值.(利润=售价-进价)24. 已知在 中, 的平分线 与 的垂直平分线 交于点 , 于 , 交 的延长线于 .
(1)、若 , ,则 ;(2)、若 ,则 ;(3)、若 ,则 ;(4)、从以上的计算中,你能发现已知 ,求 的公式是: (提示:用 表示).23. 今年双11期间开州区紫水豆干凭借过硬的质量、优质的口碑大火,豆干店的王老板用2500元购进一批紫水豆干,很快售完;王老板又用4400元购进第二批紫水豆干,所购数量是第一批的2倍,由于进货量增加,进价比第一批每千克少了3元.(1)、第一批紫水豆干每千克进价多少元?(2)、该老板在销售第二批紫水豆干时,售价在第二批进价的基础上增加了 ,售出80%后,为了尽快售完,决定将剩余紫水豆干在第二批进价的基础上每千克降价 元进行促销,结果第二批紫水豆干的销售利润为1520元,求 的值.(利润=售价-进价)24. 已知在 中, 的平分线 与 的垂直平分线 交于点 , 于 , 交 的延长线于 .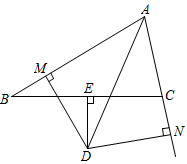 (1)、证明: ;(2)、当 时,求 的度数.25. 阅读材料:若 ,求 、 的值.
(1)、证明: ;(2)、当 时,求 的度数.25. 阅读材料:若 ,求 、 的值.,
,
,
, .
根据你的观察,探究下面的问题:
(1)、已知一个三角形的三边长分别为 、 、 ,且 、 、 都是正整数,并满足: ,则 .(2)、已知 、 、 是 的三边长,且满足 ,试判断 的形状.(3)、试探究关于 、 的代数式 是否有最小值,若存在,求出最小值及此时 、 的值;若不存在,说明理由.26. 在平面直角坐标系中,点 在 轴正半轴上,以 为边在 轴上方作等边 .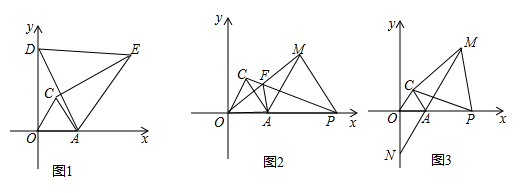 (1)、如图1,在 的右上方作线段 ,点 在 轴正半轴上, ,以 为边在 右侧作等边 ,则 .(2)、如图2,点 是 轴正半轴上且在点 右侧的一动点, 为等边三角形, 与 交于点 .
(1)、如图1,在 的右上方作线段 ,点 在 轴正半轴上, ,以 为边在 右侧作等边 ,则 .(2)、如图2,点 是 轴正半轴上且在点 右侧的一动点, 为等边三角形, 与 交于点 .求证: .
(3)、如图3,点 是 轴正半轴上且在点 右侧的一动点, 为等边三角形, 的延长线交 轴于点 ,请直接写出线段 、 、 的数量关系.