浙江省杭州市拱墅区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-29 类型:期末考试
一、单选题
-
1. 若点A的坐标为 ,则点A关于y轴的对称点的坐标为( )A、 B、 C、 D、2. 若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )A、1cm B、2cm C、5cm D、8cm3. 对于命题“ (a为实数)”,能说明它是假命题的反例是( )A、 B、 C、 D、4. 根据数量关系“y与6的和不小于1”列不等式,正确的是( )A、 B、 C、 D、5. 在三角形中,一定能将其面积分成相等两部分的是( )A、中线 B、高线 C、角平分线 D、某一边的垂直平分线6. 若实数a,b满足 ,则( )A、 B、 C、 D、7. 若一次函数 (k是常数, )的图象经过点P,且函数y的值随自变量x的增大而减小,则点P的坐标可以是( )A、 B、 C、 D、8. 如图,在 中,点D在边BC上,且满足 ,过点D作 ,交AC于点E.设 , , ,则( )
 A、 B、 C、 D、9. 已知一次函数 (k,b是常数, )若 ,则它的图象可能是( )A、
A、 B、 C、 D、9. 已知一次函数 (k,b是常数, )若 ,则它的图象可能是( )A、 B、
B、 C、
C、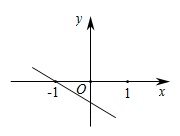 D、
D、 10. 在 中,已知 ,AD是 的角平分线, 于点E.若 的面积为S,则 的面积为( )A、 B、 C、 D、
10. 在 中,已知 ,AD是 的角平分线, 于点E.若 的面积为S,则 的面积为( )A、 B、 C、 D、二、填空题
-
11. 一张小凳子的结构如图所示, ,若 ,则 的度数为.
 12. 若B地在A地的南偏东30°方向,距离A地30km处,则A地在B地的方向,距离B地km处.13. 在 中, , , ,则线段AC的长为.14. 一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了道题.15. 如图,在 中, ,AD平分 ,PD垂直平分AB连接BD并延长,交边AC于点E.若 是等腰三角形,则 的度数为.
12. 若B地在A地的南偏东30°方向,距离A地30km处,则A地在B地的方向,距离B地km处.13. 在 中, , , ,则线段AC的长为.14. 一次生活常识知识竞赛一共有30道题,答对一题得4分,不答得0分,答错扣2分.小聪有2道题没答,竞赛成绩超过80分,则小聪至多答错了道题.15. 如图,在 中, ,AD平分 ,PD垂直平分AB连接BD并延长,交边AC于点E.若 是等腰三角形,则 的度数为. 16. 小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的 米, 分.
16. 小明和小杰在同一直道的A,B两点间作匀速往返走锻炼(忽略掉头等时间).小明从A地出发,同时小杰从B地出发,两人第一次相遇时小明曾停下接电话数分钟.图中的折线表示从开始到小杰第一次到达A地止,两人之间的距离y(米)与行走时间x(分)的函数关系图象.则图中的 米, 分.
三、解答题
-
17. 如图, 的顶点都在格点上,已知点C的坐标为 .
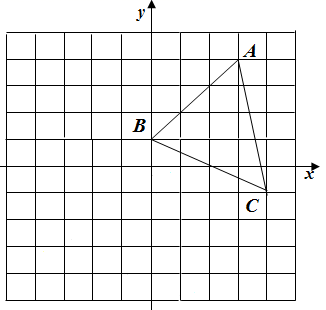
( 1 )写出点A,B的坐标;
( 2 )平移 ,使点A与点O重合.作出平移后的 ,并写出点 , 的坐标.
18. 解下列一元一次不等式(组):(1)、 ,并把它的解表示在数轴上.(2)、 .19. 如图,AC与BD相交于点O,且 , .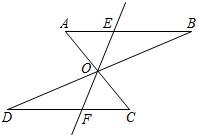 (1)、求证: ;(2)、直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.20. 在平面直角坐标系中,一次函数 (k,b是常数,且 )的图象经过点 和 .(1)、求该函数的表达式;(2)、若点 在该函数的图象上,求点P的坐标;(3)、当 时,求x的取值范围.21. 如图,在 中, ,D为CA延长线上一点, 于点E,交AB于点F.
(1)、求证: ;(2)、直线EF过点O,分别交AB,CD于点E,F,试判断OE与OF是否相等,并说明理由.20. 在平面直角坐标系中,一次函数 (k,b是常数,且 )的图象经过点 和 .(1)、求该函数的表达式;(2)、若点 在该函数的图象上,求点P的坐标;(3)、当 时,求x的取值范围.21. 如图,在 中, ,D为CA延长线上一点, 于点E,交AB于点F. (1)、求证: 是等腰三角形;(2)、若 , ,求线段DE的长.
(1)、求证: 是等腰三角形;(2)、若 , ,求线段DE的长.
