初中数学浙教版七年级下册第三章整式的乘除章末检测（提高训练）

试卷更新日期：2021-03-28 类型：单元试卷

进入出卷网下载

一、单选题

1. 若x ， y为正整数，且2^x•2^y=2⁵ ，则x ， y的值有（　　）

A、4对 B、3对 C、2对 D、1对

查看试题解析
2. 计算 ${(- 0.25)}^{2007} \times {(- 4)}^{2008}$ 等于（）.

A、 $- 1$ B、 $1$ C、 $- 4$ D、 $4$

查看试题解析
3. 已知 $a = 81^{31}$ ， $b = 27^{41}$ ， $c = 9^{61}$ ，则a、b、c的大小关系是（）

A、 $a > c > b$ B、 $a > b > c$ C、 $c > b > a$ D、 $b > c > a$

查看试题解析
4. 要使（﹣6x³）（x²+ax﹣3）的展开式中不含x⁴项，则a＝（）

A、1 B、0 C、﹣1 D、 $\frac{1}{6}$

查看试题解析
5. 已知（x﹣2）（x²+mx+n）的乘积项中不含x²和x项，则m ， n的值分别为（）

A、m＝2，n＝4 B、m＝3，n＝6 C、m＝﹣2，n＝﹣4 D、m＝﹣3，n＝﹣6

查看试题解析
6. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1)$ 的计算结果的个位数字是（）

A、8 B、6 C、2 D、0

查看试题解析
7. 已知2ⁿ＋2¹²＋1（n＜0）是一个有理数的平方，则n的值为（）

A、﹣16 B、﹣14 C、﹣12 D、﹣10

查看试题解析
8. 芝麻的用途广泛，经测算，一粒芝麻约有0. 00000201千克. 数据0. 00000201用科学记数法表示为（）

A、 $0.201 \times 10^{- 5}$ B、 $2.01 \times 10^{- 5}$ C、 $2.01 \times 10^{- 6}$ D、 $20.1 \times 10^{- 7}$

查看试题解析
9. 若 $3^{x} + 3^{x} + 3^{x} + 3^{x} = \frac{4}{9}$ ，则 $x =$ （）

A、-2 B、-1 C、0 D、 $\frac{1}{4}$

查看试题解析
10. 已知a，b，c为非零的实数，则 $\frac{a}{| a |} + \frac{a b}{| a b |} + \frac{a c}{| a c |} + \frac{b c}{| b c |}$ 的可能值的个数为（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 已知2^a＝5，2^b＝10，2^c＝100，那么a、b、c之间满足的等量关系是．

查看试题解析
12. 若单项式 $- 6 x^{2} y^{m}$ 与 $\frac{1}{3} x^{n - 1} y^{3}$ 是同类项，那么这两个单项式的积是.

查看试题解析
13. 设实数 $x, y, z$ 满足 $x^{2} + y^{2} + z^{2} - x y - y z - z x = 27$ ，则 $| y - z |$ 的最大值为.

查看试题解析
14. 若（t-3）^t-2=1，则t=.

查看试题解析
15. 已知 $6^{x} = 192$ ， $32^{y} = 192$ ，则 ${[(x - 1) (1 - y)]}^{2019} =$ .

查看试题解析
16. 已知整数a，b满足（ $\frac{2}{9}$ ）^a•（ $\frac{3}{4}$ ）^b=8，则a﹣b= ．

查看试题解析

三、解答题

17.

(1)、计算： $a \cdot a^{5} + {(2 a^{2})}^{3} - 2 a \cdot (3 a^{5} - 4 a^{3} + a) - {(- 2 a^{3})}^{2}$ ；

(2)、已知n是正整数，且 $x^{3 n} = 2$ ，求 ${(3 x^{3 n})}^{3} + {(- 2 x^{2 n})}^{3}$ 的值．

查看试题解析
18.

(1)、计算下列各式，并寻找规律：
① $1 - \frac{1}{2^{2}}$ =（_+_）（_-_）=

② $1 - \frac{1}{3^{2}}$ =（_+_）（_-_）=_；

(2)、运用（1）中所发现的规，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) (1 - \frac{1}{5^{2}})$ ;

(3)、猜想 $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{9^{2}}) (1 - \frac{1}{10^{2}}) \dots (1 - \frac{1}{n^{2}})$ 的结果，并写出推理过程.

查看试题解析
19. 已知 $a = \frac{1}{3} m + 2015$ ， $b = \frac{1}{3} m + 2016$ ， $c = \frac{1}{3} m + 2017$ ，求 $a^{2} + b^{2} + c^{2} - a b - b c - a c$ 的值．

查看试题解析
20. 某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：
①第一次提价p%，第二次提价q%；

②第一次提价q%，第二次提价p%；

③第一、二次提价均为 $\frac{p + q}{2} %$ .

其中p，q是不相等的正数，三种方案哪种提价最多？

查看试题解析
21. 基本事实：若 $a^{m} = a^{n}$ （a>0，且a≠1，m ， n都是正整数），则m=n.试利用上述基本事实解决下面的两个问题：

(1)、如果 $2 \times 8^{x} \times 16^{x} = 2^{22}$ ，求x的值．

(2)、如果 $2^{x + 1} • 2 + 2^{x + 1} = 24$ ，求x的值．

查看试题解析
22. 长方形的长为 $a$ 厘米，宽为 $b$ 厘米，其中 $a > b$ ，如果将原长方形的长和宽各增加3厘米，得到的新长方形面积记为 $S_{1}$ ，如果将原长方形的长和宽分别减少2厘米，得到的新长方形面积记为 $S_{2}$ ．

(1)、若 $a$ 、 $b$ 为正整数，请说明： $S_{1}$ 与 $S_{2}$ 的差一定是5的倍数；

(2)、如果 $S_{1} = 2 S_{2}$ ，求将原长方形的长和宽分别减少7厘米后得到的新长方形面积．

查看试题解析
23. 配方法是数学中重要的一种思想方法．它是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
我们定义：一个整数能表示成a²+b²（a，b是整数）的形式，则称这个数为“完美数”，例如，5是“完美数”．理由是：因为5＝1²+2²、所以5是“完美数”．

(1)、解决问题：
①已知29是“完美数”．请将它写成a²+b²（a、b是整数）的形式．

②若x²-4x+5可配方成（x-m）²+n（m，n为常数），则mn的值．

(2)、探究问题：
①已知x²+y²-2x+4y+5＝0，求x+y的值．

②已知S＝x²+4y²+4x-12y+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．

查看试题解析
24. 如图，将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形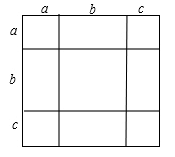

(1)、若用不同的方法计算这个边长为(a+b+c)的正方形面积，就可以得到一个等式，这个等式可以为 .(只要写出一个即可)

(2)、请利用(1)中的等式解答下列问题：
①若三个实数a，b，c满足a+b+c=11，ab+bc+ac=38，求a²+b²+c²的值

②若三个实数x，y，z满足2^x×4^y÷8^z= $\frac{1}{4}$ ，x²+4y²+9z²=44，求2xy-3xz-6yz的值

查看试题解析

初中数学浙教版七年级下册第三章 整式的乘除 章末检测（提高训练）

一、单选题

二、填空题

三、解答题

初中数学浙教版七年级下册第三章整式的乘除章末检测（提高训练）