初中数学浙教版八年级下册第三章数据分析初步章末检测（提高训练）

试卷更新日期：2021-03-27 类型：单元试卷

进入出卷网下载

一、单选题

1. 某校航模兴趣小组共有 30 位同学，他们的年龄分布如下表：

年龄/岁

13

14

15

16

人数

5

15

由于表格污损，15 岁和 16 岁的人数看不清，则下列关于年龄的统计量可以确定的是（）

A、平均数、中位数 B、众数、中位数 C、平均数、方差 D、中位数、方差

查看试题解析
2. 在对一组样本数据进行分析时，小华列出了方差的计算公式：s²＝ $\frac{{(2 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(3 - \bar{x})}^{2} + {(4 - \bar{x})}^{2}}{n}$ ，由公式提供的信息，则下列说法错误的是（）

A、样本的容量是4 B、样本的中位数是3 C、样本的众数是3 D、样本的平均数是3.5

查看试题解析
3. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析
4.
为了节约水资源，某市准备按照居民家庭年用水量实行阶梯水价．水价分档递增，计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%，15%和5%，为合理确定各档之间的界限，随机抽查了该市5万户居民家庭上一年的年用水量（单位：m³），绘制了统计图．如图所示，下面四个推断（　　）
①年用水量不超过180m³的该市居民家庭按第一档水价交费；
②年用水量超过240m³的该市居民家庭按第三档水价交费；
③该市居民家庭年用水量的中位数在150﹣180之间；
④该市居民家庭年用水量的平均数不超过180．

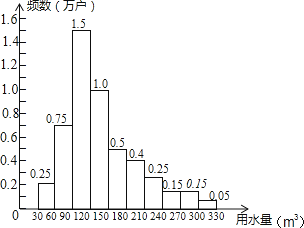A、①③ B、①④ C、②③ D、②④

查看试题解析
5. 某一公司共有51名员工（包括经理），经理的工资高于其他员工的工资，今年经理的工资从去年的200000元增加到225000元，而其他员工的工资同去年一样，这样，这家公司所有员工今年工资的平均数和中位数与去年相比将会（）

A、平均数和中位数不变 B、平均数增加，中位数不变 C、平均数不变，中位数增加 D、平均数和中位数都增大

查看试题解析
6. 若样本x₁+1，x₂+1，…，x_n+1的平均数为10，方差为2，则对于样本x₁+2，x₂+2，…，x_n+2，下列结论正确的是（）

A、平均数为10，方差为2 B、平均数为11，方差为3 C、平均数为11，方差为2 D、平均数为12，方差为4

查看试题解析
7.
在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S_甲²＞S_乙²；②S_甲²＜S_乙²；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（　　）

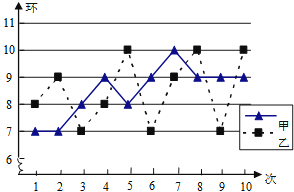A、①③ B、①④ C、②③ D、②④

查看试题解析
8. 已知一组数据的方差为 $\frac{34}{5}$ ，数据为：－1，0，3，5，x，那么x等于（）

A、－2或5.5 B、2或－5.5 C、4或11 D、－4或－11

查看试题解析
9. 根据下表中的信息解决问题：
数据
37
38
39
40
41
频数
8
4
5
a
1
若该组数据的中位数不大于38，则符合条件的正整数a的取值共有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
10. 为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：﹣6，﹣3，x，2，﹣1，3．若这组数据的中位数是﹣1，则下列结论错误的是（　　）

A、方差是8 B、极差是9 C、众数是﹣1 D、平均数是﹣1

查看试题解析

二、填空题

11. 在从小到大排列的五个整数中，中位数是2，唯一的众数是4，则这五个数和的最大值是.

查看试题解析
12. 某学校九（1）班40名同学的期中测试成绩分别为 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ，……， $a_{40}$ .已知 $a_{1}$ + $a_{2}$ + $a_{3}$ +……+ $a_{40}$ = 4800，y= ${(a - a_{1})}^{2}$ + ${(a - a_{2})}^{2}$ + ${(a - a_{2})}^{2}$ +……+ ${(a - a_{40})}^{2}$ ，当y取最小值时，的值为.

查看试题解析
13. 已知：一组自然数1，2，3…k，去掉其中一个数后剩下的数的平均数为16，则去掉的数是．

查看试题解析
14. 已知一组数据4，x，5，y，7，9的平均数为6，众数为5，则这组数据的中位数为.

查看试题解析
15. 一组数据为1，3，5，12，a，其中整数a是这组数据的中位数，则该组数据的平均数是.

查看试题解析
16. 已知数据 $x_{1}$ ， $x_{2}$ ， $\dots$ ， $x_{n}$ 的方差是 $0.1$ ，则 $4 x_{1} - 2$ ， $4 x_{2} - 2$ ， $\dots$ ， $4 x_{n} - 2$ 的方差为.

查看试题解析

三、综合题

17. 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，公司有关部门统计了这15人某月的销售量，如下表所示：

月销售量/件数	1770	480	220	180	120	90
人数	1	1	3	3	3	4

(1)、直接写出这15名营业员该月销售量数据的平均数、中位数、众数；

(2)、如果想让一半左右的营业员都能达到月销售目标，你认为（1）中的平均数、中位数、众数中，哪个最适合作为月销售目标？请说明理由．

温馨提示：确定一个适当的月销售目标是一个关键问题；如果目标定得太高，多数营业员完不成任务，会使营业员失去信心；如果目标定得太低，不能发挥营业员的潜力．

查看试题解析

18. 学校午餐采用自助的形式，并倡导学生和教师“厉行勤俭节约，践行光盘行动” ．学校共有6个年级，且各年级的人数基本相同．为了解午餐的浪费情况，从这6年级中随机抽取了A、B两个年级，进行了连续四周（20个工作日）的调查，得到这两个年级每天午餐浪费饭菜的质量，以下简称“每日餐余质量”（单位：kg），并对这些数据进行了整理、描述和分析．下面给出了部分信息．
a．A年级每日餐余质量的频数分布直方图如下（数据分成6组： $0 \leq x < 2 ， 2 \leq x < 4 ， 4 \leq x < 6 ， 6 \leq x < 8 ， 8 \leq x < 10 ， 10 \leq x < 12)$ ：

b．A年级每日餐余质量在 $6 \leq x < 8$ 这一组的是：6.1，6.6，7.0，7.0，7.0，7.8

c．B年级每日餐余质量如下：1.4，2.8，6.9，7.8，1.9，9.7，3.1，4.6，6.9，10.8，6.9，2.6，7.5，6.9，9.5，7.8，8.4，8.3，9.4，8.8

d．A、B两个年级这20个工作日每日餐余质量的平均数、中位数、众数如下：

年级

平均数

中位数

众数

A

6.4

m

7.0

B

6.6

7.2

n

根据以上信息，回答下列问题：

(1)、m = ， n = ．

(2)、A、B这两个年级中，“厉行勤俭节约，践行光盘行动”做的较好的年级是．

(3)、结合A、B这两个年级每日餐余质量的数据，估计该学校（6个年级）一年（按240个工作日计算）的餐余总质量．

查看试题解析
19. 端午假期刚过，集美龙舟队有开始新的一轮训练，为更加有效训练队员，集美龙舟队决定公开招聘教练，经过笔试后筛选出甲、乙两位教练进行面试和体侧，两人的成绩如右表．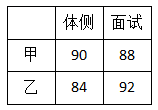

(1)、当体侧成绩权重为6，面试成绩权重为4，请问甲、乙两人谁的成绩高？

(2)、当体侧成绩权重为 $a$ ，面试和体侧各有权重，并且权总和为10，请问当 $a$ 取什么范围，乙成绩比甲高？

查看试题解析
20. 某种水彩笔，在购买时，若同时额外购买笔芯，每个优惠价为3元，使用期间，若备用笔芯不足时需另外购买，每个5元．现要对在购买水彩笔时应同时购买几个笔芯作出选择，为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据．

水笔支数

4

6

8

7

5

需要更换的笔芯个数x

7

8

9

10

11

设x表示水彩笔在使用期内需要更换的笔芯个数，y表示每支水彩笔在购买笔芯上所需要的费用（单位：元），n表示购买水彩笔的同时购买的笔芯个数．

(1)、若x＝9，n＝7，则y＝；若x＝7，n＝9，则y＝；

(2)、若n＝9，用含x的的代数式表示y的取值；

(3)、假设这30支笔在购买时，每支笔同时购买9个笔芯，或每支笔同时购买10个笔芯，分别计算这30支笔在购买笔芯时所需的费用，以费用最省作为选择依据，判断购买一支水彩笔的同时应购买9个还是10个笔芯？

查看试题解析
21. 图1是某市2009年4月5日至14日每天最低气温的折线统计图．

(1)、图2是该市2007年4月5日至14日每天最低气温的频数分布直方图，根据图1提供的信息，补全图2中频数分布直方图；

(2)、在这10天中，最低气温的众数是，中位数是，方差是．

(3)、请用扇形图表示出这十天里温度的分布情况．

查看试题解析

22. 某校为了了解全校400名学生参加课外锻炼的情况，随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查，结果如下：（单位：分）

40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45

(1)、补全频率分布表和频率分布直方图．

分组	频数	频率
4.5﹣22.5	2	0.050
22.5﹣30.5	3
30.5﹣38.5	10	0.250
38.5﹣46.5	19
46.5﹣54.5	5	0.125
54.5﹣62.5	1	0.025
合计	40	1.000

(2)、填空：在这个问题中，总体是，样本是．由统计结果分析的，这组数据的平均数是38.35（分），众数是，中位数是．

(3)、如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况，你认为用平均数、众数、中位数中的哪一个量比较合适？

(4)、估计这所学校有多少名学生，平均每天参加课外锻炼的时间多于30分？

查看试题解析

23. 某县教育局为了对该区八年级数学学科教学质量进行检查，对该区八年级的学生进行摸底，为了解摸底的情况，进行了抽样调查，过程如下，请将有关问题补充完整．

收集数据：随机抽取 $A$ 学校与 $B$ 学校的各20名学生的数学成绩（单位：分）进行分析：

$A$ 学校	91	89	77	86	71	31	97	93	72	91
$A$ 学校	81	92	85	85	95	88	88	90	44	91
$B$ 学校	84	93	66	69	76	87	77	82	85	88
$B$ 学校	90	88	67	88	91	96	68	97	59	88

(1)、整理、描述数据：按如下数据段整理、描述这两组数据

分段

学校

30≤x≤39

40≤x≤49

50≤x≤59

60≤x≤69

70≤x≤79

80≤x≤89

90≤x≤100

$A$ 学校

$B$ 学校

(2)、分析数据：两组数据的平均数、中位数、众数、方差如下表：

统计量

学校

平均数

中位数

众数

方差

$A$ 学校

81.85

268.43

$B$ 学校

81.95

115.25

(3)、得出结论：

$a$ ：若 $A$ 学校有800名八年级学生，估计这次考试成绩80分以上（包含80分）人数为多少人?

$b$ ：根据表格中的数据，推断出哪所学校学生的数学水平较高，并说明理由．（至少从两个不同的角度说明推断的合理性）

查看试题解析

24.

(1)、已知数据99，97，96，98，95，这组数据画成折线图(如图1)。将这组数据的每一个数都减去97，得到一组新数据，在图2中将这组数据画成折线图，则新数据的方差原数据的方差(填“大于”、“等于”、“小于”)。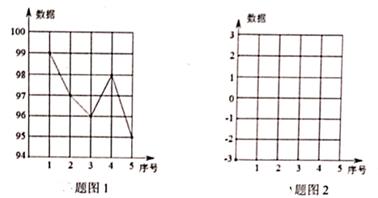

(2)、已知数据5，3，2，4，1，这组数据画成折线图(如图3)。将这组数据的每一个数都乘以2，得到一组新数据，在图4中将这组数据画成折线图，则新数据的方差原数据的方差(填“大于”、“等于”、“小于”)。

(3)、已知甲组数据x₁ ， x₂ ， x₃的平均数为 $\bar{x 甲}$ ，方差为 $S_{甲}^{2}$ 。将这组数据的每一个数都乘以3再加上1，得到乙组数据x₁'=3x₁+1，x₂'=3x₂+1，x₃'=3x₃+1，它们的平均数为 $\bar{x 乙}$ ，方差为 $S_{乙}^{2}$ ，比较 $S_{甲}^{2}$ 与 $S_{乙}^{2}$ 的大小，并说明理由。

查看试题解析

年龄/岁	13	14	15	16
人数	5	15

数据	37	38	39	40	41
频数	8	4	5	a	1

年级	平均数	中位数	众数
A	6.4	m	7.0
B	6.6	7.2	n

水笔支数	4	6	8	7	5
需要更换的笔芯个数x	7	8	9	10	11

初中数学浙教版八年级下册第三章 数据分析初步 章末检测（提高训练）

一、单选题

二、填空题

三、综合题

初中数学浙教版八年级下册第三章数据分析初步章末检测（提高训练）