初中数学浙教版八年级下册第三章数据分析初步章末检测（基础巩固）

试卷更新日期：2021-03-27 类型：单元试卷

进入出卷网下载

一、单选题

1. 某单位要招聘1名英语翻译，张明参加招聘考试的成绩如表所示：若把听、说、读、写的成绩按3：3：2：2计算平均成绩，则张明的平均成绩为（）

听

说

读

写

张明

90

80

83

82

A、82 B、83 C、84 D、85

查看试题解析
2. 数学考试成绩以80分为标准，老师将5位同学的成绩记作：+15，－4，+11，－7，0，则这五名同学的平均成绩为（）

A、3 B、83 C、85 D、84

查看试题解析
3. 一组数据5， 9，7，x，8， 8，5.若这组数据的平均数为7，则这组数据的中位数为（）

A、6 B、7 C、8 D、9

查看试题解析
4. 某校为丰富学生课余活动，开展了一次“校园书法绘画”比赛，共有20名学生入围，他们的决赛成绩如下表：

成绩（分）

94

95

96

97

98

99

人数

1

3

6

5

3

2

则入围学生决赛成绩的中位数和众数分别是（）

A、96分，96分 B、96.5分，96分 C、97分，97分 D、96.5分，97分

查看试题解析
5. 在防治病毒的例行体温检查中，检测到5个人的体温分别是36.8℃、36.4℃、36.5℃、36.9℃、36.4℃，则数据36.8、36.4、36.5、36.9、36.4的众数是（）

A、36.8 B、36.5 C、36.4 D、36.9

查看试题解析
6. 为了解某校计算机考试情况，抽取了50名学生的计算机考试成绩进行统计，统计结果如表所示，则50名学生计算机考试成绩的众数，中位数分别为（）

考试分数（分）

20

16

12

8

人数

24

18

5

3

A、24，18 B、20，16 C、20，12 D、24，5

查看试题解析
7. 测试五位学生的“立定跳远”成绩，得到5个互不相同的数据，在统计时出现一处错误，将最低成绩写得更低了，计算不受影响的是（）

A、方差 B、标准差 C、平均数 D、中位数

查看试题解析
8. 已知一个样本a，4，2，5，3，它的平均数是3，则这个样本的标准差为（）

A、0 B、1 C、 $\sqrt{2}$ D、2

查看试题解析
9. 小明已求出了五个数据：6，4，3，4，□的平均数，在计算它们的方差时，出现了这一步：(3-5)²+(4-5)²+(4-5)²+(6-5)²+（□- 5)*=16(□是后来被遮挡的数据)，则这组数据的众数和方差分别是（）

A、4，5 B、4，3.2 C、6，5 D、4，16

查看试题解析
10. 甲、乙、丙、丁四位同学都参加了5次数学模拟测试，每个人这5次测试的平均成绩都是125分，方差分别是 $S_{甲}^{2} = 0.65 ， S_{乙}^{2} = 0.55 ， S_{丙}^{2} = 0.50 ， S_{丁}^{2} = 0.45$ ，则这五次测试成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

11. 已知一组数据1，7，10，8， $x$ ，6，0，3，若 $\bar{x} = 5$ ，则 $x$ 应等于.

查看试题解析

12. 某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按

50 %

，

20 %

，

30 %

的比例计入学期总评成绩，90分以上为优秀.甲、乙、丙三人的各项成绩如表（单位：分），则学期总评成绩优秀的是.

	纸笔测试	实践能力	成长记录
甲	$90$	$83$	$95$
乙	$88$	$90$	$95$
丙	$90$	$88$	$90$

查看试题解析

13. 已知一组数据－3，x，－2，3，2，6的中位数为2，则其众数是.

查看试题解析
14. 某工厂甲、乙两名工人参加操作技能培训，分别从他们在培训期间参加若干次测试成绩中随机抽取8次，算得两人的平均成绩都是85分，方差分别是S_甲²＝35.5，S_乙²＝41，从操作技能稳定的角度考虑，选派参加比赛

查看试题解析
15. 已知一组数据-3，-2，1，3，6，x的中位数为1，则其方差为．

查看试题解析
16. 甲、乙两台机床生产同一种零件，并且每天产量相等，在6天中每天生产零件中的次品数依次是：甲：3、0、0、2、0、1；乙：1、0、2、1、0、2．则甲、乙两台机床中性能较稳定的是．

查看试题解析

三、解答题

17. 一组数据从小到大顺序排列后为：1，4，6，x，其中位数和平均数相等，求x的值．

查看试题解析
18. 七（1）班共45名学生，在一次数学测试中以90分为标准，超过的记为正，不足的记为负，成绩如下：

人数

5

10

8

12

4

5

1

成绩

-1

+3

-2

+1

+10

0

-4

请你算出这次考试的平均成绩（精确到0.1分）

查看试题解析

19. 某公司招聘职员，对甲、乙两位候选人进行了面试和笔试，面试中包括形体和口才，笔试中包括专业水平和创新能力，他们的成绩（百分制）如下表：

候选人	面试		笔试
候选人	形体	口才	专业水平	创新能力
甲	86	90	96	92
乙	92	86	95	93

(1)、如果公司根据经营性质和岗位要求，以形体、口才、专业水平、创新能力按照5:5:4:6的比确定成绩，请计算甲、乙两人各自的平均成绩，看看谁将被录取？

(2)、如果公司根据经营性质和岗位要求，以面试成绩中形体占5%，口才占30%，笔试成绩中专业水平占35%，创新能力占30%确定成绩，那么你认为该公司应该录取谁？

查看试题解析

20. 某校为了解八年级学生课外阅读情况，随机抽取20名学生平均每周用于课外阅读的时间（单位：min），过程如表；

【收集数据】

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

【整理数据】

课外阅读时间x（min）	0≤x＜40	40≤x＜80	80≤x＜120	120≤x＜160
等级	D	C	B	A
人数	3	a	8	b

【分析数据】

平均数	中位数	众数
80	m	n

请根据以上提供的信息，解答下列问题：

(1)、填空：a＝， b＝， m＝， n＝；

(2)、如果每周用于课外阅读的时间不少于80min为达标，该校八年级现有学生800人，估计八年级达标的学生有多少人？

查看试题解析

21. 某跳水队为了解运动员的年龄情况，作了一次年龄调查，根据跳水运动员的年龄（单位：岁），绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：

(1)、本次接受调查的跳水运动员人数为人，图①中m的值为；

(2)、求统计的这组跳水运动员年龄数据的平均数、众数和中位数．

查看试题解析
22. 甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）：
甲：98，100，100，90，96，91，89，99，100，100，93
乙：98，99，96，94，95，92，92，98，96，99，97

(1)、他们的平均成绩分别是多少？

(2)、甲、乙的11次单元测验成绩的标准差分别是多少？

(3)、这两位同学的成绩各有什么特点？

(4)、现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？

查看试题解析
23. 甲、乙两名射击运动员进行射击比赛，两人在相同条件下各射击10次，射击的成绩如图所示．

根据图中信息，回答下列问题：

(1)、甲的平均数是，乙的中位数是；

(2)、分别计算甲、乙成绩的方差，并从计算结果来分析，你认为哪位运动员的射击成绩更稳定？

查看试题解析

24. 某区举办中学生科普知识竞赛，各学校分别派出一支代表队参赛．知识竞赛满分为100分，规定85分及以上为“合格”，95分及以上为“优秀”。现将A，B两个代表队的竞赛成绩分布图及统计表展示如下：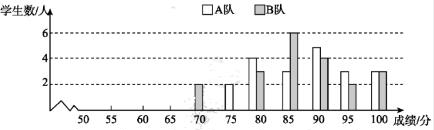

组别	平均分	中位数	方差	合格率	优秀率
A队	88	90	61	70%	30%
B队	a	b	71	75%	25%

(1)、求出成绩统计表中a，b的值。

(2)、小明的成绩虽然在本队排名属中游，但是竞赛成绩低于本队的平均分，那么小明应属于哪个队？

(3)、从平均分、合格率、优秀率、队内成绩的整齐性等方面进行综合评价，你认为集体奖应该颁给哪一队？

查看试题解析