初中数学浙教版九年级下册第三章 投影与三视图 章末检测(提高训练)
试卷更新日期:2021-03-27 类型:单元试卷
一、单选题
-
1. 如图所示,从上面看该几何体的形状图为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
2. 几何体在平面P的正投影,取决于( )
①几何体形状;②投影面与几何体的位置关系;③投影面P的大小
A、①② B、①③ C、②③ D、①②③ -
3. 数学兴趣小组的同学们想利用树影测量树高.课外活动时他们在阳光下测得一根长为1米的竹竿的影子是0.9米,同一时刻测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的台阶上,且影子的末端刚好落在最后一级台阶的上端C处,他们测得落在地面的影长为1.1米,台阶总的高度为1.0米,台阶水平总宽度为1.6米.则树高为( )
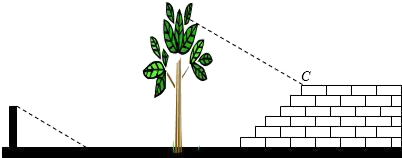 A、3.0m B、4.0m C、5.0m D、6.0m
A、3.0m B、4.0m C、5.0m D、6.0m -
4. 如图,某剧院舞台上的照明灯P射出的光线成“锥体”,其“锥体”面图的“锥角”是60°.已知舞台ABCD是边长为6 m的正方形,要使灯光能照射到整个舞台,则灯P的悬挂高度是( )
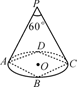 A、 m B、 3 m C、 3 m D、 4 m
A、 m B、 3 m C、 3 m D、 4 m -
5. 如图,大正方体上面正中间放置小正方体,小正方体6个表面写了数字1到6,且所相对面两个数字之和都是7,则这个几何体的左视图为( )
 A、
A、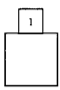 B、
B、 C、
C、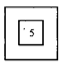 D、
D、
-
6. 如图是一个由多个相同小正方体搭成的几何体的俯视图,图中所标数字为该位置小正方体的个数,则这个几何体的主视图是( )
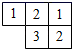 A、
A、 B、
B、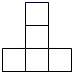 C、
C、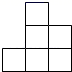 D、
D、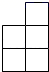
-
7. 有一种正方体如图所示,下列图形是该方体的展开图的是( )
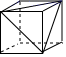 A、
A、 B、
B、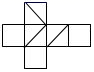 C、
C、 D、
D、
-
8. 《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺3 寸,容纳米2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π=3),则圆柱底周长约为(注:圆柱体的体积=底面积×高)( )
A、1丈3尺 B、5丈4尺 C、9丈2尺 D、48丈6尺 -
9. 已知圆锥的高为 ,母线为 ,且 ,圆锥的侧面展开图为如图所示的扇形.将扇形沿 折叠,使A点恰好落在 上的F点,则弧长 与圆锥的底面周长的比值为( )
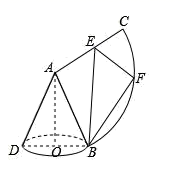 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )
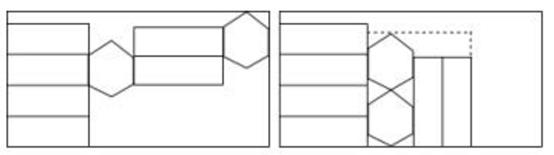 A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2
A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2
二、填空题
-
11. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,点B、B′的坐标分别为(3,1)、(6,2)若点A的坐标为( ,3),则点A′的坐标为 .

-
12. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
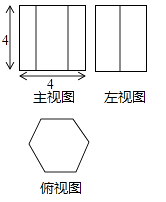
-
13. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.
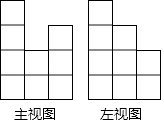
-
14. 如图是一个三级台阶,它的每一级的长、宽、高分别为 , 和 , 和 是这个台阶的两个端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为 .

-
15.
有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2014次后,骰子朝下一面的点数是 .

-
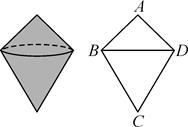
16. 如图物体由两个圆锥组成.其主视图中,∠A=90°,∠ABC=105°.若上面圆锥的侧面积为1,则下面圆锥的侧面积为.
三、解答题
-
17. 一个几何体的三视图如图所示(单位:mm),你能画出这个几何体的图形吗?并求出其表面积和体积.

-
18. 长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少?

-
19. 如图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径是6cm,下底面直径为4cm,母线长为EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积(面积计算结果用
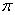 表示) .
表示) . 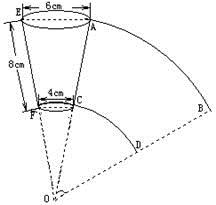
-
20. 如图,是小亮晚上在广场散步的示意图,图中线段 表示站立在广场上的小亮,线段 表示直立在广场上的灯杆,点 表示照明灯的位置.
 (1)、在小亮由 处沿 所在的方向行走到达 处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中画出小亮站在 处的影子 ;(2)、当小亮离开灯杆的距离 时,身高为 的小亮的影长为 ,
(1)、在小亮由 处沿 所在的方向行走到达 处的过程中,他在地面上的影子长度越来越(用“长”或“短”填空);请你在图中画出小亮站在 处的影子 ;(2)、当小亮离开灯杆的距离 时,身高为 的小亮的影长为 ,①灯杆的高度为多少 ?
②当小亮离开灯杆的距离 时,小亮的影长变为多少 ?
-
21. 如图,在一间黑屋子里用一盏白炽灯照一个球.
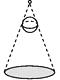 (1)、球在地面上的影子是什么形状?(2)、当把白炽灯向上平移时,影子的大小会怎样变化?(3)、若白炽灯到球心的距离是1 m,到地面的距离是3 m,球的半径是0.2 m,则球在地面上影子的面积是多少?
(1)、球在地面上的影子是什么形状?(2)、当把白炽灯向上平移时,影子的大小会怎样变化?(3)、若白炽灯到球心的距离是1 m,到地面的距离是3 m,球的半径是0.2 m,则球在地面上影子的面积是多少? -
22. 在平整的地面上,有若干个完全相同棱长的小正方体堆成一个几何体,如图所示.
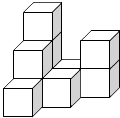 (1)、请画出这个几何体的三视图.(2)、如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色.(3)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
(1)、请画出这个几何体的三视图.(2)、如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色.(3)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
-
23. 如图所示,一透明的敞口正方体容器ABCD﹣A'B'C'D'装有一些液体,棱AB始终在水平桌面上,液面刚好过棱CD , 并与棱BB'交于点Q . 此时液体的形状为直三棱柱,其三视图及尺寸见下图所示请解决下列问题:

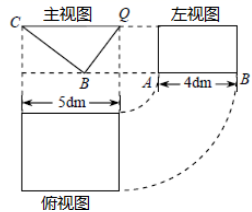 (1)、CQ与BE的位置关系是 , BQ的长是dm:(2)、求液体的体积;(提示:直棱柱体积=底面积×高)(3)、若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°= ,tan37°= )
(1)、CQ与BE的位置关系是 , BQ的长是dm:(2)、求液体的体积;(提示:直棱柱体积=底面积×高)(3)、若容器底部的倾斜角∠CBE=α,求α的度数.(参考数据:sin49°=cos41°= ,tan37°= ) -
24. 如图,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即 ,如T(60°)=1.
 (1)、理解巩固:T(90°)= , T(120°)=;(2)、学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从P点这沿着圆锥的侧面爬行到点Q.
(1)、理解巩固:T(90°)= , T(120°)=;(2)、学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从P点这沿着圆锥的侧面爬行到点Q.①求圆锥侧面展开图的扇形圆心角的数;
②求蚂蚁爬行的最短路径长(精确到0.1).(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
