初中数学浙教版九年级下册第三章 投影与三视图 章末检测(基础巩固)
试卷更新日期:2021-03-27 类型:单元试卷
一、单选题
-
1. 一个等边三角形在太阳光的照射下,在地面上的投影不可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
2. 如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )

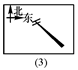
 A、(1)(2)(3)(4) B、(4)(3)(2)(1) C、(4)(3)(1)(2) D、(2)(3)(4)(1)3. 在阳光照射下的升旗广场的旗杆从上午九点到十一点的影子长的变化规律为( )A、逐渐变长 B、逐渐变短 C、影子长度不变 D、影子长短变化无规律4. 一个长方形的正投影不可能是( )A、正方形 B、矩形 C、线段 D、点5. 如图所示的几何体,从正面看到的平面图形是( )
A、(1)(2)(3)(4) B、(4)(3)(2)(1) C、(4)(3)(1)(2) D、(2)(3)(4)(1)3. 在阳光照射下的升旗广场的旗杆从上午九点到十一点的影子长的变化规律为( )A、逐渐变长 B、逐渐变短 C、影子长度不变 D、影子长短变化无规律4. 一个长方形的正投影不可能是( )A、正方形 B、矩形 C、线段 D、点5. 如图所示的几何体,从正面看到的平面图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 如图,水平放置的空心圆柱体的主视图为( )
6. 如图,水平放置的空心圆柱体的主视图为( )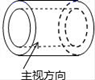 A、
A、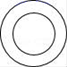 B、
B、 C、
C、 D、
D、 7. 由若干个大小相同的小正方体组成的几何体的三视图如图,则这个几何体只能是( )
7. 由若干个大小相同的小正方体组成的几何体的三视图如图,则这个几何体只能是( )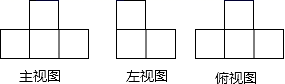 A、
A、 B、
B、 C、
C、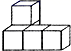 D、
D、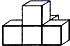 8. 下列图形都是由完全相同的小正方形组成的,将它们分别沿虚线折叠后,不能围成一个小立方体的是( )A、
8. 下列图形都是由完全相同的小正方形组成的,将它们分别沿虚线折叠后,不能围成一个小立方体的是( )A、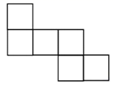 B、
B、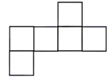 C、
C、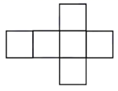 D、
D、 9. 如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC。把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )
9. 如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC。把四边形ABCD绕AB旋转一周,则该几何体的表面积为( ) A、48π B、56π C、68π D、72π10. 用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是( )A、1cm B、2cm C、3cm D、6cm
A、48π B、56π C、68π D、72π10. 用一圆心角为120°,半径为6cm的扇形做成一个圆锥的侧面,则这个圆锥的底面半径是( )A、1cm B、2cm C、3cm D、6cm二、填空题
-
11. 如图,两幅图分别是两棵小树在同一时刻的影子,由此可判断图是在灯光下形成的,图是在太阳光下形成的.
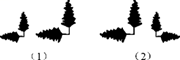 12. 从正面看,从左面看,从上面看都一样的几何体可能是。13. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).
12. 从正面看,从左面看,从上面看都一样的几何体可能是。13. 如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是(结果保留π).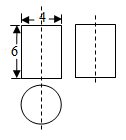 14. 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位: ).则此长方体包装盒的体积是.
14. 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位: ).则此长方体包装盒的体积是. 15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,则该圆锥的母线长l为 .
15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,扇形的圆心角 ,则该圆锥的母线长l为 . 16. 如图是一个正方体的表面展开图,则折成正方体后,与点 重合的点是点.
16. 如图是一个正方体的表面展开图,则折成正方体后,与点 重合的点是点.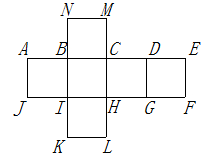
三、解答题
-
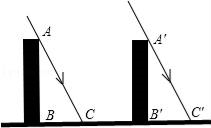
17. 如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.(注:太阳光线可看成是平行的)
 18. 观察:下图中的几何体是由若干个完全相同的小正方体搭成的.
18. 观察:下图中的几何体是由若干个完全相同的小正方体搭成的.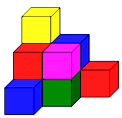
(1)、画出几何体的主视图,左视图,俯视图;(2)、能移走一个小正方体使它的三个视图都不变吗?
19. 如图是由几个小立方块搭成的几何体从上面看到的图形,小正方形的数字表示该位置小立方块的个数,请在左面的方格表中分别画出从正面和左面看到的图形. 20. 两棵树(大树和小树)在一盏路灯下的影子如图所示
20. 两棵树(大树和小树)在一盏路灯下的影子如图所示 (1)、确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).(2)、若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.21.(1)、如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
(1)、确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).(2)、若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.21.(1)、如图①是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图名称;
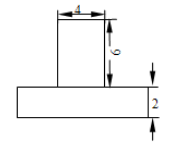 视图
视图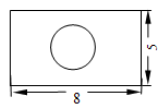 视图(2)、根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)22. 如图,圆锥底面的半径为10cm,高为10 cm.
视图(2)、根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)22. 如图,圆锥底面的半径为10cm,高为10 cm.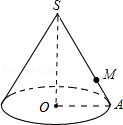 (1)、求圆锥的全面积;(2)、若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.
(1)、求圆锥的全面积;(2)、若一只蚂蚁从底面上一点A出发绕圆锥一周回到SA上一点M处,且SM=3AM,求它所走的最短距离.