初中数学浙教版九年级下册3.4.1几何体的展开图 同步练习
试卷更新日期:2021-03-27 类型:同步测试
一、单选题
-
1. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
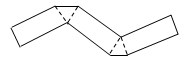 A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥2. 下列是正方体展开图的是( )A、
A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥2. 下列是正方体展开图的是( )A、 B、
B、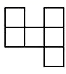 C、
C、 D、
D、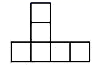 3. 如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的序号是( )
3. 如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的序号是( )
圆柱 正方体 三棱柱 四棱锥
A、 B、 C、 D、4. 下列几何体的侧面展开图形状不是矩形的是( )A、圆柱 B、圆锥 C、正方体 D、棱柱5. 一个几何体的表面展开图如图所示,则这个几何体是( )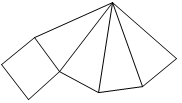 A、圆锥 B、三棱锥 C、四棱柱 D、四棱锥6. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A、圆锥 B、三棱锥 C、四棱柱 D、四棱锥6. 下面四个图形中,经过折叠能围成如图所示的几何图形的是( )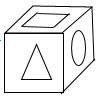 A、
A、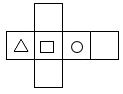 B、
B、 C、
C、 D、
D、 7. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字一面的相对面上的字是( )
7. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字一面的相对面上的字是( )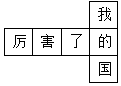 A、厉 B、害 C、了 D、国8. 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A , B在围成的正方体上的距离是( )
A、厉 B、害 C、了 D、国8. 如图1是边长为1的六个小正方形组成的平面图形,将它围成图2的正方体,则图1中小正方形顶点A , B在围成的正方体上的距离是( ) A、 B、 C、1 D、09. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .
A、 B、 C、1 D、09. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .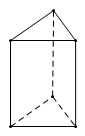 A、28 B、31 C、34 D、3610. 如图,长方体的底面邻边长分别是5cm和7cm,高为20cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B(点B为棱的中点),那么所用细线最短为( )
A、28 B、31 C、34 D、3610. 如图,长方体的底面邻边长分别是5cm和7cm,高为20cm,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B(点B为棱的中点),那么所用细线最短为( ) A、20cm B、24cm C、26cm D、28cm
A、20cm B、24cm C、26cm D、28cm二、填空题
-
11. 第一行的平面图形经过折叠后能对应得到第二行的几何体,请你在横线上把它们的序号对应写出来 .
 12. 如图是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,且相对面上的两个数互为相反数,那么代数式 的值等于.
12. 如图是一个正方体的表面展开图,已知正方体的每一个面都有一个有理数,且相对面上的两个数互为相反数,那么代数式 的值等于. 13. 长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .14. 一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为cm3.
13. 长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .14. 一个无盖的长方形包装盒展开后如图所示(单位:cm),则其容积为cm3.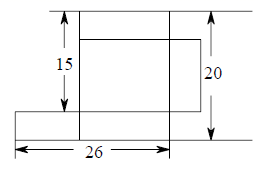
三、解答题
-
15. 在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30cm、宽20cm、高18cm,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
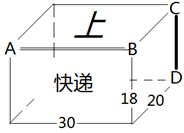
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
16. 如图,李明用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,王华看来看去总觉得所拼图形似乎存在问题. (1)、请你帮李明分析一下拼图是否存在问题.若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(1)、请你帮李明分析一下拼图是否存在问题.若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全.
(2)、若图中的正方形边长为2 cm,长方形的长为3 cm,宽为2 cm,请直接写出修正后所折叠而成的长方体的容积为多少cm3 .17. 小明用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小明看来看去觉得所拼图形似乎存在问题. (1)、请你帮小明分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;(2)、若图中的正方形边长6cm,长方形的长为8cm,宽为6cm,请求出修正后所折叠而成的长方体的表面积和体积.18. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)、请你帮小明分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;(2)、若图中的正方形边长6cm,长方形的长为8cm,宽为6cm,请求出修正后所折叠而成的长方体的表面积和体积.18. 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: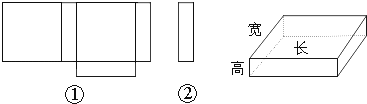 (1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
(1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.(3)、小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.