甘肃省2020-2021学年高三理数第一次高考诊断试卷

试卷更新日期：2021-03-25 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x - 3 < 0}$ ， $B = {- 1, 1, 2}$ ，则 $A \cap B =$ （）

A、 ${1, 2}$ B、 ${- 1, 1, 2}$ C、 ${0, 1, 2}$ D、 ${- 1, 0, 12, 3}$

查看试题解析
2. 若复数 $z$ 满足 $(1 + 2 i) z = | \frac{1}{2} + \frac{\sqrt{3}}{2} i |$ ，则 $z$ 的共轭复数是（）

A、 $- \frac{1}{5} + \frac{2}{5} i$ B、 $- \frac{1}{5} - \frac{2}{5} i$ C、 $\frac{1}{5} + \frac{2}{5} i$ D、 $\frac{1}{5} - \frac{2}{5} i$

查看试题解析
3. 抛物线 $y^{2} = - 2 p x (p > 0)$ 的准线经过椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ 的右焦点，则 $p =$ （）

A、2 B、4 C、8 D、12

查看试题解析
4. 甲、乙两名射击运动爱好者在相同条件下各射击10次，中靶环数情况如图所示．则甲、乙两人中靶环数的方差分别为（）

A、7，7 B、7，1.2 C、1.1，2.3 D、1.2，5.4

查看试题解析
5. 已知函数 $f (x) = x (e^{x} - e^{- x})$ ，则 $f (x)$ （）

A、是奇函数，且在 $(0 ， + \infty)$ 单调递减 B、是奇函数，且在 $(0 ， + \infty)$ 单调递增 C、是偶函数，且在 $(0 ， + \infty)$ 单调递减 D、是偶函数，且在 $(0 ， + \infty)$ 单调递增

查看试题解析
6. 已知 $m$ ， $n$ 表示两条不同直线， $α$ ， $β$ 表示两个不同平面．设有四个命题： $p_{1}$ ：若 $m // α$ ， $m ⊥ n$ ，则 $n ⊥ α$ ； $p_{2}$ ：若 $m // α$ ， $n ⊥ α$ ，则 $m ⊥ n$ ； $p_{3}$ ：若 $m // α$ ， $α ⊥ β$ ，则 $m // β$ ； $p_{4}$ ：若 $m // α$ ， $m // β$ ，则 $α // β$ ．则下列复合命题中为真命题的是（）

A、 $p_{1} \land p_{2}$ B、 $\neg p_{1} \land p_{4}$ C、 $p_{2} \lor p_{3}$ D、 $p_{3} \lor p_{4}$

查看试题解析
7. 由伦敦著名建筑事务所Steyn Studio设计的南非双曲线大教堂惊艳世界，该建筑是数学与建筑完美结合造就的艺术品．若将如图所示的大教堂外形弧线的一段近似看成双曲线 $\frac{y^{2}}{a^{2}} - \frac{x^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 下支的一部分，且此双曲线的下焦点到渐近线的距离为2，离心率为2，则该双曲线的渐近线方程为（）

A、 $y = \pm \sqrt{3} x$ B、 $y = \pm \frac{\sqrt{3}}{3} x$ C、 $y = \pm x$ D、 $y = \pm 2 x$

查看试题解析
8. 已知 $α$ 是第四象限角，且 $\sin α = - \frac{\sqrt{5}}{5}$ ，则 $\cos (2 α + \frac{π}{4}) =$ （）

A、 $- \frac{\sqrt{2}}{10}$ B、 $\frac{\sqrt{2}}{10}$ C、 $- \frac{7 \sqrt{2}}{10}$ D、 $\frac{7 \sqrt{2}}{10}$

查看试题解析
9. 圆 $x^{2} + y^{2} = 4$ 上任意一点 $M$ 到直线 $3 x + 4 y - 15 = 0$ 的距离大于 $2$ 的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{5}{6}$

查看试题解析
10. 玉琮是一种内圆外方的筒型玉器，它与玉璧、玉圭、玉璋、玉璜、玉琥被称为“六器”，是古人用于祭祀神祇的一种礼器．《周礼》中载有“以玉作六器，以礼天地四方，以苍璧礼天，以黄琮礼地”等文．如图为齐家文化玉琮，该玉琮中方内空，形状对称，圆筒内径 $2.0 cm$ ，外径 $2.4 cm$ ，筒高 $6.0 cm$ ，方高 $4.0 cm$ ，则其体积约为（单位： ${cm}^{3}$ ）（）

A、 $23.04 - 3.92 π$ B、 $34.56 - 3.92 π$ C、 $34.56 - 3.12 π$ D、 $23.04 - 3.12 π$

查看试题解析
11. 在 $△ A B C$ 中， $A = 120 °$ ， $B C = 6$ ，则 $△ A B C$ 的面积的最大值为（）

A、 $\frac{1}{2}$ B、1 C、 $\frac{3 \sqrt{3}}{2}$ D、 $3 \sqrt{3}$

查看试题解析
12. 设实数 $λ > 0$ ，若对任意的 $x \in (1 ， + \infty)$ ，不等式 $e^{λ x} - \frac{\ln x}{λ} ⩾ 0$ 恒成立，则 $λ$ 的最小值为（）

A、 $\frac{1}{e}$ B、 $\frac{1}{2 e}$ C、 $\frac{2}{e}$ D、 $\frac{e}{3}$

查看试题解析

二、填空题

13. 设 $a = \log_{2021}^{\sqrt{2022}}$ ， $b = 2021^{\frac{1}{2022}}$ ， $c = \log_{2022} \frac{1}{2021}$ ，则 $a$ ， $b$ ， $c$ 的大小关系是．（按照从大到小的顺序排列）

查看试题解析
14. 已知向量 $\vec{a}$ 与向量 $\vec{b}$ 夹角为 $60 °$ ，且 $| \vec{a} | = 1$ ， $\vec{b} = (3, 4)$ ，要使 $2 \vec{a} + λ \vec{b}$ 与 $\vec{a}$ 垂直，则 $λ =$ ．

查看试题解析
15. ${(1 - 2 x)}^{5} {(1 + x)}^{4}$ 展开式中 $x^{3}$ 的系数为．

查看试题解析
16. 函数 $f (x) = \cos 2 x - \sqrt{3} \sin 2 x$ ， $x \in R$ ，有下列命题：
① $y = f (x)$ 的表达式可改写为 $y = 2 \cos (2 x + \frac{π}{3})$ ；

②直线 $x = \frac{π}{12}$ 是函数 $f (x)$ 图象的一条对称轴；

③函数 $f (x)$ 的图象可以由函数 $y = 2 \sin 2 x$ 的图象向右平移 $\frac{π}{6}$ 个单位长度得到；

④满足 $f (x) \leq \sqrt{3}$ 的 $x$ 的取值范围是 ${x | - \frac{π}{12} + k π \leq x \leq \frac{3 π}{4} + k π ， k \in Z}$ ．

其中正确的命题序号是．（注：把你认为正确的命题序号都填上）

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{1} = 1$ ， $S_{n} = \frac{1}{2} a_{n + 1} (n \in N^{*})$ ．

(1)、求 $S_{n}$ ；

(2)、设 $b_{n} = \log_{\sqrt{3}} S_{n}$ ，求使得 $\frac{1}{b_{2} b_{3}} + \frac{1}{b_{3} b_{4}} + \cdot \cdot \cdot + \frac{1}{b_{n + 1} b_{n + 2}} > \frac{99}{400}$ 成立的最小正整数 $n$ ．

查看试题解析

18. 2020年10月，中共中央办公厅、国务院办公厅印发了《关于全面加强和改进新时代学校体育工作的意见》，某地积极开展中小学健康促进行动，发挥以体育智、以体育心功能，决定在2021年体育中考中再增加一定的分数，规定：考生须参加立定跳远、掷实心球、一分钟跳绳三项测试，其中一分钟跳绳满分20分．学校为掌握九年级学生一分钟跳绳情况，随机抽取了100名学生测试，其成绩均在

[165 ， 215]

间，并得到如图所示频率分布直方图，计分规则如下表：

一分钟跳绳个数	$[165 ， 175)$	$[175 ， 185)$	$[185 ， 195)$	$[195 ， 205)$	$[205 ， 215]$
得分	16	17	18	19	20

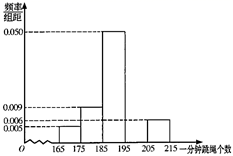(1)、补全频率分布直方图，并根据频率分布直方图估计样本中位数；

(2)、若两人可组成一个小队，并且两人得分之和小于35分，则称该小队为“潜力队”，用频率估计概率，求从进行测试的100名学生中任意选取2人，恰好选到“潜力队”的概率．

查看试题解析

19. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为梯形， $P A = P D = 2 \sqrt{2}$ ， $D C = A D = 2 A B = 4$ ， $A B ⊥ A D$ ， $A B // C D$ ，平面 $P A D ⊥$ 平面 $A B C D$ ， $E$ 为棱 $P B$ 上一点．

(1)、在平面 $P A B$ 内能否作一条直线与平面 $P A D$ 垂直？若能，请画出直线并加以证明；若不能，请说明理由；

(2)、若 $\frac{P E}{P B} = \frac{1}{3}$ 时，求直线 $A E$ 与平面 $P B C$ 所成角的正弦值．

查看试题解析
20. 已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦距为 $4$ ，且经过点 $P (2, 3)$ ．

(1)、求椭圆 $C$ 的方程；

(2)、设椭圆 $C$ 上存在两点 $M$ ， $N$ ，使得 $P M$ 的斜率与 $P N$ 的斜率之和为-1，直线 $M N$ 是否过定点？若是，求出定点的坐标；若不是，说明理由．

查看试题解析
21. 已知函数 $f (x) = \frac{1}{2} x^{2} - (a + 1) x + a \ln x$ ．

(1)、求函数 $f (x)$ 的单调区间；

(2)、设函数 $g (x) = 2 f (x) - (2 a + x) \ln x + 2 x - 4 a + 2$ ，若 $g (x)$ 在 $[\frac{1}{2} ， + \infty)$ 上有两个零点，求实数 $a$ 的取值范围．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知点 $P$ 的坐标为 $(0, 2)$ ，直线 $C_{1}$ 的方程为： ${\begin{array}{l} x = t \cos α \\ y = 2 + t \sin α \end{array}$ （其中 $t$ 为参数）．以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，曲线 $C_{2}$ 的极坐标方程为： $ρ \cos^{2} θ + 4 \sqrt{3} \cos θ - ρ = 0$ ．

(1)、将直线 $C_{1}$ 的方程化为普通方程，曲线 $C_{2}$ 的方程化为直角坐标方程；

(2)、若直线 $C_{1}$ 过点 $Q (\sqrt{3}, - 1)$ 且交曲线 $C_{2}$ 于 $A$ ， $B$ 两点，设线段 $A B$ 的中点为 $M$ ，求 $| P M |$ ．

查看试题解析
23. 已知函数 $f (x) = | 2 x + a |$ ， $g (x) = | x - b |$ ．

(1)、若 $a = 1$ ， $b = 3$ ，解不等式 $f (x) + g (x) \geq 4$ ；

(2)、当 $a > 0$ ， $b > 0$ 时， $f (x) - 2 g (x)$ 的最大值是 $3$ ，证明： $a^{2} + 4 b^{2} \geq \frac{9}{2}$ ．

查看试题解析