山西省临汾市尧都区2020年中考数学四模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（　　）

A、 $\frac{1}{4}$ B、π C、 $\sqrt{9}$ D、﹣ $\frac{23}{7}$

查看试题解析
2. 如图，直线 $a // b$ ， $∠ 1 = 80 °$ ， $∠ 3 = 120 °$ ，则 $∠ 2$ 的度数为(　　)

A、40° B、50° C、60° D、70°

查看试题解析
3. 为了解某校学生今年五一期间参加社团活动时间的情况，随机抽查了其中100名学生进行统计，并绘制成如图所示的频数直方图，已知该校共有1000名学生，据此估计，该校五一期间参加社团活动时间在8～10小时之间的学生数大约是（）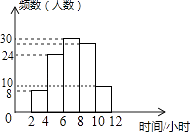

A、280 B、240 C、300 D、260

查看试题解析
4. 据2019年2月山西统计信息报道，2018年山西省粮食总产量达到13800000000 kg ，比上年增长1.9%．数据13800000000用科学记数法表示为(　　)

A、 $138 \times 10^{8}$ B、 $1.38 \times 10^{8}$ C、 $1.38 \times 10^{9}$ D、 $1.38 \times 10^{10}$

查看试题解析
5. 一元二次方程 $y^{2} - y - \frac{3}{4} = 0$ 配方后可化为（）

A、 ${(y + \frac{1}{2})}^{2} = 1$ B、 ${(y - \frac{1}{2})}^{2} = 1$ C、 ${(y + \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(y - \frac{1}{2})}^{2} = \frac{3}{4}$

查看试题解析
6. 如图所示， $▱ A B C D$ 中，E为BC边上一点，以AE为边作正方形AEFG ，若 $∠ B A E = 40 °$ ， $∠ C E F = 15 °$ ，则 $∠ C$ 的度数是(　　)

A、115° B、105° C、75° D、65°

查看试题解析
7. 如图，已知△ABC的三个顶点均在正方形格点上，则 $\cos A$ 的值为(　　)

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{5}}{5}$ C、 $\frac{2 \sqrt{3}}{3}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
8. 如图，直线 $y = k x + b$ ( $k \neq 0$ )经过点A(－2，4)，则不等式 $k x + b < 4$ 的解集为(　　)

A、 $x > - 2$ B、 $x < - 2$ C、 $x > 4$ D、 $x < 4$

查看试题解析
9. 如图，在平面直角坐标系中，△ABC的顶点都在正方形网格线的格点上，将△ABC绕点P按逆时针方向旋转90°，得到 $△ A^{'} B^{'} C^{'}$ ，则点P的坐标为(　　)

A、(0，0) B、(0，1) C、(－1，1) D、(1，1)

查看试题解析
10. 如图，过x轴正半轴上的任意一点P ，作y轴的平行线，分别与反比例函数 $y = - \frac{5}{x} (x > 0)$ 和 $y = \frac{3}{x} (x > 0)$ 的图象交于A ， B两点．若点C是y轴上任意一点，点D是AP的中点，连接DC ， BC ，则△DBC的面积为(　　)

A、 $\frac{9}{4}$ B、4 C、5 D、 $\frac{11}{4}$

查看试题解析

二、填空题

11. 用形状和大小相同的按如图所示的方式排列，按照这样的规律，第 $n$ 个图形有个．

查看试题解析
12. 我国元朝数学家朱世杰的数学著作《四元玉鉴》中有一个“二果问价”问题：九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个？又问各该几个钱？若设买甜果、苦果的个数分别是 $x$ 个和 $y$ 个，根据题意，可列方程组为.

查看试题解析
13. 体育课上，各小组同学进行踢毽子比赛活动，第一小组五名同学单位时间踢毽子的个数分别为103，102，98，100，97．这组数据的方差是．

查看试题解析
14. 如图，无人机A的高度为270 m ，从A处看一栋大楼顶部B的俯角为30°，看底部C的俯角为60°，则这栋大楼的高度为m．

查看试题解析
15. 如图，在△ABC中，AB=10，AC=8，∠BAC=45°，AD是∠BAC的平分线， DE⊥AB于点E，则DE的长是

查看试题解析

三、解答题

16.

(1)、计算： ${(\frac{1}{2})}^{- 2} - 2^{3} \times 0.125 + 3^{0} + | 1 - \sqrt{2} |$ ；

(2)、先化简，再求值： $\frac{3 x - 3}{x^{2} - 1} \div \frac{3 x}{x^{2} + 2 x + 1} + \frac{1}{x^{2} - x}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
17. 已知△ABC在平面直角坐标系内，三个顶点的坐标分别为A(0，3)，B(4，5)，C(3，2)．(正方形网格中，每个小正方形的边长都是1个单位长度)

⑴画出△ABC向下平移5个单位长度得到的 $△ A_{1} B_{1} C_{1}$ ，并直接写出点 $C_{1}$ 的坐标；

⑵以点B为位似中心，在网格中画出 $△ A_{2} B C_{2}$ ，使 $△ A_{2} B C_{2}$ 与 $△ A B C$ 位似，且相似比为2∶1，并直接写出 $△ A_{2} B C_{2}$ 的面积．

查看试题解析
18. 阅读下面内容，并解决问题：
《名画》中的数学

前苏联著名科学家别莱利曼在他所著的《趣味代数学》中介绍了波格达诺夫·别列斯基的《名画》，画上那位老师拉金斯基是一位自然科学教授，放弃了大学教席(教师职务)来到农村学校当一名普通老师．画中，黑板上写着一道式子，如图所示：

从这道算式计算可以得出答案等于2，如果仔细一研究，10，11，12，13，14这几个数具有一种有趣的特性： $10^{2} + 11^{2} + 12^{2} = 13^{2} + 14^{2}$ ，而且 $100 + 121 + 144 = 365$ ．

请解答以下问题：

(1)、还有没有其他像这样五个连续的整数，前三个数的平方和正好等于后两个数的平方和呢？如果有，请求出另外的五个连续的整数；

(2)、若七个连续整数前四个数的平方和等于后三个数的平方和，请直接写出符合条件的连续整数．

查看试题解析
19. 酒令是中国民间风俗之一．白居易曾诗曰：“花时同醉破春愁，醉折花枝当酒筹”饮酒行令，是中国人在饮酒时助兴的一种特有方式，不仅要以酒助兴，往往还伴之以赋诗填词、猜迷形拳之举，最早诞生于西周，完备于隋唐，“虎棒鸡虫令”是其中一种：“二人相对，以筷子相声，同时或喊虎、喊棒、喊鸡、喊虫，以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负，负者饮．若棒兴鸡、或虫兴虎同时出现（解释：若棒与鸡，虎与虫同时喊出）或两人喊出同一物，则不分胜负，继续喊”．依据上述规则，张三和李四同时随机地喊出其中一物，两人只喊一次．

(1)、求张三喊出“虎”取胜的概率；

(2)、用列表法或画树状图法，求李四取胜的概率；

(3)、直接写出两人能分出胜负的概率．

查看试题解析
20. 如图△ABC内接于⊙O ， $∠ A C B = 60 °$ ，BD是⊙O的直径，点P是BD延长线上一点，且PA是⊙O的切线．

(1)、求证： $A P = A B$ ；

(2)、若 $P D = \sqrt{5}$ ，求⊙O的直径．

查看试题解析
21. 某网店准备销售一种多功能旅行背包，计划从厂家以每个120元的价格进货.

(1)、经过市场调查发现，当每个背包的售价为140元时，月均销量为980个，售价每增长10元，月均销量就相应减少30个，若使这种背包的月均销量不低于800个，每个背包售价应不高于多少元？

(2)、在实际销售过程中，由于原材料涨价和生产成本增加的原因，每个背包的进价为150元，而每个背包的售价比（1）中最高售价减少了a%（a＞0），月均销量比（1）中最低月均销量800个增加了5a%，结果该店销售该背包的月均利润达到了40000元，求在实际销售过程中每个背包售价为多少元？

查看试题解析
22. 综合与实践
问题情境：

小明将两个全等的 $Rt △ A B C$ 和 $R t △ D E F$ 重叠在一起，其中 $∠ A C B = ∠ D F E = 90 °$ ， $∠ A B C = ∠ D E F = 30 °$ ， $A C = 1$ . 固定△DEF不动，将△ABC沿直线ED向左平移，当B与D重合时停止移动．

(1)、猜想证明：
如图1，在平移过程中，当点D为AB中点时，连接DC ， CF ， BF ，请你猜想四边形CDBF的形状，并证明你的结论；

(2)、如图2，在平移过程中，连接DC ， CF ， FB ，四边形CDBF的形状在不断地变化，判断它的面积变化情况，并求出其面积；
探索发现：

(3)、在平移过程中，四边形CDBF有什么共同特征？(写出两个即可) ，；

(4)、请你提出一个与△ABC平移过程有关的新的数学问题(不必证明和解答)．

查看试题解析
23. 综合与探究
如图，抛物线 $y = \frac{1}{4} x^{2} - \frac{1}{2} x - 2$ ，与x轴交于A ， B两点(点A在点B的左侧)，与y轴交于点C ，抛物线的对称轴为l ．

(1)、求点A ， B ， C的坐标；

(2)、若点D是第一象限内抛物线上一点，过点D作 $D E ⊥ x$ 轴于点E ，交直线BC于点F ，当 $O E = 4 D F$ 时，求四边形DOBF的面积；

(3)、在（2）的条件下，若点M在抛物线上，点N在抛物线的对称轴上，是否存在以点B ， D ， M ， N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

查看试题解析