内蒙古包头市35中2020年中考数学三模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 的相反数为A、 B、3 C、 D、2. 下列计算正确的是 ( )A、 B、 C、 D、3. 已知某几何体的三视图如图所示,则该几何体可能是( )
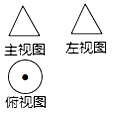 A、
A、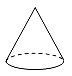 B、
B、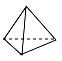 C、
C、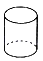 D、
D、 4. 如图, 的顶点都是正方形网格中的格点,则 等于( )
4. 如图, 的顶点都是正方形网格中的格点,则 等于( )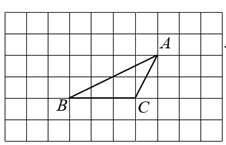 A、 B、 C、 D、5. 某校一九年级毕业班为了了解学生100米跑的训练情况,对全班学生进行了一次测试,测试结果如条形统计图所示,则测试成绩的中位数和众数分别是( )
A、 B、 C、 D、5. 某校一九年级毕业班为了了解学生100米跑的训练情况,对全班学生进行了一次测试,测试结果如条形统计图所示,则测试成绩的中位数和众数分别是( )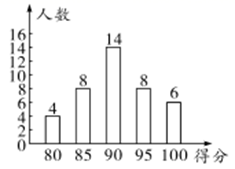 A、85分,90分 B、90分,90分 C、90分,95分 D、95分,95分6. 如图,在 的两边上分别截取OA、OB,使 ;分别以点 为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC若 ,四边形 的面积为 .则OC的长为( )
A、85分,90分 B、90分,90分 C、90分,95分 D、95分,95分6. 如图,在 的两边上分别截取OA、OB,使 ;分别以点 为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC若 ,四边形 的面积为 .则OC的长为( )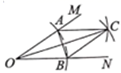 A、 B、 C、 D、7. 等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是 ( )A、8 B、9 C、8或9 D、128. 若 则( )A、 B、 C、 D、9. 设点 和点 是反比例函数 图象上的两点,当 时, ,则一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,已知AB是ʘO的直径,点P在B的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C.若⊙O的半径为6.BC=9,则PA的长为( )
A、 B、 C、 D、7. 等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是 ( )A、8 B、9 C、8或9 D、128. 若 则( )A、 B、 C、 D、9. 设点 和点 是反比例函数 图象上的两点,当 时, ,则一次函数 的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 如图,已知AB是ʘO的直径,点P在B的延长线上,PD与⊙O相切于点D,过点B作PD的垂线交PD的延长线于点C.若⊙O的半径为6.BC=9,则PA的长为( )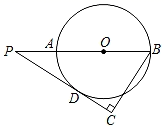 A、8 B、4 C、6 D、511. 下列命题中,假命题的是( )A、若 ,则 B、若 ,则 C、如果两个三角形相似,则他们的面积比等于相似比的平方 D、有一个角相等的两个菱形相似12. 如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x , 0)且﹣2<x<3,BC⊥AC垂足为点C , 连接AB . 若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
A、8 B、4 C、6 D、511. 下列命题中,假命题的是( )A、若 ,则 B、若 ,则 C、如果两个三角形相似,则他们的面积比等于相似比的平方 D、有一个角相等的两个菱形相似12. 如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x , 0)且﹣2<x<3,BC⊥AC垂足为点C , 连接AB . 若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )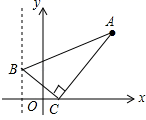 A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
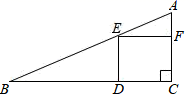
13. 在函数y= +(x﹣3)0中自变量x的取值范围是 .14. 如果 ,那么代数式 的值是 .15. 现有三张分别标有数字1、2、3的卡片,它们除了数字外完全相同,把卡片背面朝上洗匀,从中任意抽取一张,将上面的数字记为a;将卡片放回后,再次任意抽取一张,将上面的数字记为b , 则点 在直线 图象上的概率为 .16. 如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF , 点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为
 17. 如图,△ABC中,D,E两点分别在边AB,BC上,若AD:DB=CE:EB=3:4,记△DBE的面积为S1 , △ADC的面积为S2 , 则S1:S2= 。
17. 如图,△ABC中,D,E两点分别在边AB,BC上,若AD:DB=CE:EB=3:4,记△DBE的面积为S1 , △ADC的面积为S2 , 则S1:S2= 。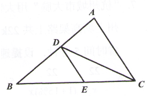 18. 如图,平面直角坐标系 中,点B是 的图象上一点,点A是直线 上的一动点,且 .当 的面积等于5时,k的值为 .
18. 如图,平面直角坐标系 中,点B是 的图象上一点,点A是直线 上的一动点,且 .当 的面积等于5时,k的值为 .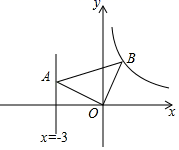 19. 如图,AD 是△ABC 的角平分线,DE , DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE . 其中正确的是(填序号).
19. 如图,AD 是△ABC 的角平分线,DE , DF 分别是△BAD 和△ACD 的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形 AEDF 是正方形;④AE+DF=AF+DE . 其中正确的是(填序号).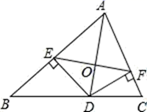 20. 如图,在平面直角坐标系中,点A坐标为 ,过A点作y轴垂线,点B , C在该垂线上,B点坐标为 ,C点在B点右侧,且 ,则C点的坐标为 .
20. 如图,在平面直角坐标系中,点A坐标为 ,过A点作y轴垂线,点B , C在该垂线上,B点坐标为 ,C点在B点右侧,且 ,则C点的坐标为 .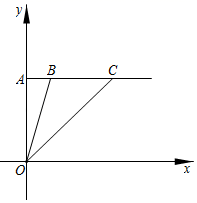
三、解答题
-
21. 某校对九年级学生进行一次综合文科中考模拟测试,成绩x分(x为整数)评定为优秀、良好、合格、不合格四个等级(优秀、良好、合格、不合格分别用A、B、C、D表示),A等级:90≤x≤100,B等级:80≤x<90,C等级:60≤x<80,D等级:0≤x<60.该校随机抽取了一部分学生的成绩进行调查,并绘制成如图不完整的统计图表.
等级
频数(人数)
频率
A
a
20%
B
16
40%
C
b
m
D
4
10%
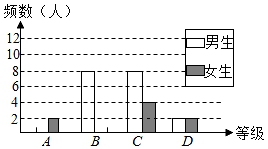
请你根据统计图表提供的信息解答下列问题:
(1)、上表中的a , b= , m=.(2)、本次调查共抽取了多少名学生?请补全条形图.(3)、若从D等级的4名学生中抽取两名学生进行问卷调查,请用画树状图或列表的方法求抽取的两名学生恰好是一男一女的概率.22. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.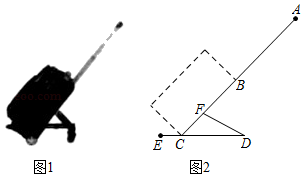 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).23. 某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.(1)、求:甲、乙玩具的进货单价各是多少元?(2)、玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?24. 已知:如图所示,MN是 的直径,B是 上一点,NP平分 交 于P,过P作 于A.
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).23. 某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的 ,已知甲玩具的进货单价比乙玩具的进货单价多1元.(1)、求:甲、乙玩具的进货单价各是多少元?(2)、玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?24. 已知:如图所示,MN是 的直径,B是 上一点,NP平分 交 于P,过P作 于A.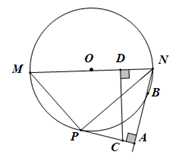 (1)、求证:PA与 相切;(2)、若 , ,求MP的长;(3)、若D是ON中点,过D作 交AP于C,若 , ,求 的半径.25. 已知:在 中 ,点D为 边的中点,点F是 边上一点,点E在线段 的延长线上, ,点M在线段 上, .
(1)、求证:PA与 相切;(2)、若 , ,求MP的长;(3)、若D是ON中点,过D作 交AP于C,若 , ,求 的半径.25. 已知:在 中 ,点D为 边的中点,点F是 边上一点,点E在线段 的延长线上, ,点M在线段 上, .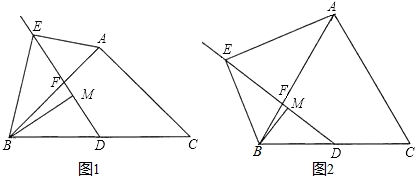 (1)、如图1,当 时,求证: ;(2)、如图2,当 时,则线段 、 之间的数量关系为:.(3)、在(2)的条件下延长 到P , 使 ,连接 ,若 ,求 值.26. 如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)、如图1,当 时,求证: ;(2)、如图2,当 时,则线段 、 之间的数量关系为:.(3)、在(2)的条件下延长 到P , 使 ,连接 ,若 ,求 值.26. 如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).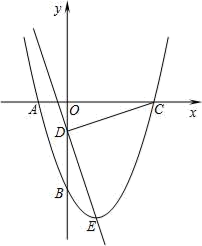 (1)、求抛物线的函数解析式;(2)、点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)、在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
(1)、求抛物线的函数解析式;(2)、点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;(3)、在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.