云南省2020年中考数学一模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、填空题

1. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是今有两数若其意义相反，则分别叫做正数与负数．若气温零上 $5 ℃$ 记做 $+ 5 ℃$ ，若气温零下 $3 ℃$ ，则记作 $℃$ ．

查看试题解析
2. 如图，若 $A B / / C D$ ，点E在直线 $A B$ 的上方，连接 $A E ， C E$ ，延长 $E A$ 交 $C D$ 于点F，已知 $∠ D C E = 99 °$ ， $∠ C E F = 35 °$ ，则 $∠ E A B =$ °．

查看试题解析
3. 要使 $\frac{10}{2 x - 3}$ 有意义，则x的取值范围是．

查看试题解析
4. 如图，在一边长为 $2cm$ 的正六边形 $A B C D E F$ 中，分别以点A，D为圆心， $A B ， D C$ 长为半径，作扇形 $A B F$ ，扇形 $D C E$ ，则图中阴影部分的面积为 ${cm}^{2}$ ．（结果保留 $π$ ）

查看试题解析
5. 若关于x的一元二次方程 $x^{2} - 3 x - 3 m = 0$ 没有实数根，则m的取值范围为．

查看试题解析
6. 如图，有一正方形 $A B C D$ ，边长为4，点E是边 $C D$ 上的中点，对角线 $B D$ 上有一动点F，当顶点为A、B、F的三角形与顶点为D、E、F的三角形相似时， $B F$ 的值为．

查看试题解析

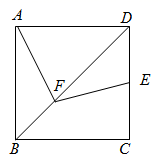
二、单选题

7. 2020年7月23日，中国首颗火星探测器“天问一号”顺利升空，当“天问一号”探测器抵达火星附近时，总飞行里程将达到470000000公里.470000000这个数字用科学记数法表示为（）

A、 $4.7 \times 10^{7}$ B、 $4.7 \times 10^{8}$ C、 $4.7 \times 10^{9}$ D、 $47 \times 10^{7}$

查看试题解析
8. 下列运算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt[3]{9} = 3$ C、 $\sqrt{7} + \sqrt{5} = 2$ D、 ${(- 2 a b^{2})}^{2} = 4 a^{2} b^{4}$

查看试题解析
9. 如图所示的几何体是由7个大小相同的小立方块搭成的，下列说法正确的是（）

A、几何体的主视图与左视图一样 B、几何体的主视图与俯视图一样 C、几何体的左视图与俯视图一样 D、几何体的三视图都一样

查看试题解析
10. 已知某品牌显示器的使用寿命为定值．这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系，图象如图所示．如果这种显示器至少要用2000天，那么显示器平均每天工作的小时数x应控制在（）

A、 $0 < x \leq 10$ B、 $10 \leq x \leq 24$ C、 $0 < x \leq 20$ D、 $20 \leq x \leq 24$

查看试题解析
11. 为宣传和普及垃圾分类的有效方法，不断增强同学们的环保意识，某学校举办了垃圾分类知识竞赛活动．学校为了解学生对这次大赛的掌握情况，在全校1500名学生中随机抽取部分学生进行了一次问卷调查，并根据收集到的信息进行了统计，绘制了两幅统计图，如图所示．下列四个选项错误的是（）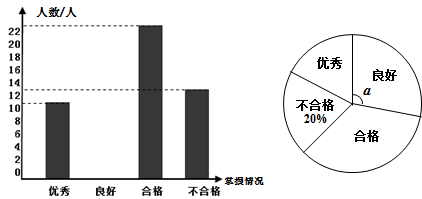

A、样本容量为60 B、所抽取学生中，竞赛成绩“良好”的人数为16人 C、所抽取学生中，成绩为“优秀”和“良好”的人数占比和低于“合格”的人数占比 D、 $α = 96 °$

查看试题解析
12. 如图， $∠ A B C = 30 °$ ，边 $B A$ 上有一点D， $D B = 4$ ，以点D为圆心，以 $D B$ 长为半径作弧交 $B C$ 于点E，则BE=（）

A、 $4 \sqrt{3}$ B、4 C、 $2 \sqrt{3}$ D、8

查看试题解析
13. 下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规律排列下去，当第n个图形中实心圆点的个数为104个时，则n为（）

A、32 B、33 C、34 D、35

查看试题解析
14. 若关于x的一元一次不等式组 ${\begin{array}{l} x + 3 \geq 2 (x - 1) \\ \frac{x - 2 a}{3} < 1 \end{array}$ 的解集为 $x \leq 5$ ，且关于y的分式方程 $\frac{a - 4}{y - 2} + \frac{4}{2 - y} = 1$ 的解为非正数，则符合条件的a所有整数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析

三、解答题

15. 先化简，再求值 $(4 x - \frac{4 x - 1}{x}) \div \frac{2 x - 1}{x}$ ，其中 $x = \sqrt{2} + \frac{1}{2}$ ．

查看试题解析
16. 如图， $A B / / C D$ ，点E是 $A C$ 的中点．

求证： $A B = C D$ ．

查看试题解析

17. 《生物多样性公约》第十五次缔约方大会（COP15）重新确定于2021年5月17日至30日在云南省昆明市举办．“生物多样性”的目标、方法和全球通力合作，将成为国际范围的热点关注内容．为广泛宣传云南生物多样性，某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试．现分别在七、八两个年级中各随机抽取了10名学生，统计这部分学生的竞赛成绩，相关数据统计、整理如下：

（收集数据）

七年级10名同学测试成绩统计如下：

72，84，72，91，79，69，78，85，75，95

八年级10名同学测试成绩统计如下：

85，72，92，84，80，74，75，80，76，82

（整理数据）两组数据各分数段，如下表所示：

成绩	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x < 100$
七年级	1	5	2	a
八年级	0	4	5	1

（分析数据）两组数据的平均数、中位数、众数、方差如下表：

统计量

年级

平均数

中位数

众数

方差

七年级

$S_{七年级}^{2}$

八年级

(1)、（问题解决）根据以上信息，解答下列问题：

填空：a= ， b= ， c=；

(2)、计算八年级同学测试成绩的方差是：

$S_{八年级}^{2} = \frac{1}{10} \times [{(80 - 85)}^{2} + {(80 - 72)}^{2} + {(80 - 92)}^{2} + {(80 - 84)}^{2} + {(80 - 80)}^{2} + {(80 - 74)}^{2} + {(80 - 75)}^{2} + {(80 - 80)}^{2} + {(80 - 76)}^{2} + {(80 - 82)}^{2}] = 33$ 请你求出七年级同学成绩的方差，试估计哪个年级的竞赛成绩更整齐？

(3)、按照比赛规定90分及其以上算优秀，请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人？

(4)、根据以上数据，你认为该校七、八年级中哪个年级学生知识竞赛成绩更好？请说明理由（写出一条理由即可）．

查看试题解析

18. 习近平总书记指出：“扶贫先扶志，扶贫必扶智”．某企业扶贫小组准备在春节前夕慰问贫困户，为贫困户送去温暖．该扶贫小组购买了一批慰问物资并安排两种货车运送．据调查得知，2辆大货车与4辆小货车一次可以满载运输700件；5辆大货车与7辆小货车一次可以满载运输1450件．

(1)、求1辆大货车和1辆小货车一次可以分别满载运输多少件物资？

(2)、计划租用两种货车共10辆运输这批物资，每辆大货车一次需费用5000元，每辆小货车一次需费用3000元．若运输物资不少于1300件，且总费用不超过46000元．请你指出共有几种运输方案，并计算哪种方案所需费用最少，最少费用是多少？

查看试题解析
19. 2020年3月，中共中央、国务院印发了《关于全面加强新时代大中小学劳动教育的意见》（以下简称中央《意见》），就加强大中小学劳动教育进行了系统设计和全面部署.2020年11月，中共云南省委、云南省人民政府全面对照落实中央《意见》精神，结合云南实际，印发了《关于全面加强新时代大中小学劳动教育的实施意见》（以下简称《实施意见》），《实施意见》要求各地各校组织学生广泛开展劳动教育实践活动．昆明甲、乙两校想从下面四个劳动实践基地中任选一个，地点如下：
A：澄江抚仙湖仙湖农场劳动实践教育基地；

B：富民半山耕云劳动实践教育基地；

C：石林杏林大观园中医药文化研学实践教育基地；

D：石林锦苑花卉鲜花种植劳动实践教育基地．

(1)、求甲校选择到澄江抚仙湖仙湖农场劳动实践教育基地的概率；

(2)、甲、乙两校决定通过抽签的方式确定本次开展劳动教育实践活动的目的地，请你用树状图或列表的方法求出两所学校到同一地点开展劳动教育实践活动的概率．

查看试题解析
20. 普洱茶是中国十大名茶之一，也是中华古老文明中的一颗瑰宝．某公司经销某种品牌普洱茶，每千克成本为50元．经市场调查发现：每周销售量y（千克）与销售单价x（元/千克）满足一次函数关系，部分数据如下表所示，

销售单价x（元/千克）

56

65

75

销售量y（千克）

128

110

90

解答下列问题：

(1)、求y与x的函数关系式；

(2)、求这一周销售这种品牌普洱茶获得的利润W元的最大值；

(3)、物价部门规定茶叶销售单价不得高于90元/千克，公司想获得不低于2000元周利润，请计算销售单价范围．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A B / / C D ， A D ⊥ A B ， B C ⊥ A B$ ．将四边形 $A B C D$ 沿 $B F$ 折叠，点C的对称点E落在边 $A D$ 上， $\frac{E F}{B E} = \frac{2}{3} ， A B = 3$ ．

(1)、求证：四边形 $A B C D$ 是矩形；

(2)、求 $B C$ 的长度．

查看试题解析
22. 如图， $△ A C D$ 是⊙O的内接三角形， $A D$ 是⊙O的直径，点B是⊙O上的一点， $\overset{⌢}{A B} = \overset{⌢}{C D}$ ，点E在 $A D$ 的延长线上，射线 $E F$ 经过点C， $∠ E C D = ∠ A C B$ ；

(1)、求证： $E F$ 是⊙O的切线；

(2)、若 $∠ E = 45 ° ， C E = 4$ ，求 $B C$ 的长．

查看试题解析
23. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 经过 $A (4 ， 0) ， B (- 1 ， 0) ， C (0 ， 4)$ 三点．

(1)、求抛物线的函数解析式；

(2)、如图1，点D是在直线 $A C$ 上方的抛物线的一点， $D N ⊥ A C$ 于点N， $D M / / y$ 轴交 $A C$ 于点M，求 $△ D M N$ 周长的最大值及此时点D的坐标；

(3)、如图2，点P为第一象限内的抛物线上的一个动点，连接 $O P$ ， $O P$ 与 $A C$ 相交于点Q，求 $\frac{S_{△ A P Q}}{S_{△ A O Q}}$ 的最大值．

查看试题解析

销售单价x（元/千克）	56	65	75
销售量y（千克）	128	110	90