内蒙古自治区呼和浩特2020年中考数学三模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 检查四个篮球的质量，把超过标准质量的克数记为正数，不足标准质量的克数记为负数，检查的结果如下表：

篮球编号

1号

2号

3号

4号

与标准质量的差(g)

+4

+7

-3

-8

其中最接近标准质量的球是（）

A、1号 B、2号 C、3号 D、4号

查看试题解析
2. 下列计算正确的是（）

A、3a-a=2 B、a²+2a²=3a² C、a⁴·a³=a⁶ D、(a+b)²=a²+b²

查看试题解析
3. 已知某菱形的周长为 $8 c m$ ，高为 $1 c m$ ，则该菱形的面积为（）

A、 $2 c m^{2}$ B、 $4 c m^{2}$ C、 $6 c m^{2}$ D、 $8 c m^{2}$

查看试题解析
4. 已知m≠0，函数y=-mx²+n与y= $\frac{mn}{x}$ 在同一直角坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 中小学时期是学生身心变化最为明显的时期，这个时期孩子们的身高变化呈现一定的趋势，7~15岁期间生子们会经历一个身高发育较迅速的阶段，我们把这个年龄阶段叫做生长速度峰值段，小明通过上网查阅《2016年某市儿童体格发育调查表》，了解某市男女生7~15岁身高平均值记录情况，并绘制了如下统计图，并得出以下结论：
①10岁之前，同龄的女生的平均身高一般会略高于男生的平均身高；

②10~12岁之间，女生达到生长速度峰值段，身高可能超过同龄男生；

③7~15岁期间，男生的平均身高始终高于女生的平均身高；

④13~15岁男生身高出现生长速度峰值段，男女生身高差距可能逐渐加大．

以上结论正确的是（）

A、①③ B、②③ C、②④ D、③④

查看试题解析
6. 如图是某几何体的三视图，根据图中的数据，求得该几何体的体积为（）

A、175π＋450 B、700π＋450 C、700π＋1500 D、250π＋1050

查看试题解析
7. 已知 $x 、 y$ 关于的二元一次方程组 ${\begin{array}{l} x - y = a + 3 \\ 2 x + y = 5 a \end{array}$ 的解满足 $x > y$ ，且关于x的不等式组 ${\begin{array}{l} 2 x + 1 < 2 a \\ \frac{2 x - 1}{14} \geq \frac{3}{7} \end{array}$ 无解，那么所有符合条件的整数a的个数为（）

A、6个 B、7个 C、8个 D、9个

查看试题解析
8. 以下四个命题：
①如果三角形的三个内角的度数比是3：4：5，那么这个三角形是直角三角形；

②在实数-7.5， $\sqrt{15}$ ，4， $\sqrt[3]{- 27}$ ，-π，( $\sqrt{2}$ )²中，有4个有理数，2个无理数；

③有一个圆锥，与底面圆直径是 $\sqrt{3}$ 且体积为 $\frac{\sqrt{3} π}{2}$ 的圆柱等高，如果这个圆锥的侧面展开图是半圆，那么它的母线长为 $\frac{4}{3}$ ；

④二次函数 $y = a x^{2} - 2 a x + 1$ ，自变量的两个值x₁ ， x₂对应的函数值分别为y₁ ， y₂ ，若|x₁-1|>|x₂-1|，则a(y₁-y₂)>0．

其中正确的命题的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在平面直角坐标系中，四边形ABCD是平行四边形，A（－1，3）、B（1，1）、C（5，1）．规定“把▱ABCD先沿x轴翻折，再向左平移1个单位”为一次变换．如此这样，连续经过2018次变换后，▱ABCD的顶点D的坐标变为（）

A、（－2015，3） B、（－2015，－3） C、（－2016，3） D、（－2016，－3）

查看试题解析
10. 如图，线段 $A B$ 是⊙ $O$ 的直径，弦 $C D ⊥ A B$ ，垂足为 $H$ ，点 $M$ 是 $\overset{⌢}{C B D}$ 上任意一点， $A H = 2 ， C H = 4$ ，则 $\cos ∠ C M D$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题

11. 分解因式：9abc-3a $c^{2}$ 的公因式为，分解因式的结果为．

查看试题解析

12. 某瓷砖厂在相同条件下抽取部分瓷砖做耐磨实验，结果如下表所示：

抽取瓷砖数n	100	300	400	600	1000	2000	3000
合格品数m	96	282	382	570	949	1906	2850
合格品频率 $\frac{m}{n}$	0.960	0.940	0.955	0.950	0.949	0.953	0.950

则这个厂生产的瓷砖是合格品的概率估计值是．（精确到0.01）

查看试题解析

13. 有10张卡片，分别写有0~9共10个数字，将背面朝上洗匀后，任意抽出一张，那么P(抽到的数是偶数)= ， P(抽到的数字是3的整数倍)= ．

查看试题解析
14. 如图，在正方形ABCD中，BE平分∠CBD，EF⊥BD于点F，若DE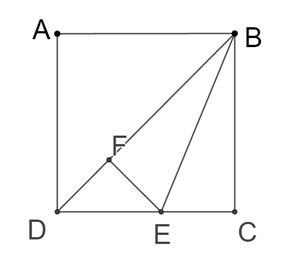= $\sqrt{2}$ ，则BC的长为．

查看试题解析
15. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切(我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形)．若设T₁ ， T₂的边长分别为a，b，圆O的半径为r，则r：a=；r：b=；正六边形T₁ ， T₂的面积比S₁：S₂的值是．

查看试题解析
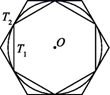16. 如图，Rt△ABC中，∠ACB＝90°，AC＝BC＝4，D为线段AC上一动点，连接BD，过点C作CH⊥BD于H，连接AH，则AH的最小值为.

查看试题解析

三、解答题

17.

(1)、计算：2^-1+ $\sqrt{3}$ cos30°+|-5|-(π-2021)⁰；

(2)、若关于x的方程2x-m=3(x-1)的解也是不等式组 ${\begin{array}{l} 2 x- 1 > 3 x- 2 \\ \frac{x- 1}{2} - 1 \leq x \end{array}$ 的解，求m的取值范围．

查看试题解析
18. 如图，已知AC平分∠BAD ， CE⊥AB于E ， CF⊥AD于F ，且BC＝CD ．

(1)、求证：△BCE≌△DCF；

(2)、若AB＝21，AD＝9，BC＝CD＝10，求AC的长．

查看试题解析
19. 如图，要测量小山上电视塔BC的高度，在山脚下点A测得：塔顶B的仰角为∠BAD=40°，塔底C的仰角为∠CAD=30°，AC=200米，求电视塔BC的高．（结果用含非特殊角的锐角三角函数及根式表示即可）

查看试题解析

20. 为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

(1)、活动启动之初学生“一周诗词诵背数量”的中位数为；

(2)、估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

(3)、选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

查看试题解析

21. 如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A（ $\frac{3}{2}$ ，﹣2），反比例函数y= $\fr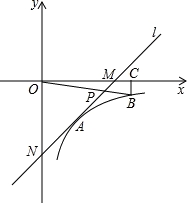ac{k}{x}$ （x＞0）的图象过点A．

(1)、求直线l的解析式；

(2)、在函数y= $\frac{k}{x}$ （x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．

查看试题解析
22. 为了防控新冠肺炎，某校积极进行校园环境消毒，第一次购买甲、乙两种消毒液分别用了240元和540元，每瓶乙种消毒液的价格是每瓶甲种消毒液价格的 $\frac{3}{2}$ ，购买的乙种消毒液比甲种消毒液多20瓶．

(1)、求甲、乙两种消毒液每瓶各多少元？

(2)、该校准备再次购买这两种消毒液，使再次购买的乙种消毒液瓶数是甲种消毒液瓶数的一半，且再次购买的费用不多于1050元，求甲种消毒液最多能再购买多少瓶？

查看试题解析
23. 如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E，过点D作FG⊥AC于点F，交AB的延长线于点G．

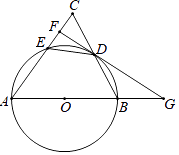(1)、求证：FG是⊙O的切线；

(2)、若tanC=2，求 $\frac{G B}{G A}$ 的值．

查看试题解析
24. 如图，一次函数y=kx+2的图象分别交y轴，x轴于A，B两点，且tan∠ABO= $\frac{1}{2}$ ，抛物线y=-x²+bx+c经过A，B两点．

(1)、求k的值及抛物线的解析式．

(2)、直线x=t在第一象限交直线AB于点M，交抛物线于点N，当t取何值时，线段MN的长有最大值？最大值是多少？

(3)、在（2）的情况下，以A，M，N，D为顶点作平行四边形，求第四个顶点D的坐标，并直接写出所有平行四边形的面积，判断面积是否都相等．

查看试题解析

篮球编号	1号	2号	3号	4号
与标准质量的差(g)	+4	+7	-3	-8