云南省曲靖市师宗县2020年中考数学一模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、填空题
-
1. 函数 自变量x的取值范围是 .2. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .3. 在如图所示的电路中,随机闭合开关S1 , S2 , S3中的两个,能让灯泡L1发光的概率是 .
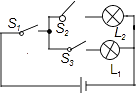 4. 用半径为12cm,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 cm.5. 如图,PA 、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在 上,若PA长为2,则△PEF的周长是 .
4. 用半径为12cm,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为 cm.5. 如图,PA 、PB分别与⊙O相切于点A、B,⊙O的切线EF分别交PA、PB于点E、F,切点C在 上,若PA长为2,则△PEF的周长是 .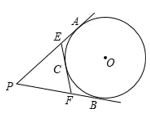 6. 二次函数y= 的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
6. 二次函数y= 的图象如图,点A0位于坐标原点,点A1 , A2 , A3…An在y轴的正半轴上,点B1 , B2 , B3…Bn在二次函数位于第一象限的图象上,点C1 , C2 , C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1 , 四边形A1B2A2C2 , 四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn=60°,菱形An﹣1BnAnCn的周长为 .
二、单选题
-
7. 下列生态环保标志中,是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 8. 从﹣5, , ,﹣1,0,2,π这七个数中随机抽取一个数,恰好为无理数的概率为( )A、 B、 C、 D、9. 如图,四边形ABCD是 的内接四边形,若 ,则 的度数是
8. 从﹣5, , ,﹣1,0,2,π这七个数中随机抽取一个数,恰好为无理数的概率为( )A、 B、 C、 D、9. 如图,四边形ABCD是 的内接四边形,若 ,则 的度数是 A、 B、 C、 D、10. 若α、β是一元二次方程x2+2x﹣6=0的两根,则 的值是( )A、 B、 C、﹣3 D、311. 某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )A、10% B、15% C、20% D、25%12. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、
A、 B、 C、 D、10. 若α、β是一元二次方程x2+2x﹣6=0的两根,则 的值是( )A、 B、 C、﹣3 D、311. 某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长率为( )A、10% B、15% C、20% D、25%12. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、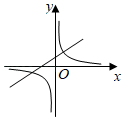 B、
B、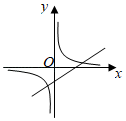 C、
C、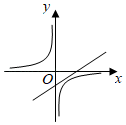 D、
D、 13. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
13. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b+c<0.其中正确的个数有( )
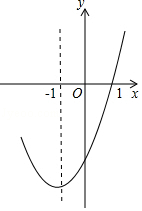 A、2 B、3 C、4 D、514. 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
A、2 B、3 C、4 D、514. 如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )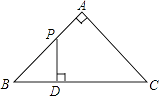 A、
A、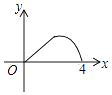 B、
B、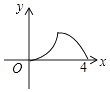 C、
C、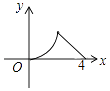 D、
D、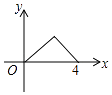
三、解答题
-
15. 解方程(1)、 ;(2)、 .16. 如图,在平面直角坐标系中,已知
 ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4). 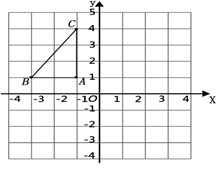
⑴画出△ABC关于y轴对称的图形;
⑵将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留
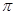 )17. 已知关于x的方程x2﹣(2k+1)x+4(k﹣ )=0(1)、求证:无论k取何值,这个方程总有实数根;(2)、若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.18. 如图,在 中, , ,D是AB边上一点 点D与A,B不重合 ,连结CD,将线段CD绕点C按逆时针方向旋转 得到线段CE,连结DE交BC于点F,连接BE.
)17. 已知关于x的方程x2﹣(2k+1)x+4(k﹣ )=0(1)、求证:无论k取何值,这个方程总有实数根;(2)、若等腰三角形ABC的一边长a=4,另两边b、c恰好是这个方程的两个根,求△ABC的周长.18. 如图,在 中, , ,D是AB边上一点 点D与A,B不重合 ,连结CD,将线段CD绕点C按逆时针方向旋转 得到线段CE,连结DE交BC于点F,连接BE.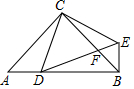 (1)、求证: ≌ ;(2)、当 时,求 的度数.19. 在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两个球上的数字之和,当和小于9时小明获胜,反之小东获胜.(1)、请用树状图或列表的方法,求小明获胜的概率;(2)、这个游戏公平吗?请说明理由.20. 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a , b为常数,且a≠0)与反比例函数y2= (m为常数,且m≠0)的图象交于点A(﹣2,1),B(1,n).
(1)、求证: ≌ ;(2)、当 时,求 的度数.19. 在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两个球上的数字之和,当和小于9时小明获胜,反之小东获胜.(1)、请用树状图或列表的方法,求小明获胜的概率;(2)、这个游戏公平吗?请说明理由.20. 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a , b为常数,且a≠0)与反比例函数y2= (m为常数,且m≠0)的图象交于点A(﹣2,1),B(1,n).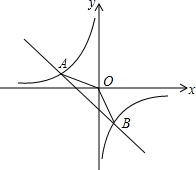 (1)、求反比例函数和一次函数的解析式;(2)、连接OA , OB , 求△AOB的面积;(3)、直接写出当y1>y2时,自变量x的取值范围.21. 大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.(1)、求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?(3)、利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?22. 如图,AB为⊙O的直径,CB , CD分别切⊙O于点B , D , CD交BA的延长线于点E , CO的延长线交⊙O于点G , EF⊥OG于点F .
(1)、求反比例函数和一次函数的解析式;(2)、连接OA , OB , 求△AOB的面积;(3)、直接写出当y1>y2时,自变量x的取值范围.21. 大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨x元(x为非负整数),每个月的销售利润为y元.(1)、求y与x的函数关系式,并直接写出自变量x的取值范围;(2)、利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?(3)、利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?22. 如图,AB为⊙O的直径,CB , CD分别切⊙O于点B , D , CD交BA的延长线于点E , CO的延长线交⊙O于点G , EF⊥OG于点F . (1)、求证:∠FEB=∠ECF;(2)、若BC=6,DE=4,求EF的长.23. 如图,直线y=﹣x+3与x轴、y轴分别交于点B , 点C , 经过B , C两点的抛物线y=x2+bx+c与x轴的另一个交点为A , 顶点为P , 点M为抛物线的对称轴上的一个动点.
(1)、求证:∠FEB=∠ECF;(2)、若BC=6,DE=4,求EF的长.23. 如图,直线y=﹣x+3与x轴、y轴分别交于点B , 点C , 经过B , C两点的抛物线y=x2+bx+c与x轴的另一个交点为A , 顶点为P , 点M为抛物线的对称轴上的一个动点.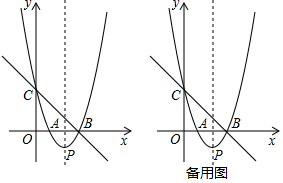 (1)、求该抛物线的解析式;(2)、当点M在x轴的上方时,求四边形COAM周长的最小值;(3)、在平面直角坐标系内是否存在点N , 使以C , P , M , N为顶点的四边形为菱形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、当点M在x轴的上方时,求四边形COAM周长的最小值;(3)、在平面直角坐标系内是否存在点N , 使以C , P , M , N为顶点的四边形为菱形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.