山西省临汾市尧都区九2020年中考数学三模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 已知∠A＝80°，则∠A的补角是（　　）

A、100° B、80° C、40° D、10°

查看试题解析
2. 下列运算正确的是（）

A、 $x^{3} + x^{2} = x^{5}$ B、 $x^{3} \cdot x^{2} = x^{6}$ C、 ${(- x^{3})}^{2} \div x^{5} = 1$ D、 ${(- x)}^{3} \div {(- x)}^{2} = - x$

查看试题解析
3. 如图，A ， B两地被池塘隔开，小明先在直线AB外选一点C ，然后步测出AC ， BC的中点M ， N ，并步测出MN的长为6.5m ．由此，他可以知道A ． B间的距离为（　　）

A、12m B、12.5m C、13m D、13.5m

查看试题解析

4. 某体校要从四名射击选手中选拔一名选手参加省体育运动会，选拔赛中每名选手连续射靶10次，他们各自的平均成绩及其方差如下表所示：

	甲	乙	丙	丁
$\bar{x}$ （环）	$8.6$	$8.4$	$8.6$	$7.6$
$x^{2}$	$0.56$	$0.74$	$0.94$	$1.92$

如果要选出一名成绩高且发挥稳定的选手参赛，则应选择的选手是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

5. 如图，AC是⊙O的直径，B ， D是⊙O上的点，且∠CAB＝34°，则∠D的度数是（　　）

A、44° B、54° C、56° D、66°

查看试题解析
6. 探究课上，老师给出一个问题“利用二次函数y＝2x²与一次函数y＝x+2的图象，求一元二次方程2x²＝x+2的近似根”小华利用计算机绘制出如图所示的图象，通过观察可知该方程的两近似根x₁和x₂满足﹣1＜x₁＜0，1＜x₂＜2．小华的上述方法体现的数学思想是（　　）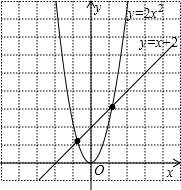

A、公理化 B、分类讨论 C、数形结合 D、由特殊到一般

查看试题解析
7. 在一个不透明的袋中，装有2个黄球和3个红球，它们除颜色外都相同．从袋中任意摸出两个球，则这两个球颜色不同的概率是（　　）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{4}{5}$ D、 $\frac{1}{5}$

查看试题解析
8. 某种品牌自行车的进价为400元，出售时标价为500元，商店准备打折出售，但要保持利润率不低于5%，则至多可打的折数是（　　）

A、八折 B、八四折 C、八五折 D、八八折

查看试题解析
9. 如图，在平面直角坐标系中，第二象限内的点P是反比例函数y＝ $\frac{k}{x}$ （k≠0）图象上的一点，过点P作PA⊥x轴于点A ，点B为AO的中点若△PAB的面积为3，则k的值为（　　）

A、6 B、﹣6 C、12 D、﹣12

查看试题解析
10. 如图，正方形ABCD的边长为2，点O为其中心．将其绕点O顺时针旋转45°后得到正方形A'B'C'D'，则旋转前后两正方形重叠部分构成的多边形的周长为（　　）（参考计算： $\frac{1}{2 + \sqrt{2}} = \frac{2 - \sqrt{2}}{2} ， \frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ）

A、16﹣8 $\sqrt{2}$ B、16 $\sqrt{2}$ ﹣16 C、12﹣8 $\sqrt{2}$ D、16 $\sqrt{2}$ ﹣12

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} x - 2 > - 3, \\ 12 (x - 2) \geq 3 x - 6 \end{array}$ 的解集是．

查看试题解析
12. 如图是一组有规律的图案，它们是由边长相同的正方形和等边三角形组成，其中正方形涂有阴影．依此规律，第n个图案中有个涂有阴影的正方形（用含有n的代数式表示）．

查看试题解析
13. 盈不足术是中国古代解决盈亏类问题的一种算术方法．中国古代数学名著《九章算术》中，专辟一章名为“盈不足”．该章第一个问题大意是“有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元．问该物品售价为多少元？”，则该物品售价为元．

查看试题解析
14. 某兴趣小组同学借助无人机航拍测量某公园内一座古塔高度．如图，无人机在距离地面168米的A处，测得该塔底端点B的俯角为40°，然后向古塔方向沿水平面飞行50秒到达点C处，此时测得该塔顶端点D的俯角为60°．已知无人机的飞行速度为3米/秒，则这座古塔的高度约为米（参考计算：sin40°≈064．cos40°≈077．tan40°≈0.84. $\sqrt{2}$ ≈1.41. $\sqrt{3} \approx$ 1.73．结果精确到0.1米）

查看试题解析
15. 如图，平行四边形ABCD的边长AD＝3，AB＝2，∠BAD＝120°，E为AB的中点，F在边BC上，且BF＝2FC ． AF与DE交于点G ，则AG的长为．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{18} - | - 4 |$ |+（ $\frac{1}{3}$ ）^﹣2﹣4 $\sqrt{\frac{1}{2}}$

(2)、化简： $\frac{x^{2} - 4 x + 4}{x^{2} - 4} \div \frac{x - 2}{x^{2} + 2 x}$

查看试题解析

17. 截至2019年5月，山西省政府大力实施的建设“山西农谷”战略成果初现，“山西农谷”通过组建山西农谷生物科技研究院，逐步建成大学生“互联网+农业”创新创业园．某校科技小组到该创业园的全环境智能番茄特色小镇进行综合实践活动，随机调查了60株“农谷一号“番茄的挂果数量（单位：个），并绘制了如下不完靠的统计图表：

“农谷一号”番茄挂果数量统计表

挂果数量x（个）	频数（株）	频率
25≤＜35	6
35≤x＜45		0.2
45≤x＜55	15	a
55≤x＜65
65≤x＜75	9

请结合图表中的信息解答下列问题：

(1)、统计表中，a＝，若绘制“农谷一号”番茄挂果数量扇形统计图，则挂果数量在“35≤x＜45”所对应扇形的圆心角度数为；

(2)、将频数分布直方图补充完整；

(3)、若所种植的“农谷一号”番茄有1000株，请估计挂果数量在“55≤x＜65”范围的番茄株数．

查看试题解析

18. 如图，在平面直角坐标系中，菱形ABCD的顶点B ， C在x轴上，反比例函数y＝﹣ $\frac{4}{x}$ （x＜0）的图象经过A ， E两点，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过第一象限内的D ， H两点，正方形EFCH的顶点F ． G在AD上．已知A（﹣1，a），B（﹣4，0）．

(1)、求点C的坐标及k的值；

(2)、直接写出正方形EFGH的边长．

查看试题解析
19. 阅读与探究
请阅读下列材料，完成相应的任务：幻方：将若干个数组成一个正方形数阵，若任意一行，一列及对角线上的数字之和都相等，则称具有这种性质的数字方阵为“幻方”．中国古代称“幻方”为“河图”“洛书”等，例如，图1是一个三阶幻方，是将数字1，2，3，4，5，6，7，8，9填入到3x3的方格中得到的，其每行、每列、每条对角线上的三个数之和相等，我们称这种幻方为“数字连续型三阶幻方”．

(1)、任务：
观察图1中三阶幻方中间的数字与9个数的和，可以发现二者有确定的数量关系．设“数字连续型三阶幻方中间的数字是x ，幻方中9个数的和为s ，则s与x之间的数量关系为；

(2)、现要用9个数3，4，5，6，7，8，9，10，11构造一个三阶幻方．请将构造的幻方填写在图2的3×3方格中；

(3)、某学习小组同学在研究图1的三阶幻方时，发现任何一个角上的数都有两个数与其不在同一行、列及对角线上，并且它们之间存在一个等量关系．为此该小组同学绘制了图3，请你用图3中的字母m ， a ， b表示他们发现的这个等量关系．（直接写出，不必证明）

查看试题解析
20. 如图，以 $A B$ 为直径，点O为圆心的半圆上有一点 $C ，$ 且 $∠ A B C = 60 ° ，$ 点D为 $A O$ 上一点．将 $△ D B C$ 沿直线 $D C$ 对折得到 $△ D B' C ，$ 点B的对应点为 $B^{'} ，$ 且 $B' C$ 与半圆相切于点 $C ，$ 连接 $B' O$ 交半圆于点E．

(1)、求证： $B' D ⊥ A B$ ；

(2)、当 $A B = 2$ 时，求图中阴影部分面积．

查看试题解析
21. 某书店积极响应政府“改革创新，奋发有为”的号召，举办“读书节“系列活动．活动中故事类图书的标价是典籍类图书标价的1.5倍，若顾客用540元购买图书，能单独购买故事类图书的数量恰好比单独购买典籍类图书的数量少10本．

(1)、求活动中典籍类图书的标价；

(2)、该店经理为鼓励广大读者购书，免费为购买故事类的读者赠送图1所示的精致矩形包书纸．在图1的包书纸示意图中，虚线是折痕，阴影是裁剪掉的部分，四角均为大小相同的正方形，正方形的边长为折叠进去的宽度．已知该包书纸的面积为875cm²（含阴影部分），且正好可以包好图2中的《中国故事》这本书，该书的长为21cm ，宽为15cm ，厚为1cm ，请直接写出该包书纸包这本书时折叠进去的宽度．

查看试题解析
22. 综合与实践
问题情境

在综合与实践课上，老师组织同学们以“三角形纸片的旋转”为主题开展数学活动．如图1，现有矩形纸片ABCD ， AB＝4cm ， AD＝3cm ．连接BD ，将矩形ABCD沿BD剪开，得到△ABD和△BCE ．保持△ABD位置不变，将△BCE从图1的位置开始，绕点B按逆时针方向旋转，旋转角为α（0°≤α＜360°）．

(1)、操作发现
在△BCE旋转过程中，连接AE ， AC ，则当α＝0°时， $\frac{A C}{A E}$ 的值是；

(2)、如图2，将图1中的△BCE旋转，当点E落在BA延长线上时停止旋转，求出此时的 $\frac{A C}{A E}$ 值；

(3)、实践探究
如图3，将图2中的△BCE继续旋转，当AC＝AE时停止旋转，直接写出此时α的度数，并求出△AEC的面积；

(4)、将图3中的△BCE继续旋转，则在某一时刻AC和AE还能相等吗？如果不能，则说明理由；如果能，请在图4中画出此时的△BCE ，连接AC ， AE ，并直接写出△AEC的面积值．

查看试题解析
23. 综合与探究
如图1，在平面直角坐标系中，抛物线y＝ax²+ $\frac{8}{3}$ x+3与x轴交于A ， B两点（A在B左侧），与y轴交于点C ．点A坐标为（﹣1，0）．直线l为该抛物线的对称轴，且交直线BC于点D ．抛物线上有一动点P ，且横坐标为m（4＜m＜9），连接PD ，过点P作PE⊥l于点E ．

(1)、求抛物线及直线BC的函数表达式．

(2)、当△DEP与△BOC相似时，求m的值；

(3)、如图2，点M为直线BC上一动点，是否存在点P ，使得以点A ， C ， P ． M为顶点的四边形是平行四边形？若存在，直接写出此时点P和点M的坐标；若不存在，说明理由．

查看试题解析