山东省济宁市汶上县2020年中考数学二模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

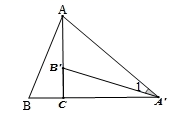
1. ﹣2的绝对值等于（）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、±2

查看试题解析
2. 下列运算正确的是（）．

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $x^{3} \cdot x^{2} = x^{5}$ C、 ${(x^{3})}^{2} = x^{5}$ D、 $x^{6} \div x^{2} = x^{3}$

查看试题解析
3. 某校为了了解家长对“禁止学生带手机进入校园”这一规定的意见，随机对全校100名学生家长进行调查，这一问题中样本是（）

A、100 B、被抽取的100名学生家长 C、被抽取的100名学生家长的意见 D、全校学生家长的意见

查看试题解析
4. 中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两(我国古代货币单位)；马三匹、牛五头，共价三十八两．问马、牛各价几何?”设马每匹 $x$ 两，牛每头 $y$ 两，根据题意可列方程组为（）

A、 ${\begin{cases} 4 x + 6 y = 38 \\ 3 x + 5 y = 48 \end{cases}$ B、 ${\begin{cases} 4 y + 6 x = 48 \\ 3 y + 5 x = 38 \end{cases}$ C、 ${\begin{cases} 4 x + 6 y = 48 \\ 5 x + 3 y = 38 \end{cases}$ D、 ${\begin{cases} 4 x + 6 y = 48 \\ 3 x + 5 y = 38 \end{cases}$

查看试题解析
5. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A'B'C ，连接AA'，若∠1=25°，则∠BAA'的度数是(　　)

A、70° B、65° C、60° D、55°

查看试题解析
6. 如图是抛物线 $y = {ax}^{2} + bx + c (a \neq 0)$ 图象的一部分．当 $y < 0$ 时，自变量x的范围是（）

A、 $x < - 1$ 或 $x > 2$ B、 $x < - 1$ 或 $x > 5$ C、 $- 1 < x < 5$ D、 $- 1 < x < 2$

查看试题解析
7. 如图，Rt△AOB中，∠AOB=90°，顶点A ， B分别在反比例函数 $y = \frac{1}{x}$ ( $x >0$ )与 $y = \frac{- 5}{x}$ ( $x <0$ )的图象上，则tan∠BAO的值为(　　)

A、1 B、2 C、3 D、 $\sqrt{5}$

查看试题解析
8. 如图，在直角坐标系中，点A(0，3)、点B(4，3)、点C(0，-1)，则△ABC外接圆的半径为(　　)

A、2 B、3 C、4 D、 $2 \sqrt{2}$

查看试题解析
9. 2015年4月份的尼泊尔强震曾经导致珠峰雪崩，在珠峰抢险时，需8组登山队员步行运送物资，要求每组分配的人数相同，若按每组人数比预定人数多分配1人，则总数会超过100人；若按每组人数比预定人数少分配1人，则总数不够90人，那么预定每组分配的人数是(　　)

A、10 B、11 C、12 D、13

查看试题解析
10. 如图，在□ABCD中， $M$ 是 $A B$ 上一点，且 $A M ： M B = 2 ： 3$ ， $A C$ 与 $D M$ 交于点 $N$ ，若 $Δ A M N$ 的面积是1 ，则□ABCD的面积是：（）

A、16.5 B、17.25 C、17.5 D、18.75

查看试题解析

二、填空题

11. 计算： ${(π - 3)}^{0} + \sqrt{4}$ = ．

查看试题解析
12. 如果一次函数 $y = k x - 2 (k$ 是常数， $k \neq 0)$ 的图象经过点 $(2, 0)$ ，那么y的值随x的增大而 $($ 填“减小”或“增大” $)$

查看试题解析
13. 如图，在平面直角坐标系中，已知A（1.5，0），D（4.5，0），△ABC与△DEF位似，原点O是位似中心．若DE＝7.5，则AB＝．

查看试题解析
14. 在 $△ A B C$ 中，AD是BC边上的高， $B C = 12$ ， $A D = 8.$ 正方形EFGH的顶点E、F分别在AB、AC上，H、G在BC上．那么正方形EFGH的边长是．

查看试题解析
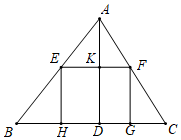15. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} - 2 a x + \frac{8}{3} (a > 0)$ 与y轴交于点A，过点A作x轴的平行线交抛物线于点M．P为抛物线的顶点．若直线OP交直线AM于点B，且M为线段AB的中点，则a的值为．

查看试题解析

三、解答题

16. 先化简，再求值： $（ \frac{x}{x - 2} - \frac{1}{x - 2}) \div \frac{x - 1}{x^{2} - 4}$ ，其中 $x = 3$ ．

查看试题解析
17. 如今很多初中生购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：
A：自带白开水；B：瓶装矿泉水；C：碳酸饮料；D：非碳酸饮料．

根据统计结果绘制如下两个统计图（如图），根据统计图提供的信息，解答下列问题：

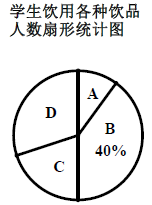(1)、请你补全条形统计图；

(2)、在扇形统计图中，求“碳酸饮料”所在的扇形的圆心角的度数；

(3)、为了养成良好的生活习惯，班主任决定在自带白开水的5名同学（男生2人，女生3人）中随机抽取2名同学担任生活监督员，请用列表法或树状图法求出恰好抽到一男一女的概率．

查看试题解析
18. 知识改变世界，科技改变生活，导航装备的不断更新极大方便了人们的出行.周末，小强一家到 $B ， C$ 两处景区游玩，他们从家 $A$ 处出发，向正西行驶160 $k m$ 到达 $B$ 处，测得 $C$ 处在 $B$ 处的北偏西15°方向上，出发时测得 $C$ 处在 $A$ 处的北偏西60°方向上

(1)、填空： $∠ C =$ 度；

(2)、求 $B$ 处到 $C$ 处的距离即 $B C$ 的长度（结果保留根号）

查看试题解析

19. 水产公司有一种海产品共2104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：

	第1天	第2天	第3天	第4天	第5天	第6天	第7天	第8天
售价x(元/千克)	400	300	250	240	200	150	125	120
销售量y(千克)	30	40	48	50	60	80	96	100

观察表中数据，发现可以用反比例函数刻画这种海产品每天的销售量y(千克)与销售价格x(元/千克)之间的关系．现假定在这批海产品的销售中，每天的销售量y(千克)与销售价格x(元/千克)之间都满足这一关系．

(1)、写出这个反比例函数的解析式；

(2)、在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下的这些海产品预计再用多少天可以全部售出？

(3)、在按（2）中定价继续销售15天后，公司发现剩余的这些海产品必须在不超过2天内全部售出，此时需要重新确定一个销售价格，使后面两天都按新的价格销售，那么新确定的价格最高不超过每千克多少元才能完成销售任务？

查看试题解析

20. （阅读理解）
我们将使得函数值为零的自变量的值称为函数的零点值，此时的点称为函数的零点．例如，对于函数y=x-1，令y=0，可得x=1，我们就说1是函数y=x-1的零点值，点(1，0)是函数y=x-1的零点．

(1)、（问题解决）
已知函数 $y = \frac{3}{x} - 1$ ，则它的零点坐标为；

(2)、若二次函数y=x²－2x＋m有两个零点，则实数m的取值范围是；

(3)、已知二次函数 $∠$ 的两个零点都是整数点，求整数k的值．

查看试题解析
21. 如图1，圆内接四边形ABCD，AD＝BC，AB是⊙O的直径．

(1)、求证：AB∥CD；

(2)、如图2，连接OD，作∠CBE＝2∠ABD，BE交DC的延长线于点E，若AB＝6，AD＝2，求CE的长；

(3)、如图3，延长OB使得BH＝OB，DF是⊙O的直径，连接FH，若BD＝FH，求证：FH是⊙O的切线．

查看试题解析
22. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = - 1$ ，且抛物线与 $x$ 轴交于 $A$ 、 $B$ 两点，与 $y$ 轴交于 $C$ 点，其中 $A (1 ， 0)$ ， $C (0 ， 3)$ .

(1)、若直线 $y = m x + n$ 经过 $B$ 、 $C$ 两点，求直线 $B C$ 和抛物线的解析式；

(2)、在抛物线的对称轴 $x = - 1$ 上找一点 $M$ ，使点 $M$ 到点 $A$ 的距离与到点 $C$ 的距离之和最小，求出点 $M$ 的坐标；

(3)、设点 $P$ 为抛物线的对称轴 $x = - 1$ 上的一个动点，求使 $Δ B P C$ 为直角三角形的点 $P$ 的坐标.

查看试题解析