山东省济宁市泗水县2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. -3的绝对值是( )A、﹣3 B、3 C、±3 D、﹣|﹣3|2. 在平面直角坐标系xOy中,点A的坐标为(-2,1),则点A关于x轴的对称点的坐标为( )A、(-2,-1) B、(2,-1) C、(2, 1) D、(-1,2)3. 下列调查中,最适宜采用全面调查方式的是( )A、对全国初中学生视力状况的调查 B、对“国庆”期间全国居民旅游出行方式的调查 C、新冠疫情期间旅客上飞机前的体温监测 D、了解某种品牌手机电池的使用寿命4. 如图是由10个同样大小的小正方体摆成的几何体.将小正方体①移走后,则关于新几何体的三视图不发生改变的是( )
 A、主视图 B、左视图 C、俯视图 D、主视图、左视图都不改变5. 泰山风景区推出“ 智慧泰山”, 是未来社会的基础设施,是国家战略. 网络峰值速率是 网络峰值速率的10倍,在峰值速率下传输1000兆数据, ;网络比 网络快约90秒,求这两种网络的蜂值速率,设 网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、6. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A、主视图 B、左视图 C、俯视图 D、主视图、左视图都不改变5. 泰山风景区推出“ 智慧泰山”, 是未来社会的基础设施,是国家战略. 网络峰值速率是 网络峰值速率的10倍,在峰值速率下传输1000兆数据, ;网络比 网络快约90秒,求这两种网络的蜂值速率,设 网络的峰值速率为每秒传输x兆数据,依题意,可列方程是( )A、 B、 C、 D、6. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( ) A、1:3 B、1:4 C、1:5 D、1:257. 定义运算:a★b=a(1-b).若a,b是方程 的两根,则b★b-a★a的值为( )A、0 B、1 C、2 D、与m有关8. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A、1:3 B、1:4 C、1:5 D、1:257. 定义运算:a★b=a(1-b).若a,b是方程 的两根,则b★b-a★a的值为( )A、0 B、1 C、2 D、与m有关8. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( ) A、
A、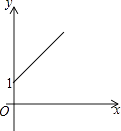 B、
B、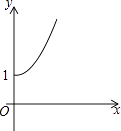 C、
C、 D、
D、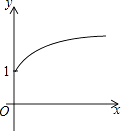 9.
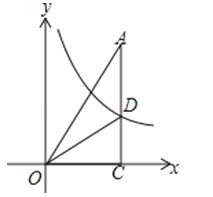
9.如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC的中点D,S△AOC=3,则k=( )
 A、2 B、4 C、6 D、310. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N , 连按EN、EF , 有以下结论:
A、2 B、4 C、6 D、310. 如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N , 连按EN、EF , 有以下结论:①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时, ;④BE+DF=EF . 其中正确的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 计算 的结果是.12. 不等式组 的整数解是.13. 泗水泗河大桥采用H型塔型斜拉桥结构(如甲图),图乙是从图甲抽象出的平面图.测得拉索AB与水平桥面的夹角是45°,拉索CD与水平桥面的夹角是65°,两拉索顶端的距离AC为2米,两拉索底端距离BD为10米,则立柱AH的长是米(结果精确到0.1米).(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
 14. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE , 将 沿 折叠,点C的对应点 恰好落在边 上,则m的值为 .
14. 如图,在矩形 中, , ,点E在边CD上,且 .连接BE , 将 沿 折叠,点C的对应点 恰好落在边 上,则m的值为 . 15. 已知整数 、 、 、 、……满足下列条件: , , , ,……, (n为正整数)依此类推,则 的值为 .
15. 已知整数 、 、 、 、……满足下列条件: , , , ,……, (n为正整数)依此类推,则 的值为 .三、解答题
-
16. 先化简,再求值.(2x+3)(2x﹣3)﹣4x(x+1)-(x﹣2)2 , 其中x=﹣ .17. 运动对学生的成长有着深远的影响,某中学为了解学生每天运动的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别
时间/时
频数/人数
频率
A
0≤t≤0.5
8
0.16
B
0.5≤t≤1
a
0.3
C
1≤t≤1.5
16
0.32
D
1.5≤t≤2
7
b
E
2≤t≤2.5
4
0.08
合计
1

请根据图表中的信息,解答下列问题:
(1)、表中的a= , b= , 中位数落在组,并补全频数分布直方图;(2)、估计该校3000名学生中,每天运动时间不足0.5小时的学生大约有多少名?(3)、已知E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出2人向全校同学作运动心得报告,请用画树状图或列表法求抽取的2名学生刚好是1名男生和1名女生的概率.18. 如图,在矩形ABCD中,E是CD边上的点,且BE=BA,以点A为圆心、AD长为半径作⊙A交AB于点M,过点B作⊙A的切线BF,切点为F. (1)、请判断直线BE与⊙A的位置关系,并说明理由;(2)、如果AB=10,BC=5,求图中阴影部分的面积.19. 某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A , B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.(1)、求这两种马路清扫车的单价;(2)、若该公司承包的道路清扫面积为118000m2 , 每辆A型马路清扫车每天清扫5000m2 , 每辆B型马路清扫车每天清扫6000m2 , 公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.20. 如图,在四边形ABCD中,AB=AD , CB=CD , E是CD上一点,BE交AC于F , 连接DF .
(1)、请判断直线BE与⊙A的位置关系,并说明理由;(2)、如果AB=10,BC=5,求图中阴影部分的面积.19. 某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A , B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.(1)、求这两种马路清扫车的单价;(2)、若该公司承包的道路清扫面积为118000m2 , 每辆A型马路清扫车每天清扫5000m2 , 每辆B型马路清扫车每天清扫6000m2 , 公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.20. 如图,在四边形ABCD中,AB=AD , CB=CD , E是CD上一点,BE交AC于F , 连接DF . (1)、证明:∠BAC=∠DAC , ∠AFD=∠CFE .(2)、若AB∥CD , 试证明四边形ABCD是菱形.21.
(1)、证明:∠BAC=∠DAC , ∠AFD=∠CFE .(2)、若AB∥CD , 试证明四边形ABCD是菱形.21. (1)、问题提出
(1)、问题提出如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
(2)、问题探究如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
(3)、问题解决如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD , 且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
22. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax²-2ax-3a交x轴于A、B两点,交y轴于点C , 连接BC , 且OB=OC .

 (1)、求抛物线的解析式;(2)、如图2,D为第一象限内抛物线上一点,过D做DT⊥x轴交x轴于T , 交BC于点K , 设D点横坐标为m , 线段DK的长为d , 求d与m之间的关系式;(3)、如图3,在(2)的条件下,D在对称轴右侧,Q、H为直线DT上点,Q点纵坐标为4,H在第四象限内,且QD=TH , 过D做x轴的平行线交抛物线于点E , 连接EQ交抛物线于点R , 连接RH , tan∠ERH=2,求点D的坐标.
(1)、求抛物线的解析式;(2)、如图2,D为第一象限内抛物线上一点,过D做DT⊥x轴交x轴于T , 交BC于点K , 设D点横坐标为m , 线段DK的长为d , 求d与m之间的关系式;(3)、如图3,在(2)的条件下,D在对称轴右侧,Q、H为直线DT上点,Q点纵坐标为4,H在第四象限内,且QD=TH , 过D做x轴的平行线交抛物线于点E , 连接EQ交抛物线于点R , 连接RH , tan∠ERH=2,求点D的坐标.