山东省济南市长清区2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 9的算术平方根是( )A、 B、 C、3 D、±3
-
2. 下面四个几何体中,俯视图为四边形的是( )A、
 B、
B、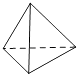 C、
C、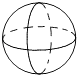 D、
D、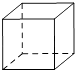
-
3. 将23000用科学记数法表示应为( )A、2.3×104 B、23×103 C、2.3×103 D、0.23×105
-
4. 如图,AB∥CD,AD和BC相交于点O,∠A=40°,∠AOB=75°.则∠C等于( )
 A、40° B、65° C、75° D、115°
A、40° B、65° C、75° D、115° -
5. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
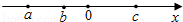 A、a﹣c>b﹣c B、a+c<b+c C、ac>bc D、
A、a﹣c>b﹣c B、a+c<b+c C、ac>bc D、 -
6. 在下列四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 .
D、
.
D、
-
7. 计算: 的正确结果是( )A、 B、1﹣x C、1 D、﹣1
-
8. 在一次爱心义卖活动中,某中学九年级6个班捐献的义卖金额(单位:元)分别为800、820、930、860、820、850,这组数据的众数和中位数分别是( )A、820,850 B、820,930 C、930,835 D、820,835
-
9. 已知 ,一次函数 与反比例函数 在同一直角坐标系中的图象可能( )A、
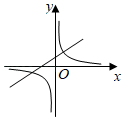 B、
B、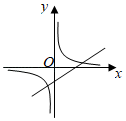 C、
C、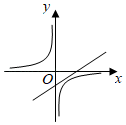 D、
D、
-
10. 如图, 内接于圆 , , ,若 ,则弧 的长为( )
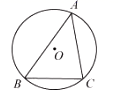 A、 B、 C、 D、
A、 B、 C、 D、 -
11. 如图,某建筑物 上挂着“巴山渝水,魅力重庆”的宣传条幅 ,王同学利用测倾器在斜坡的底部 处测得条幅底部 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡 的坡度 米, 米(点 在同平面内, ,测倾器的高度忽略不计),则条幅 的长度约为( )(参考数据: )
 A、12.5米 B、12.8米 C、13.1米 D、13.4米
A、12.5米 B、12.8米 C、13.1米 D、13.4米 -
12. 已知函数y= ,当a≤x≤b时,﹣ ≤y≤2,则b﹣a的最大值为( )A、 B、 C、 D、2
二、填空题
-
13. 分解因式:m2﹣16= .
-
14. 不透明袋子中装有6个球,其中有5个红球、1个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
-
15. 若n边形内角和为900°,则边数n= .
-
16. 代数式 与代数式 k+3的值相等时,k的值为 .
-
17. 为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程s(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第秒.

-
18. 将矩形ABCD按如图所示的方式折叠,BE,EG,FG为折痕.若顶点A,C,D都落在点O处,且点B,O,G在同一条直线上,同时点E,O,F在另一条直线上,则 的值为.

三、解答题
-
19. 计算:|﹣5|﹣20200+( )﹣2﹣2sin30°
-
20. 解不等式组 ,并写出它的最小整数解.
-
21. 如图,在矩形ABCD,AD=AE,DF⊥AE于点F.求证:AB=DF.

-
22. 为推进垃圾分类,推动绿色发展,某工厂购进甲乙两种型号的机器人用来进行垃圾分类,甲型机器人比乙型机器人每小时多分10kg , 甲型机器人分类800千克垃圾所用的时间与乙型机器人分类600kg垃圾所用的时间相等.(1)、两种机器人每小时分别分类多少垃圾?(2)、现在两种机器人共同分类500kg垃圾,工作2小时后,甲型机器人因机器维修退出,求甲型机器人退出后,乙型机器人还需工作多长时间才能完成?
-
23. 如图,BE是O的直径,点A和点D是⨀O上的两点,过点A作⊙O的切线交BE延长线于点C.
 (1)、若∠ADE=25°,求∠C的度数;(2)、若AC=4,CE=2,求⊙O半径的长.
(1)、若∠ADE=25°,求∠C的度数;(2)、若AC=4,CE=2,求⊙O半径的长. -
24. 某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的息解答下列问题:
 (1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角为度;(2)、将条形统计图补充完整;(3)、该校共有2000名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角为度;(2)、将条形统计图补充完整;(3)、该校共有2000名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率. -
25. 如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD= .
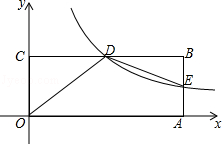 (1)、求过点D的反比例函数的解析式;(2)、求△DBE的面积;(3)、x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
(1)、求过点D的反比例函数的解析式;(2)、求△DBE的面积;(3)、x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由. -
26. 如图1,正方形ABCD和正方形AEFG,连接DG,BE.
 (1)、发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是;②直线DG与直线BE之间的位置关系是.(2)、探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.(3)、应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB= ,AE=1,则线段DG是多少?(直接写出结论)
(1)、发现:当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是;②直线DG与直线BE之间的位置关系是.(2)、探究:如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE.(3)、应用:在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB= ,AE=1,则线段DG是多少?(直接写出结论) -
27. 如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C . 直线y=x﹣5经过点B、C .
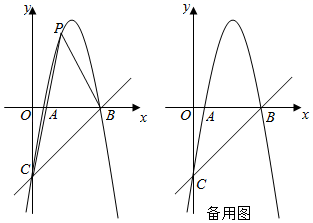 (1)、求抛物线的解析;(2)、点P是直线BC上方抛物线上一动点,连接PB、PC .
(1)、求抛物线的解析;(2)、点P是直线BC上方抛物线上一动点,连接PB、PC .①当△PBC的面积最大时,求点P的坐标;
②在①的条件下,y轴上存在点M , 使四边形PMAB的周长最小,请求出点M的坐标;
③连接AC , 当tan∠PBO=2tan∠ACO时,请直接写出点P的坐标.
