山东省济南市天桥区2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2.
有一种圆柱体茶叶筒如图所示,则它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 将4760用科学记数法表示应为( )A、47.6×102 B、4.76×103 C、4.76×104 D、0.476× 1044. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
3. 将4760用科学记数法表示应为( )A、47.6×102 B、4.76×103 C、4.76×104 D、0.476× 1044. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,AB//CD,直线EF分别交AB,CD于E,F两点,∠1=40°,则∠2等于( )
5. 如图,AB//CD,直线EF分别交AB,CD于E,F两点,∠1=40°,则∠2等于( ) A、40° B、60° C、120° D、140°6. 下列运算正确的是( )A、a2·a3=a6 B、(a+b)2=a2+b2 C、(a2)3=a6 D、a2+a3=a57. 化简: 的结果是( )A、 B、 C、 D、8. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A、40° B、60° C、120° D、140°6. 下列运算正确的是( )A、a2·a3=a6 B、(a+b)2=a2+b2 C、(a2)3=a6 D、a2+a3=a57. 化简: 的结果是( )A、 B、 C、 D、8. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )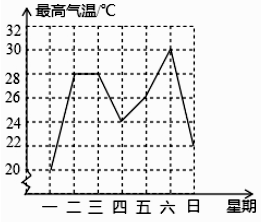 A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃9. 在同一平面直角坐标系中,函数 与 ( 为常数,且 )的图象大致( )A、
A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃9. 在同一平面直角坐标系中,函数 与 ( 为常数,且 )的图象大致( )A、 B、
B、 C、
C、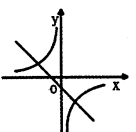 D、
D、 10. 某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
10. 某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( ) A、20 米 B、10米 C、10 米 D、20米11. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
A、20 米 B、10米 C、10 米 D、20米11. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )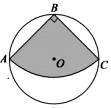 A、 B、 C、 D、12. 二次函数y=a(x-4)2-4(a≠0)的图象在2<x<3这一段位于x轴的下方,在6<x<7这一段位于x轴的上方,则a的值为( )A、1 B、-1 C、2 D、-2
A、 B、 C、 D、12. 二次函数y=a(x-4)2-4(a≠0)的图象在2<x<3这一段位于x轴的下方,在6<x<7这一段位于x轴的上方,则a的值为( )A、1 B、-1 C、2 D、-2二、填空题
-
13. 分解因式:a2+ab= .14. 一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有2个黄球和若干个白球,将口袋中的球摇匀,从中任意摸出一个球,摸到黄球的概率是 ,则白球的个数是 .15. 一个正多边形的每个外角都是36°,则它是正边形.16. 若代数式 的值是1,则 .17. 如图,已知A地在B地正南方3千米处,甲乙两人同时分别从A, B两地向正北方向匀速直行,他们与A地的距离S (千米)与所行的时间t (小时)之间的函数关系图象如图所示,当他们行走4小时后,他们之间的距离为千米.
 18. 如图,将小正方形AEFG绕大正方形ABCD的顶点A顺时针旋转一定的角度α(0°≤a≤90°),连接BG,DE相交于点O,再连接AO、BE、DG.以下四个结论:①BG=DE;②BG⊥DE;③∠DOA=∠GOA;④ .其中结论正确的是 .
18. 如图,将小正方形AEFG绕大正方形ABCD的顶点A顺时针旋转一定的角度α(0°≤a≤90°),连接BG,DE相交于点O,再连接AO、BE、DG.以下四个结论:①BG=DE;②BG⊥DE;③∠DOA=∠GOA;④ .其中结论正确的是 .
三、解答题
-
19. 计算:( )-1-(π-3.14)0-2tan45°+(-1)2020 .20. 解不等式组 ,并写出它的所有整数解.21. 如图,在菱形ABCD中,E、F分别是AD和AB的中点,连接BE、DF.求证:BE=DF.
 22. 为了调查学生对雾猫天气知识的了解程度,某校在学生中做了-次抽样调查,调查结果共分为四个等级: A.非常了解、B.比较了解、C.基本了解、D.不了解.根据调查统计结果,绘制了如图所示的不完整的两种统计图:
22. 为了调查学生对雾猫天气知识的了解程度,某校在学生中做了-次抽样调查,调查结果共分为四个等级: A.非常了解、B.比较了解、C.基本了解、D.不了解.根据调查统计结果,绘制了如图所示的不完整的两种统计图:
请结合统计图,回答下列问题:
(1)、此次参与调查的学生共有人;(2)、扇形统计图中D部分扇形所对应的圆心角是度;(3)、请补全条形统计图;(4)、根据调查结果,学校开展关于雾霾的知识竞赛,要从“非常了解”程度的4人中随机选两人参加,已知这四人中有两名男生、两名女生,请用树状图或列表法求一名男生和一名女生参加本次知识竞赛的概率.23. 如图, 的外接圆⊙O的直径为AC,P是⊙O上一点,BP平分∠ABC,连接PO、PC. (1)、求证:∠PBC=∠OPC;(2)、过点P作⊙O的切线,与BC的延长线交于点Q,若BC=2,QC=3,求PQ的长.24. 某商店欲购进A、B两种商品,已知购进A种商品5件和B种商品4件共需300元;若购进A种商品6件和B种商品8件共需440元;(1)、求A、B两种商品每件的进价分别为多少元?(2)、若该商店,A种商品每件的售价为48元,B种商品每件的售价为31元,且商店将购进A、B共50件的商品全部售出后,要获得的利润超过348元,求A种商品至少购进多少件?25. 如图1,在平面直角坐标系中,直线AB与反比例函数 的图象交于点A (1,3)和点B (3, n),与x轴交于点C,与y轴交于点D.
(1)、求证:∠PBC=∠OPC;(2)、过点P作⊙O的切线,与BC的延长线交于点Q,若BC=2,QC=3,求PQ的长.24. 某商店欲购进A、B两种商品,已知购进A种商品5件和B种商品4件共需300元;若购进A种商品6件和B种商品8件共需440元;(1)、求A、B两种商品每件的进价分别为多少元?(2)、若该商店,A种商品每件的售价为48元,B种商品每件的售价为31元,且商店将购进A、B共50件的商品全部售出后,要获得的利润超过348元,求A种商品至少购进多少件?25. 如图1,在平面直角坐标系中,直线AB与反比例函数 的图象交于点A (1,3)和点B (3, n),与x轴交于点C,与y轴交于点D.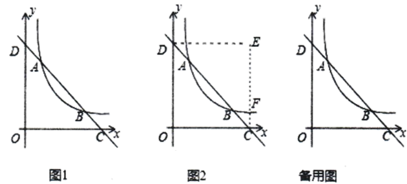 (1)、求反比例函数的表达式及n的值;(2)、将△OCD沿直线AB翻折,点O落在第一象限内的点E处, EC与反比例函数的图象交于点F.
(1)、求反比例函数的表达式及n的值;(2)、将△OCD沿直线AB翻折,点O落在第一象限内的点E处, EC与反比例函数的图象交于点F.①请求出点F的坐标;
②在x轴上是否存在点P,使得△DPF是以DF为斜边的直角三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
26. 已知 中,∠ACB=90°,点D是AB上的一点,过点A作AE⊥AB,过点C作CE⊥CD,且AE与CE相交于点E. (1)、如图1,当∠ABC=45°,试猜想CE与CD的数量关系:;(2)、如图2,当∠ABC=30°,点D在BA的延长线上,连接DE,请探究以下问题:
(1)、如图1,当∠ABC=45°,试猜想CE与CD的数量关系:;(2)、如图2,当∠ABC=30°,点D在BA的延长线上,连接DE,请探究以下问题:①CD与CE的数量关系是否发生变化?如无变化,请给予证明;如有变化,先猜想CD与CE的数量关系,再给予证明;
②若AC=2,四边形ACED的面积为3 ,试求BD的值.
27. 如图1,抛物线y=ax2+bx+c(a≠0),与x轴交于A(4,0)、O两点,点D(2,-2)为抛物线的顶点.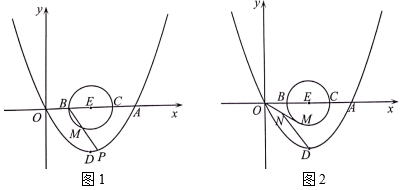 (1)、求该抛物线的解析式;(2)、点E为AO的中点,以点E为圆心、以1为半径作⊙E交x轴于B、C两点,点M为⊙E上一点.
(1)、求该抛物线的解析式;(2)、点E为AO的中点,以点E为圆心、以1为半径作⊙E交x轴于B、C两点,点M为⊙E上一点.①射线BM交抛物线于点P,设点P的横坐标为m,当tan∠MBC=2时,求m的值;
②如图2,连接OM,取OM的中点N,连接DN,则线段DN的长度是否存在最大值或最小值?若存在,请求出DN的最值;若不存在,请说明理由.