山东省济南市市中区2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
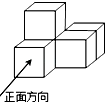
1. -2的相反数是( )A、 B、2 C、 D、2. 如图是由5个相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、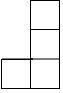 B、
B、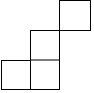 C、
C、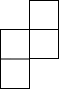 D、
D、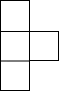 3. 自2020年1月23日起,我国仅用大概10天就建成了火神山医院,18天建成了雷神山医院,彰显了“中国速度”.雷神山医院和火神山医院总建筑面积约为113800平方米.将113800用科学记数法表示应为( )A、 B、 C、 D、4. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
3. 自2020年1月23日起,我国仅用大概10天就建成了火神山医院,18天建成了雷神山医院,彰显了“中国速度”.雷神山医院和火神山医院总建筑面积约为113800平方米.将113800用科学记数法表示应为( )A、 B、 C、 D、4. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( ) A、60° B、65° C、75° D、85°5. 下列运算正确的是( )A、 B、 C、 D、6. 江西景德镇的青花瓷是中华陶瓷工艺的珍品,下列青花瓷上的青花图案既是轴对称图形又是中心对称图形的是( )A、
A、60° B、65° C、75° D、85°5. 下列运算正确的是( )A、 B、 C、 D、6. 江西景德镇的青花瓷是中华陶瓷工艺的珍品,下列青花瓷上的青花图案既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( )
7. 如图是两个可以自由转动的转盘,其中一个转盘平均分为4份,另一个转盘平均分为3份,两个转盘分别标有数字;同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为5的概率是( ) A、 B、 C、 D、8. 化简 的结果是( )A、 B、 C、 D、9. 若关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则实数m的取值范围是( )A、m≤1 B、m≤﹣1 C、m≤1且m≠0 D、m≥1且m≠010. 某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求这棵大树AB原来的高度是( )米?(结果精确到个位,参考数据: ≈1.4, ≈1.7, ≈2.4)
A、 B、 C、 D、8. 化简 的结果是( )A、 B、 C、 D、9. 若关于x的一元二次方程mx2﹣2x+1=0有两个实数根,则实数m的取值范围是( )A、m≤1 B、m≤﹣1 C、m≤1且m≠0 D、m≥1且m≠010. 某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求这棵大树AB原来的高度是( )米?(结果精确到个位,参考数据: ≈1.4, ≈1.7, ≈2.4)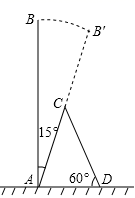 A、9 B、10 C、11 D、1211. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A、9 B、10 C、11 D、1211. 如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )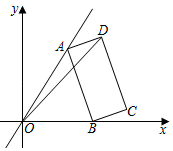 A、 B、 +2 C、 +2 D、12. 如果存在常数M , 对于任意函数值y , 满足y≤M , 那么称这个函数是有上界函数;所有满足条件M中,最小值称为这个函数的上确界.例如,函数 , ,因此有上确界是2,如果函数 上确界是n , 且函数最小值不超过2m , 则m取值范围( )A、m≤ B、m C、 D、m
A、 B、 +2 C、 +2 D、12. 如果存在常数M , 对于任意函数值y , 满足y≤M , 那么称这个函数是有上界函数;所有满足条件M中,最小值称为这个函数的上确界.例如,函数 , ,因此有上确界是2,如果函数 上确界是n , 且函数最小值不超过2m , 则m取值范围( )A、m≤ B、m C、 D、m二、填空题
-
13. 分解因式: .14. 如图是客厅里的地毯,被均匀分成16块,除颜色外其他均相同,一小狗跑来停在地毯上,它停在阴影部分的概率为 .
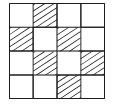 15. 方程 的解为16. 如图,在△ABC中,∠ABC=45°,∠ACB=30°,AB=2,将△ABC绕点C顺时针旋转60°得△CDE,则图中线段AB扫过的阴影部分的面积为.
15. 方程 的解为16. 如图,在△ABC中,∠ABC=45°,∠ACB=30°,AB=2,将△ABC绕点C顺时针旋转60°得△CDE,则图中线段AB扫过的阴影部分的面积为.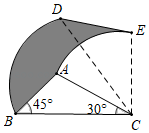 17. 张琪和爸爸到英雄山广场运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示.求张琪开始返回时与爸爸相距米.
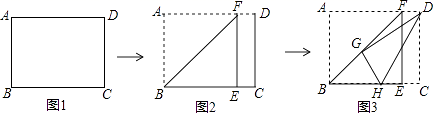
17. 张琪和爸爸到英雄山广场运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,张琪继续前行5分钟后也原路返回,两人恰好同时到家张琪和爸爸在整个运动过程中离家的路点y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示.求张琪开始返回时与爸爸相距米. 18. 如图1,有一张矩形纸片ABCD , 已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
18. 如图1,有一张矩形纸片ABCD , 已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:①AF的长为10;②△BGH的周长为18;③ = ;④GH的长为5,
其中正确的结论有 . (写出所有正确结论的序号)
三、解答题
-
19. 计算:20. 解不等式组 ,并写出它的整数解.21. 如图所示,已知平行四边形ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
 22. 某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
22. 某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题等级
A
B
C
D
频数
40
120
36
n
频率
0.2
m
0.18
0.02
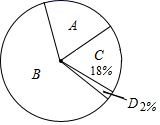 (1)、表中m= , n=;(2)、扇形统计图中,A部分所对应的扇形的圆心角是°,所抽取学生对丁雾霾了解程度的众数是;(3)、若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?23. 如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)、表中m= , n=;(2)、扇形统计图中,A部分所对应的扇形的圆心角是°,所抽取学生对丁雾霾了解程度的众数是;(3)、若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?23. 如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.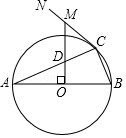 (1)、求证:MD=MC;(2)、若⊙O的半径为5,AC=4 ,求MC的长.24. 某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)、A、B型车每辆可分别载学生多少人?(2)、若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.25. 如图①,在矩形OABC中,OA=4,OC=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,连接OB , 反比例函数y= (x>0)的图象经过线段OB的中点D , 并与矩形的两边交于点E和点F , 直线l:y=kx+b经过点E和点F .
(1)、求证:MD=MC;(2)、若⊙O的半径为5,AC=4 ,求MC的长.24. 某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.(1)、A、B型车每辆可分别载学生多少人?(2)、若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.25. 如图①,在矩形OABC中,OA=4,OC=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,连接OB , 反比例函数y= (x>0)的图象经过线段OB的中点D , 并与矩形的两边交于点E和点F , 直线l:y=kx+b经过点E和点F .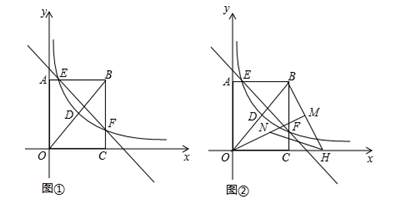 (1)、写出中点D的坐标 , 并求出反比例函数的解析式;(2)、连接OE、OF , 求△OEF的面积;(3)、如图②,将线段OB绕点O顺时针旋转一定角度,使得点B的对应点H恰好落在x轴的正半轴上,连接BH , 作OM⊥BH , 点N为线段OM上的一个动点,求HN+ ON的最小值.26. 在 中, ,将 绕点A顺时针方向旋转 角 至 的位置.(1)、如图1,当旋转角为 时,连接 与 交于点M,则 .
(1)、写出中点D的坐标 , 并求出反比例函数的解析式;(2)、连接OE、OF , 求△OEF的面积;(3)、如图②,将线段OB绕点O顺时针旋转一定角度,使得点B的对应点H恰好落在x轴的正半轴上,连接BH , 作OM⊥BH , 点N为线段OM上的一个动点,求HN+ ON的最小值.26. 在 中, ,将 绕点A顺时针方向旋转 角 至 的位置.(1)、如图1,当旋转角为 时,连接 与 交于点M,则 . (2)、如图2,在(1)条件下,连接 ,延长 交 于点D,求 的长.
(2)、如图2,在(1)条件下,连接 ,延长 交 于点D,求 的长.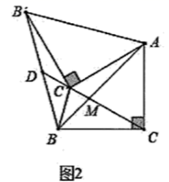 (3)、如图3,在旋转的过程中,连线 所在直线交 于点D,那么 的长有没有最大值?如果有,求出 的最大值:如果没有,请说明理由.
(3)、如图3,在旋转的过程中,连线 所在直线交 于点D,那么 的长有没有最大值?如果有,求出 的最大值:如果没有,请说明理由.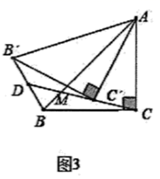 27. 如图,在平面直角坐标系 中,抛物线 与x轴相交于 两点,点C为抛物线的顶点.点 为y轴上的动点,将抛物线绕点M旋转 ,得到新的抛物线,其中 旋转后的对应点分别记为 .
27. 如图,在平面直角坐标系 中,抛物线 与x轴相交于 两点,点C为抛物线的顶点.点 为y轴上的动点,将抛物线绕点M旋转 ,得到新的抛物线,其中 旋转后的对应点分别记为 . (1)、若 ,求原抛物线的函数表达式;(2)、在(1)条件下,当四边形 的面积为 时,求m的值;(3)、探究a满足什么条件时,存在点M,使得四边形 为菱形?请说明理由.
(1)、若 ,求原抛物线的函数表达式;(2)、在(1)条件下,当四边形 的面积为 时,求m的值;(3)、探究a满足什么条件时,存在点M,使得四边形 为菱形?请说明理由.