山东省德州市武城县2020年中考数学二模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算结果正确的是（　　）

A、（﹣a³）²＝a⁹ B、a²•a³＝a⁶ C、 ${(\frac{1}{2})}^{- 1}$ ﹣2²＝﹣2 D、 ${(\cos 60^{\circ} - \frac{1}{2})}^{0}$ ＝1

查看试题解析
2. 下列图形是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 截止到 2019 年 9 月 3 日，电影《哪吒之魔童降世》的累计票房达到 47.24 亿，47.24 亿用科学记数法表示为（）

A、 $47.24 \times 10^{9}$ B、 $4.724 \times 10^{9}$ C、 $4.724 \times 10^{5}$ D、 $472.4 \times 10^{5}$

查看试题解析
4. 如图所示，将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上，若∠1=35°，则∠2的度数为（）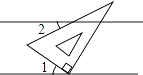

A、10° B、20° C、25° D、30°

查看试题解析
5. 我市某中学九年级（1）班为开展“阳光体育运动”，决定自筹资金为班级购买体育器材，全班50名同学捐款情况如下表：

捐款（元）

5

10

15

20

25

30

人数

3

6

11

11

13

6

问该班同学捐款金额的众数和中位数分别是（）

A、13，11 B、25，30 C、20，25 D、25，20

查看试题解析
6.
小亮领来n盒粉笔，整齐地摆在讲桌上，其三视图如图，则n的值是（　　）

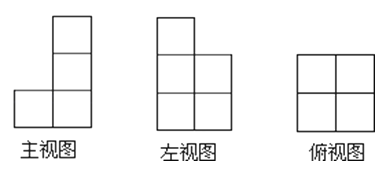A、7 B、8 C、9 D、10

查看试题解析
7. 下列说法错误的是（　　）

A、平分弦的直径，垂直于弦，并且平分弦所对的弧 B、已知⊙O的半径为6，点O到直线a的距离为5，则直线a与⊙O有两个交点 C、如果一个三角形的外心在三角形的外部，则这个三角形是钝角三角形 D、三角形的内心到三角形的三边的距离相等

查看试题解析
8. 若 $\sqrt{{(5 - x)}^{2}} = x - 5$ ，则x的取值范围是（）

A、x<5 B、x≤5 C、x≥5 D、x>5

查看试题解析
9. 九年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.设骑车学生的速度为x km/h，则所列方程正确的是（）

A、 $\frac{10}{x} = \frac{10}{2 x} - \frac{1}{3}$ B、 $\frac{10}{x} = \frac{10}{2 x} - 20$ C、 $\frac{10}{x} = \frac{10}{2 x} + \frac{1}{3}$ D、 $\frac{10}{x} = \frac{10}{2 x} + 20$

查看试题解析
10. 如图，AB为半圆的直径，其中 $A B = 4$ ，半圆绕点B顺时针旋转 $45 °$ ，点A旋转到点 $A^{'}$ 的位置，则图中阴影部分的面积为（）

A、 $π$ B、 $2 π$ C、 $\frac{π}{2}$ D、 $4 π$

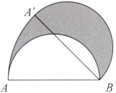查看试题解析
11. 若关于x的一元二次方程kx²﹣2x﹣1=0有两个不相等的实数根，则实数k的取值范围是（）

A、k＞﹣1 B、k＜1且k≠0 C、k≥﹣1且k≠0 D、k＞﹣1且k≠0

查看试题解析
12. 二次函数y＝ax²+bx+c（a，b，c是常数，且a≠0）中的x与y的部分对应值如表所示，则下列结论中，正确的个数有（）

x

﹣1

0

1

3

y

﹣1

3

5

3

①a＜0；②当x＜0时，y＜3；③当x＞1时，y的值随x值的增大而减小；④方程ax²+bx+c＝5有两个不相等的实数根．

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

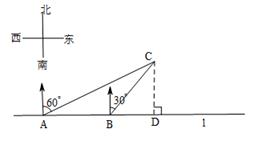
13. 分解因式：x³﹣25x＝.

查看试题解析
14. 从1、2、3中任取一个数作为十位上的数字，再从余下的数字中任取一个数作为个位上的数字，那么组成的两位数是4的倍数的概率是

查看试题解析
15. 在⊙O中，半径为2，弦AB的长为2，则弦AB所对的圆周角的度数为；

查看试题解析
16. 如图所示，在一笔直的海岸线l上有A ． B两个观测站，已知AB=2km，从A测得船C在北偏东60°的方向，从B测得船C在北偏东30°的方向，则船C离海岸线l的距离（即CD的长）为km；

查看试题解析
17. 如图，正方形ABCD的边长为1，AC、BD是对角线，将△DCB绕着点D顺时针旋转45°得到△DGH ， HG交AB于点E ，连接DE交AC于点F ，连接FG ．则下列结论：①四边形AEGF是菱形；②△HED的面积是1﹣ $\frac{\sqrt{2}}{2}$ ；③∠AFG＝135°；④BC+FG＝ $\sqrt{3}$ ．其中正确的结论是．（填入正确的序号）

查看试题解析
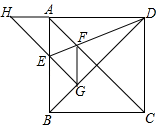18. 如图，直线l：y＝ $\frac{\sqrt{3}}{3}$ x，点A₁坐标为(0，1)，过点A₁作y轴的垂线交直线l于点B₁ ，以原点O 为圆心，OB₁长为半径画弧交y一轴于点A₂；再过点A₂作y轴的垂线交直线于点B₂ ，以原点O为圆心，OB₂长为半径画弧交y轴于点A₃ ， …，按此做法进行下去，点A₄的坐标为；点A_n的坐标为．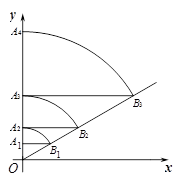

查看试题解析

三、解答题

19. 先化简，再求值： $(\frac{x^{2} - y}{x} - x - 1) \div \frac{x^{2} - y^{2}}{x^{2} - 2 x y + y^{2}}$ ，其中 $x = \sqrt{2} ， y = \sqrt{6}$ ．

查看试题解析

20.

(1)、某校招聘教师一名，现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试，他们各自的成绩如下表所示：

应聘者	专业知识	讲课	答辩
甲	70	85	80
乙	90	85	75
丙	80	90	85

按照招聘简章要求，对专业知识、讲课、答辩三项赋权5：4：1．请计算三名应聘者的平均成绩，从成绩看，应该录取谁？

(2)、我市举行了某学科实验操作考试，有A、B、C、D四个实验，规定每位学生只参加其中一个实验的考试，并由学生自己抽签决定具体的考试实验．小王，小张，小厉都参加了本次考试．

①小厉参加实验D考试的概率是　 ▲ 　；

②用列表或画树状图的方法求小王、小张抽到同一个实验的概率．

查看试题解析

21. 某出租公司有若干辆同一型号的货车对外出租，每辆货车的日租金实行淡季、旺季两种价格标准，旺季每辆货车的日租金比淡季上涨 $\frac{1}{3}$ ．据统计，淡季该公司平均每天有 $10$ 辆货车未出租，日租金总收入为 $1500$ 元；旺季所有的货车每天能全部租出，日租金总收入为 $4000$ 元．

(1)、该出租公司这批对外出租的货车共有多少辆？淡季每辆货车的日租金多少元？

(2)、经市场调查发现，在旺季如果每辆货车的日租金每上涨 $20$ 元，每天租出去的货车就会减少 $1$ 辆，不考虑其它因素，每辆货车的日租金上涨多少元时，该出租公司的日租金总收入最高？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB＝90°，点D在AB上，以AD为直径的⊙O与边BC相切于点E，与边AC相交于点G，且 $\overset{⌢}{A G}$ ＝ $\overset{⌢}{E G}$ ，连接GO并延长交⊙O于点F，连接BF.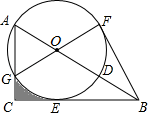

(1)、求证：①AO＝AG.②BF是⊙O的切线.

(2)、若BD＝6，求图形中阴影部分的面积.

查看试题解析
23. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图，他在山坡坡脚P处测得古塔顶端M的仰角为 $60^{°}$ ，沿山坡向上走25m到达D处，测得古塔顶端M的仰角为 $30^{°}$ .已知山坡坡度 $i = 3 ： 4$ ，即 $\tan θ = \frac{3}{4}$ ，请你帮助小明计算古塔的高度ME.（结果精确到0.1m，参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
24. 小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.

(1)、猜测探究
在 $Δ A B C$ 中， $A B = A C$ ， $M$ 是平面内任意一点，将线段 $A M$ 绕点A按顺时针方向旋转与 $∠ B A C$ 相等的角度，得到线段 $A N$ ，连接 $N B$ ．

如图1，若M是线段 $B C$ 上的任意一点，请直接写出 $∠ N A B$ 与 $∠ M A C$ 的数量关系是， $N B$ 与 $M C$ 的数量关系是；

(2)、如图2，点E是 $A B$ 延长线上点，若M是 $∠ C B E$ 内部射线 $B D$ 上任意一点，连接 $M C$ ，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．

(3)、拓展应用
如图3，在 $Δ A_{1} B_{1} C_{1}$ 中， $A_{1} B_{1} = 8$ ， $∠ A_{1} B_{1} C_{1} = 60^{\circ}$ ， $∠ B_{1} A_{1} C_{1} = 75^{\circ}$ ，P是 $B_{1} C_{1}$ 上的任意点，连接 $A_{1} P$ ，将 $A_{1} P$ 绕点 $A_{1}$ 按顺时针方向旋转 $75^{\circ}$ ，得到线段 $A_{1} Q$ ，连接 $B_{1} Q$ ．求线段 $B_{1} Q$ 长度的最小值．

查看试题解析
25. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于点 $A (- 1 ， 0)$ ，点 $B (3 ， 0)$ ，与y轴交于点C，且过点 $D (2 ， - 3)$ ．点P、Q是抛物线 $y = a x^{2} + b x + c$ 上的动点．

(1)、求抛物线的解析式；

(2)、当点P在直线OD下方时，求 $Δ P O D$ 面积的最大值．

(3)、直线OQ与线段BC相交于点E，当 $Δ O B E$ 与 $Δ A B C$ 相似时，求点Q的坐标．

查看试题解析

捐款（元）	5	10	15	20	25	30
人数	3	6	11	11	13	6

x	﹣1	0	1	3
y	﹣1	3	5	3