江西省吉安市2020年中考数学6月模拟试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 在- 、- 、-|-2|、- 这四个数中,最大的数是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为( )A、 B、 C、 D、5. 某班班长统计去年1∼8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
4. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一,它是世界总体跨度最长的跨海大桥,全长55000米.数字55000用科学记数法表示为( )A、 B、 C、 D、5. 某班班长统计去年1∼8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )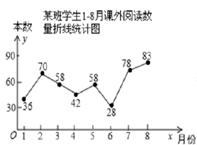 A、每月阅读数量的平均数是50 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月6. 对于抛物线 ,下列说法错误的是( )A、若顶点在x轴下方,则一元二次方程 有两个不相等的实数根 B、若抛物线经过原点,则一元二次方程 必有一根为0 C、若 ,则抛物线的对称轴必在y轴的左侧 D、若 ,则一元二次方程 ,必有一根为-2
A、每月阅读数量的平均数是50 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月6. 对于抛物线 ,下列说法错误的是( )A、若顶点在x轴下方,则一元二次方程 有两个不相等的实数根 B、若抛物线经过原点,则一元二次方程 必有一根为0 C、若 ,则抛物线的对称轴必在y轴的左侧 D、若 ,则一元二次方程 ,必有一根为-2二、填空题
-
7. 分解因式:2x2﹣8=8. 函数y= 自变量的取值范围是 .9. 已知一元二次方程 的两个实数根为 ,则( 的值是 .10. 我国古代数学名著《孙子算经》中记载了一道题,大意是: 匹马恰好拉了 片瓦,已知 匹小马能拉 片瓦, 匹大马能拉片 瓦,求小马、大马各有多少匹.若设小马有x匹,大马有y匹,依题意,可列方程组为 .11. 如图,点A是反比例函数y=的图象上的一点,过点A作AB⊥x轴,垂足为B,点C为y轴上的一点,连接AC、BC,若△ABC的面积为3,则k的值是
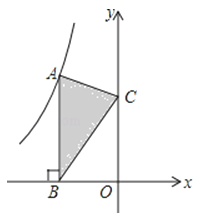 12. 如图,在矩形ABCD中,AD=2AB=2,E是BC边上的一个动点,连接AE , 过点D作DF⊥AE于F , 连接CF , 当△CDF为等腰三角形时,则BE的长是.
12. 如图,在矩形ABCD中,AD=2AB=2,E是BC边上的一个动点,连接AE , 过点D作DF⊥AE于F , 连接CF , 当△CDF为等腰三角形时,则BE的长是.
三、解答题
-
13.(1)、计算:﹣22+| ﹣4|+( )-1+2tan60°(2)、求 不 等 式 组 的解集.14. 先化简,再求值: ,其中x=﹣6.15. 如图,已知多边形ABCDEF中,AB=AF , DC=DE , BC=EF , ∠ABC=∠BCD . 请仅用无刻度的直尺,分别按下列要求画图.
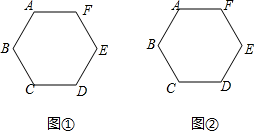 (1)、在图①中,画出一个以BC为边的矩形;(2)、在图②中,若多边形ABCDEF是正六边形,试在AF上画出点M , 使得AM= AF .16. 乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”、“T2”、“T3”、“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1、“2”、“3”、“4”的四张卡片(除数字不同外,其余均相同,数字“1”、“2”、“3”、“4”分别对应球桌号(“T1”、“T2”、“T3”、“T4”(背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛(1)、下列事件中属于必然事件的是
(1)、在图①中,画出一个以BC为边的矩形;(2)、在图②中,若多边形ABCDEF是正六边形,试在AF上画出点M , 使得AM= AF .16. 乒乓球是我国的国球,比赛采用单局11分制,是一种世界流行的球类体育项目,比赛分团体、单打、双打等数种在某站公开赛中,某直播平台同时直播4场男单四分之一比赛,四场比赛的球桌号分别为“T1”、“T2”、“T3”、“T4”(假设4场比赛同时开始),小宁和父亲准备一同观看其中的某一场比赛,但两人的意见不统一,于是采用抽签的方式决定,抽签规则如下:将正面分别写有数字“1、“2”、“3”、“4”的四张卡片(除数字不同外,其余均相同,数字“1”、“2”、“3”、“4”分别对应球桌号(“T1”、“T2”、“T3”、“T4”(背面朝上洗匀,父亲先从中随机抽取一张,小宁再从剩下的3张卡片中随机抽取一张,比较两人所抽卡片上的数字,观看较大的数字对应球桌的比赛(1)、下列事件中属于必然事件的是A . 抽到的是小宁最终想要看的一场比赛的球桌号
B . 抽到的是父亲最终想要看的一场比赛的球桌号
C . 小宁和父亲抽到同一个球桌号
D . 小宁和父亲抽到的球桌号不一样
(2)、用列表法或树状图法求小宁和父亲最终观看“T4”球桌比赛的概率17. 为鼓励市民节约用水,某市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系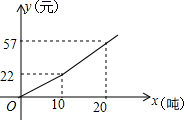 (1)、小红家五月份用水8吨,应交水费元;(2)、按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?18. 2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下
(1)、小红家五月份用水8吨,应交水费元;(2)、按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?18. 2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下成绩
3′40″及以下
3′41″-4′
4′01″-4′20″
4′21″-4′40″
4′41″及以上
等级
A
B
C
D
E
百分比
10%
25%
m
20%
n
 (1)、求样本容量及表格中的m和n的值(2)、求扇形统计图中A等级所对的圆心角度数,并补全统计图.(3)、我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?19. 如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB , AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m , BC与AN交于点M , 撑杆AN=2.2m , 固定点O到地面的距离ON=1.6m .
(1)、求样本容量及表格中的m和n的值(2)、求扇形统计图中A等级所对的圆心角度数,并补全统计图.(3)、我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?19. 如图①是钓鱼伞,为遮挡不同方向的阳光,钓鱼伞可以在撑杆AN上的点O处弯折并旋转任意角,图②是钓鱼伞直立时的示意图,当伞完全撑开时,伞骨AB , AC与水平方向的夹角∠ABC=∠ACB=30°,伞骨AB与AC水平方向的最大距离BC=2m , BC与AN交于点M , 撑杆AN=2.2m , 固定点O到地面的距离ON=1.6m . (1)、如图②,当伞完全撑开并直立时,求点B到地面的距离.(2)、某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.
(1)、如图②,当伞完全撑开并直立时,求点B到地面的距离.(2)、某日某时,为了增加遮挡斜射阳光的面积,将钓鱼伞倾斜与铅垂线HN成30°夹角,如图③.①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明: ≈1.732,结果精确到0.1m)
20. 如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E. (1)、线段AE=;(2)、如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
(1)、线段AE=;(2)、如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ▲ °时,DM与⊙O相切.
21. 绘制函数 的图象,我们经历了如下过程:确定自变量x的取值范围是x≠0; 列表﹣﹣描点﹣﹣连线,得到该函数的图象如图所示.x
…
-4
-3
-2
-1
1
2
3
4
…
y
…
2
…

观察函数图象,回答下列问题:
(1)、函数图象在第象限;(2)、函数图象的对称性是A . 既是轴对称图形,又是中心对称图形 B . 只是轴对称图形,不是中心对称图形
C . 不是轴对称图形,而是中心对称图形 D . 既不是轴对称图形,也不是中心对称图形
(3)、在x>0时,当x=时,函数y有最(大,小)值,且这个最值等于;在x<0时,当x=时,函数y有最(大,小)值,且这个最值等于;
(4)、方程 是否有实数解?说明理由.22. 定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在 与 中, ,且 所以称 与 为“关联等腰三角形”,设它们的顶角为 ,连接 ,则称 会为“关联比".下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
(1)、当 与 为“关联等腰三角形”,且 时,①在图1中,若点E落在 上,则“关联比” = ▲
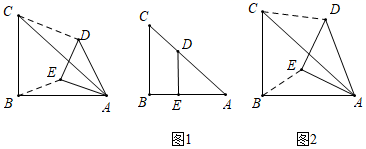
②在图2中,探究 与 的关系,并求出“关联比” 的值.
 (2)、[类比探究]
(2)、[类比探究]如图3,
①当 与 为“关联等腰三角形”,且 时,“关联比” =
②猜想:当 与 为“关联等腰三角形”,且 时,“关联比” = (直接写出结果,用含 的式子表示)
(3)、[迁移运用]如图4, 与 为“关联等腰三角形”.若 点 为 边上一点,且 ,点E为 上一动点,求点E自点B运动至点P时,点D所经过的路径长.
23. 如图,已知二次函数L1:y=mx2+2mx﹣3m+1(m≥1)和二次函数L2:y=﹣m(x﹣3)2+4m﹣1(m≥1)图象的顶点分别为M,N,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边).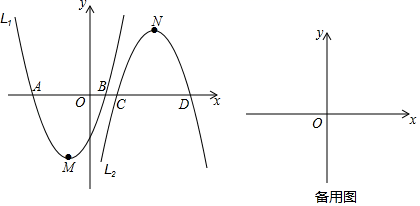 (1)、函数y=mx2+2mx﹣3m+1(m≥1)的顶点坐标为;当二次函数L1 , L2的y值同时随着x的增大而增大时,则x的取值范围是;(2)、当AD=MN时,判断四边形AMDN的形状(直接写出,不必证明);(3)、抛物线L1 , L2均会分别经过某些定点,
(1)、函数y=mx2+2mx﹣3m+1(m≥1)的顶点坐标为;当二次函数L1 , L2的y值同时随着x的增大而增大时,则x的取值范围是;(2)、当AD=MN时,判断四边形AMDN的形状(直接写出,不必证明);(3)、抛物线L1 , L2均会分别经过某些定点,①求所有定点的坐标;
②若抛物线L1位置固定不变,通过左右平移抛物线L2的位置使这些定点组成的图形为菱形,则抛物线L2应平移的距离是多少?