青海省西宁市2020年中考数学一模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

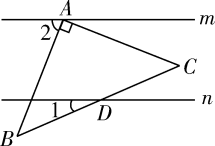
1. 下列各数中，最大的数是（）

A、 $\frac{1}{4}$ B、0 C、 $- \frac{1}{2}$ D、-2

查看试题解析
2. 下列各数中，是无理数的是（）

A、3.1415 B、 $\sqrt{4}$ C、 $\frac{22}{7}$ D、 $\sqrt{6}$

查看试题解析
3. 下列运算正确的是（）

A、 ${(- 2 a)}^{2} = - 4 a^{2}$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(a^{5})}^{2} = a^{7}$ D、 $(- a + 2) (- a - 2) = a^{2} - 4$

查看试题解析
4. 已知直线m∥n，将一块含45°角的直角三角板ABC按如图方式放置，其中斜边BC与直线n交于点D.若∠1=25°，则∠2的度数为（）

A、60° B、65° C、70° D、75°

查看试题解析
5. 在2019年的体育中考中，某校6名学生的体育成绩统计如图所示，则这组数据的众数，中位数依次是（）

A、50，48 B、48，49 C、48，48 D、50，49

查看试题解析
6. 如图， $⊙ O$ 的直径 $A B$ 垂直于弦 $C D$ ，垂足是点 $E$ ， $∠ C A O = 22.5 °$ ， $O C = 8$ ，则弦 $C D$ 的长为（）

A、 $8 \sqrt{2}$ B、 $4 \sqrt{2}$ C、 $8 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 如图，在 $R t Δ A B C$ 中， $∠ B = 90^{\circ}$ ，以点 $A$ 为圆心，适当长为半径画弧，分别交 $A B 、 A C$ 于点 $D ， E$ ，再分别以点 $D 、 E$ 为圆心，大于 $\frac{1}{2} D E$ 为半径画弧，两弧交于点 $F$ ，作射线 $A F$ 交边 $B C$ 于点 $B G = 1 ， A C = 4$ ，则 $Δ A C G$ 的面积是（）

A、 $1$ B、 $\frac{3}{2}$ C、 $2$ D、 $\frac{5}{2}$

查看试题解析
8. 如图是抛物线 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 图象的一部分，抛物线的顶点是 $A$ ，对称轴是直线 $x = 1$ ，且抛物线与 $x$ 轴的一个交点为 $B (4 ， 0)$ ；直线 $A B$ 的解析式为 $y_{2} = m x + n (m \neq 0)$ ．下列结论：① $2 a + b = 0$ ；② $a b c > 0$ ；③方程 $a x^{2} + b x + c = m x + n$ 有两个不相等的实数根；④抛物线与 $x$ 轴的另一个交点是 $(- 1 ， 0)$ ；⑤当 $1 < x < 4$ 时，则 $y_{1} > y_{2}$ ．其中正确的是（）

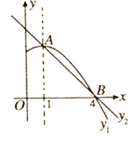A、①② B、①③⑤ C、①④ D、①④⑤

查看试题解析

二、填空题

9. 近年来，中国高铁发展迅速，高铁技术不断走出国门，成为展示我国实力的新名片，现在中国高速铁路营运里程将达到23000公里，将23000用科学记数法表示应为．

查看试题解析
10. 函数y＝ $\frac{1}{2 x + 1}$ 中，自变量x的取值范围是．

查看试题解析
11. 分解因式：3a³﹣6a²+3a＝．

查看试题解析
12. 已知一个多边形的内角和为540°，则这个多边形是边形．

查看试题解析
13. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是方程组 ${\begin{array}{l} a x + b y = 2 \\ b x + a y = - 3 \end{array}$ 的解，则 $a + b$ 的值是

查看试题解析
14. 如图，正方形二维码的边长为2cm，为了测算图中黑色部分的面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.7左右，据此可估计黑色部分的面积约为cm² ．

查看试题解析
15. 一个圆锥的底面半径 $r = 4$ ，高 $h = 3$ ，则这个圆锥的侧面积是（结果取整数）．

查看试题解析
16. 如图，将等腰直角三角形ABC（∠B=90°）沿EF折叠，使点A落在BC边的中点A₁处，BC=8，那么线段AE的长度为．

查看试题解析
17. 已知 $△ A B C$ 中， $A B = 10$ ， $A C = 2 \sqrt{7}$ ， $∠ B = 30^{°}$ ，则 $B C$ 的长等于

查看试题解析
18. 如图，点 $P$ 是双曲线 $C$ ： $y = \frac{4}{x}$ （ $x > 0$ ）上的一点，过点 $P$ 作 $x$ 轴的垂线交直线 $A B$ ： $y = \frac{1}{2} x - 2$ 于点 $Q$ ，连结 $O P$ ， $O Q$ .当点 $P$ 在曲线 $C$ 上运动，且点 $P$ 在 $Q$ 的上方时，△ $P O Q$ 面积的最大值是.

查看试题解析

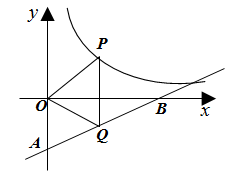
三、解答题

19. 解不等式组： ${\begin{array}{l} - 3 x - 1 \leq 2 \\ 2 (x + 2) < x + 5 \end{array}$

查看试题解析
20. 解方程： $\frac{3 x}{x - 1} - \frac{2}{1 - x} = 1$

查看试题解析
21. 计算： $| \sqrt{3} - 1 | - 4 \sin 60^{°} + {(\frac{1}{6})}^{- 1}$

查看试题解析
22. 先化简，再求值： $\frac{b}{a^{2} - b^{2}} \div (\frac{a}{a - b} - 1)$ ，其中 $a, b$ 满足 ${(a - \sqrt{3})}^{2} + \sqrt{b + 1} = 0$

查看试题解析
23. 如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为（4，6）．反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过BC的中点D，与AB交于点E，连接DE．

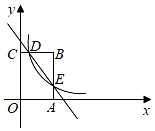(1)、求k的值；

(2)、求直线DE的解析式．

查看试题解析
24. 如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.

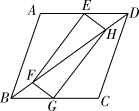(1)、求证：BG=DE；

(2)、若E为AD中点，FH=2，求菱形ABCD的周长。

查看试题解析
25. 如今很多初中生喜欢购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：A：白开水，B：瓶装矿泉水，C：碳酸饮料，D：非碳酸饮料，根据统计结果绘制如下两个不完整的统计图，根据统计图提供的信息，解答下列问题：

(1)、这个班级有名同学；并补全条形统计图；

(2)、若该班同学每人每天只饮用一种饮品（每种仅限一瓶，价格如表），则该班同学每天用于饮品的人均花费是多少元？

(3)、在饮用白开水的同学中有4名班委干部，为了养成良好的生活习惯，班主任决定在这4名班委干部（其中有两位班长记为A，B，其余两位记为C，D）中随机抽取2名作为良好习惯监督员，请用列表法或画树状图的方法，求出恰好抽到2名班长的概率．

查看试题解析
26. 如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD，CD，过点D作PD∥BC与AB的延长线相交于点P．

(1)、求证：PD是⊙O的切线；

(2)、求证：BD²＝PB•AC．

查看试题解析
27. 某水果店购进一批优质晚熟芒果，进价为10元/千克，售价不低于15元/千克，且不超过40元/千克，根据销售情况发现该芒果在一天内的销售量y（千克）与该天的售价x（元/千克）之间满足如表所示的一次函数关系：

(1)、写出销售量y与售价x之间的函数关系式；

(2)、设某天销售这种芒果获利W元，写出W与售价x之间的函数关系式，并求出当售价为多少元时，当天的获利最大，最大利润是多少？

查看试题解析
28. 如图，在平面直角坐标系xOy中，已知抛物线的顶点为A（2， $\frac{9}{2}$ ），抛线物与y轴交于点B（0， $\frac{5}{2}$ ），点C在其对称轴上且位于点A下方，将线段AC绕点C按顺时针方向旋转90°，点A落在抛物线上的点P处．

(1)、求抛物线的解析式；

(2)、求线段AC的长；

(3)、将抛物线平移，使其顶点A移到原点O的位置，这时点P落在点D的位置，如果点M在y轴上，且以O，C，D，M为顶点的四边形的面积为8，求点M的坐标．

查看试题解析