内蒙古兴安盟乌兰浩特市2020年中考数学二模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数0，2， $\sqrt{5}$ ，3中，最大的是（）

A、0 B、2 C、 $\sqrt{5}$ D、3

查看试题解析
2. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列调查中，适合采用全面调查（普查）方式的是（）

A、对綦江河水质情况的调查 B、对端午节期间市场上粽子质量情况的调查 C、对某班50名同学体重情况的调查 D、对某类烟花爆竹燃放安全情况的调查

查看试题解析
4. 计算（a³）²•a³的结果是（）

A、a⁸ B、a⁹ C、a¹⁰ D、a¹¹

查看试题解析
5. 测试五位学生的“一分钟跳绳”成绩，得到五个各不相同的数据，在统计时，出现了一处错误：将最高成绩写得更高了，计算结果不受影响的是（）

A、方差 B、标准差 C、中位数 D、平均数

查看试题解析
6. 若关于x的方程 ${kx}^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则k的取值范围是 $($ 　　 $)$

A、 $k > - 1$ B、 $k < - 1$ C、 $k \geq - 1$ 且 $k \neq 0$ D、 $k > - 1$ 且 $k \neq 0$

查看试题解析
7. 直角三角板和直尺如图放置，若∠1=20°，则∠2的度数为（）

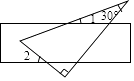A、60° B、50° C、40° D、30°

查看试题解析
8. 下列命题中的真命题是（）
①相等的角是对顶角 ②矩形的对角线互相平分且相等 ③垂直于半径的直线是圆的切线 ④顺次连接四边形各边中点所得四边形是平行四边形．

A、①② B、②③ C、③④ D、②④

查看试题解析
9. 某校学生小明每天骑自行车上学时都要经过一个十字路口，设十字路口有红、黄、绿三色交通信号灯，他在路口遇到红灯的概率为 $\frac{1}{3}$ ，遇到黄灯的概率为 $\frac{1}{9}$ ，那么他遇到绿灯的概率为（　　）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看试题解析
10. 如图，在正方形ABCD中，AB=3，点M在CD的边上，且DM=1，ΔAEM与ΔADM关于AM所在的直线对称，将ΔADM按顺时针方向绕点A旋转90°得到ΔABF，连接EF，则线段EF的长为（）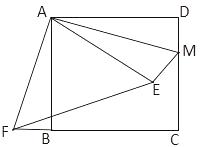

A、3 B、 $2 \sqrt{3}$ C、 $\sqrt{13}$ D、 $\sqrt{15}$

查看试题解析
11. 如图，在菱形ABCD中，AC=6 $\sqrt{2}$ ，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（）

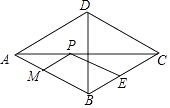A、6 B、3 $\sqrt{3}$ C、2 $\sqrt{6}$ D、4.5

查看试题解析
12. 如图是二次函数y=ax²+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）

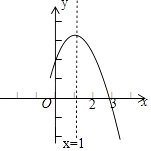A、①②④ B、①②⑤ C、②③④ D、③④⑤

查看试题解析

二、填空题

13. 地球的体积约为10¹²立方千米，太阳的体积约为1.4×10¹⁸立方千米，地球的体积约是太阳体积的倍数是（用科学记数法表示，保留2位有效数字）

查看试题解析
14. 分解因式：9ax²﹣ay²＝．

查看试题解析
15. 使得代数式 $\frac{1}{\sqrt{x - 3}}$ 有意义的 $x$ 的取值范围是．

查看试题解析
16. 等腰三角形 $A B C$ 中，顶角 $A$ 为 $40^{\circ}$ ，点 $P$ 在以 $A$ 为圆心， $B C$ 长为半径的圆上，且 $B P = B A$ ，则 $∠ P B C$ 的度数为．

查看试题解析
17. 如图，四边形OABC是平行四边形，点C在x轴上，反比例函数y= $\frac{k}{x}$ （x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为．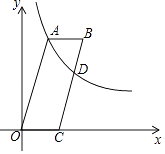

查看试题解析

三、解答题

18. 计算：|﹣4|+3tan60°﹣ $\sqrt{12}$ ﹣（ $\frac{1}{2}$ ）^﹣¹

查看试题解析
19. 先化简，再求值．
$\frac{1}{1 - x} \div \frac{x^{2} + 2 x}{x^{2} - 2 x + 1} + \frac{1}{x + 2}$ ，请从不等式组 ${\begin{array}{l} 5 - 2 x ⩾ 1 \\ x + 3 > 0 \end{array}$ 的整数解中选择一个你喜欢的求值．

查看试题解析
20. 如图，已知以△ABC的三边为边在BC的同侧作等边△ABD、△BCE、△ACF，请回答下列问题：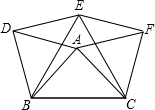

(1)、四边形ADEF是什么四边形？写出理由。

(2)、当△ABC满足什么条件时，四边形ADEF是菱形？

查看试题解析
21. 美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图，测得∠DAC=45°，∠DBC=65°．若AB=132米，求观景亭D到南滨河路AC的距离约为多少米？（结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）

查看试题解析
22. 某校利用暑假进行田径场的改造维修，项目承包单位派遣一号施工队进场施工，计划用40天时间完成整个工程：当一号施工队工作5天后，承包单位接到通知，有一大型活动要在该田径场举行，要求比原计划提前14天完成整个工程，于是承包单位派遣二号与一号施工队共同完成剩余工程，结果按通知要求如期完成整个工程.

(1)、若二号施工队单独施工，完成整个工程需要多少天？

(2)、若此项工程一号、二号施工队同时进场施工，完成整个工程需要多少天？

查看试题解析
23. 如图，点O是△ABC的边AB上一点，⊙O与边AC相切于点E，与边BC，AB分别相交于点D，F，且DE=EF．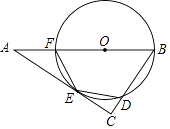

(1)、求证：∠C=90°；

(2)、当BC=3，sinA= $\frac{3}{5}$ 时，求AF的长．

查看试题解析
24. “校园诗歌大赛”结束后，张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理，并分别绘制成扇形统计图和频数直方图部分信息如下：

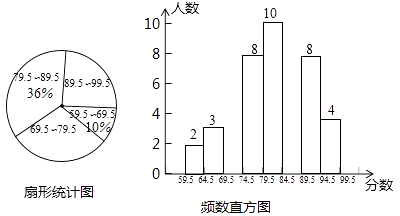(1)、本次比赛参赛选手共有人，扇形统计图中“69.5～79.5”这一组人数占总参赛人数的百分比为；

(2)、赛前规定，成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分，试判断他能否获奖，并说明理由；

(3)、成绩前四名是2名男生和2名女生，若从他们中任选2人作为获奖代表发言，试求恰好选中1男1女的概率.

查看试题解析
25. 某商场销售一种进价为每件10元的日用商品，经调查发现，该商品每天的销售量 $y$ （件）与销售单价 $x$ （元）满足 $y = - 10 x + 400$ ，设销售这种商品每天的利润为 $W$ （元）.

(1)、求 $W$ 与 $x$ 之间的函数关系式；

(2)、在保证销售量尽可能大的前提下，该商场每天还想获得2000元的利润，应将销售单价定为多少元？

(3)、当每天销售量不少于50件，且销售单价至少为32元时，该商场每天获得的最大利润是多少？

查看试题解析
26. 如图，抛物线y=﹣x²+bx+c与x轴分别交于点A、B，与y轴交于点C，且OA=1，OB=3，顶点为D，对称轴交x轴于点Q．

(1)、求抛物线对应的二次函数的表达式；

(2)、点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标；

(3)、在抛物线的对称轴上是否存在一点M，使得△DCM∽△BQC？如果存在，求出点M的坐标；如果不存在，请说明理由．

查看试题解析