内蒙古呼和浩特市回民区2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 某种食品保存的温度是-2±2℃,以下几个温度中,适合储存这种食品的是( )A、1℃ B、-8℃ C、4℃ D、-1℃2. 下列艺术字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数y=ax+b的图象大致是( )
3. 已知函数y=(x﹣a)(x﹣b)(其中a>b)的图象如图所示,则函数y=ax+b的图象大致是( ) A、
A、 B、
B、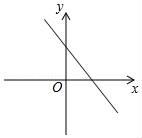 C、
C、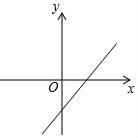 D、
D、 4. 某射击运动员在训练中射击了10次,成绩如图所示,下列结论错误的是( )
4. 某射击运动员在训练中射击了10次,成绩如图所示,下列结论错误的是( )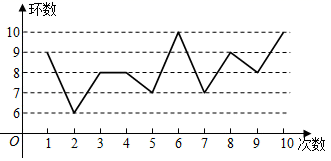 A、众数是8 B、中位数是8 C、平均数是8 D、极差是45. 如果不等式 的解集是 ,则不等式 的解集是( ).A、 B、 C、 D、6. 如图,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( )
A、众数是8 B、中位数是8 C、平均数是8 D、极差是45. 如果不等式 的解集是 ,则不等式 的解集是( ).A、 B、 C、 D、6. 如图,一个几何体的三视图分别是两个矩形,一个扇形,则这个几何体表面积的大小为( ) A、12π B、15π C、12π+6 D、15π+127. 若a2+1=5a,b2+1=5b,且a≠b,则a+b的值为( )A、﹣1 B、1 C、﹣5 D、58. 如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
A、12π B、15π C、12π+6 D、15π+127. 若a2+1=5a,b2+1=5b,且a≠b,则a+b的值为( )A、﹣1 B、1 C、﹣5 D、58. 如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )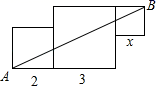 A、1或4 B、2或3 C、3或4 D、1或29. 现有A、B两枚均匀的骰子(骰子的每个面上分别标有数字1,2,3,4,5,6).以小莉掷出A骰子正面朝上的数字为x、小明掷出B骰子正面朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P在已知抛物线y=﹣x2+5x上的概率为( )A、 B、 C、 D、10. 已知抛物线y=ax2+bx+c(a>0)交x轴于点A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m,n)(n<0)在该抛物线上.下列四个判断:①b2﹣4ac≥0;②若a+c=b+3,则该抛物线一定经过点(1,3);③方程ax2+bx+c=n的解是x=m;④当m= 时,△PAB的面积最大.其中判断一定正确的序号是( )A、① B、② C、③ D、④
A、1或4 B、2或3 C、3或4 D、1或29. 现有A、B两枚均匀的骰子(骰子的每个面上分别标有数字1,2,3,4,5,6).以小莉掷出A骰子正面朝上的数字为x、小明掷出B骰子正面朝上的数字为y来确定点P(x,y),那么它们各掷一次所确定的点P在已知抛物线y=﹣x2+5x上的概率为( )A、 B、 C、 D、10. 已知抛物线y=ax2+bx+c(a>0)交x轴于点A(x1 , 0),B(x2 , 0),且x1<x2 , 点P(m,n)(n<0)在该抛物线上.下列四个判断:①b2﹣4ac≥0;②若a+c=b+3,则该抛物线一定经过点(1,3);③方程ax2+bx+c=n的解是x=m;④当m= 时,△PAB的面积最大.其中判断一定正确的序号是( )A、① B、② C、③ D、④二、填空题
-
11. 因式分解:x3y2﹣x3=.12. 根据如下程序,解决下列问题:
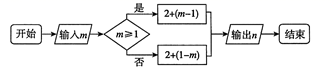 (1)、当m=-1时,n=;(2)、若n=6,则m= .13. 如图,直线y=﹣x+5与双曲线y= (x>0)相交于A,B两点, 与x轴相交于C点,△BOC的面积是 ,若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= (x>0)的交点坐标为 .
(1)、当m=-1时,n=;(2)、若n=6,则m= .13. 如图,直线y=﹣x+5与双曲线y= (x>0)相交于A,B两点, 与x轴相交于C点,△BOC的面积是 ,若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= (x>0)的交点坐标为 . 14. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球,且摸到红球的概率为 ,那么口袋中其余球的个数为个.15. 如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,△AEG的面积为4,则四边形BEGF的面积为 .
14. 在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有4个红球,且摸到红球的概率为 ,那么口袋中其余球的个数为个.15. 如图,在正方形ABCD中,点E在AB边上,且AE:EB=2:1,AF⊥DE于G交BC于F,△AEG的面积为4,则四边形BEGF的面积为 .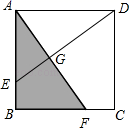 16. x , y为实数,且满足 ,则y的最大值是 .
16. x , y为实数,且满足 ,则y的最大值是 .三、解答题
-
17. 计算(1)、(2)、先化简,再求值: ,其中ab满足18. 证明“角的内部到角的两边的距离相等的点在角的平分线上”.19. 已知方程组 中x为负数,y为非正数.(1)、求a的取值范围;(2)、在a的取值范围中,当a为何整数时,不等式 的解集为20. 钓鱼岛自古就是中国的领土,我国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.M、N为钓鱼岛上东西海岸线上的两点,MN之间的距离约为3km,某日,我国一艘海监船从A点沿正北方向巡航,在A点测得岛屿的西端点N在点A的北偏东35°方向;海监船继续航行4km后到达B点,测得岛屿的东端点M在点B的北偏东59°方向,求N点距离海监船航线的最短距离(结果用含非特殊角的三角函数表示即可).
 21. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
21. 某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:学生/成绩/次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
169
165
168
169
172
173
169
167
乙
161
174
172
162
163
172
172
176
两名同学的8次跳高成绩数据分析如下表:
学生/成绩/名称
平均数
(单位:cm)
中位数
(单位:cm)
众数
(单位:cm)
方差
(单位:cm2)
甲
a
b
c
d
乙
169
172
172
31.25
根据图表信息回答下列问题:
(1)、求出a、b、c、d的值(2)、这两名同学中,的成绩更为稳定;(填甲或乙)(3)、若预测跳高165cm就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择哪位同学参赛,并说明理由;22. 某公司需要粉刷一些相同的房间,经调查3名师傅一天粉刷8个房间,还剩40m2刷不完;5名徒弟一天可以粉刷9个房间;每名师傅比徒弟一天多刷30m2的墙面。(1)、求每个房间需要粉刷的面积;(2)、该公司现有36个这样的房间需要粉刷,若只聘请1名师傅和2名徒弟一起粉刷,需要几天完成?(3)、若来该公司应聘的有3名师傅和10名徒弟,每名师傅和每名徒弟每天的工资分别是240元和200元,该公司要求这36个房间要在2天内粉刷完成,问人工费最低是多少?23. 如图,AB是⊙O的直径,C点在⊙O上,AD平分角∠BAC交⊙O于D,过D作直线AC的垂线,交AC的延长线于E,连接BD,CD. (1)、求证:BD=CD;(2)、求证:直线DE是⊙O的切线;(3)、若DE= ,AB=4,求AD的长.24. 如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方的曲线记作M,将该抛物线位于x轴下方的部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC,BC.
(1)、求证:BD=CD;(2)、求证:直线DE是⊙O的切线;(3)、若DE= ,AB=4,求AD的长.24. 如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方的曲线记作M,将该抛物线位于x轴下方的部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC,BC. (1)、求曲线N所在抛物线的函数表达式;(2)、求△ABC外接圆的面积;(3)、点P为曲线M或曲线N上的动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标;
(1)、求曲线N所在抛物线的函数表达式;(2)、求△ABC外接圆的面积;(3)、点P为曲线M或曲线N上的动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标;