内蒙古鄂尔多斯市东胜区2020年中考数学一模试卷

试卷更新日期：2021-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上A点表示的数的倒数是（）

A、 $- \frac{1}{3}$ B、3 C、﹣3 D、 $\frac{1}{3}$

查看试题解析
2. 2019年“十一”黄金周期间，鄂尔多斯市接待旅游总人数为167.5万人次．其中167.5万用科学记数法表示为（）

A、167.5×10⁴ B、16.75×10⁵ C、1.675×10⁶ D、1.675×10⁷

查看试题解析
3. 下列计算正确的是（）

A、 $2 x y - x y = 1$ B、 ${(- 3 x - 2 y)}^{2} = 9 x^{2} - 12 x y + 4 y^{2}$ C、 ${({xy}^{2})}^{3} = {xy}^{6}$ D、3x²÷4x＝ $\frac{3}{4}$ x

查看试题解析
4. 钉钉打卡已经成为一种工作方式，老师利用钉钉调查了全班学生平均每天的阅读时间，统计结果如下表，在本次调查中，全班学生平均每天阅读时间的中位数和众数分别是（）

平均每天阅读时间（小时）

0.5

1

1.5

2

人数

8

9

10

3

A、2，1.5 B、1，1.5 C、1，2 D、1，1

查看试题解析
5. 东胜到呼市相距234千米，采用“和谐”号动车组提速后，列车行驶速度是原来速度的2.2倍．从东胜到呼市的时间缩短了1.2小时．设列车提速后所需时间为 $x$ 小时，根据题意，可列方程（）

A、 $\frac{234}{x} - \frac{234}{2.2 x} = 1.2$ B、 $\frac{234}{x + 1.2} = \frac{234}{x} \times 2.2$ C、 $\frac{234}{2.2 x} - \frac{234}{x} = 1.2$ D、 $\frac{234}{x + 1.2} \times 2.2 = \frac{234}{x}$

查看试题解析
6. 如图，已知菱形ABCD的顶点B（-3，0），C（2，0），点A在y轴的正半轴上．按以下步骤作图：①以点B为圆心，适当长度为半径作弧，分别交边AB、BC于点M、N；②分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径作弧，两弧在∠ABC内交于点P；③作射线BP，交菱形的对角线AC于点E，则点E的坐标为（）

A、（1， $\frac{5}{2}$ ） B、（1，2） C、（ $\frac{\sqrt{5}}{2}$ ，2） D、（ $\frac{\sqrt{5}}{2}$ ， $\frac{5}{2}$ ）

查看试题解析
7. 如图是一个由若干个小正方体组成的几何体的主视图和左视图，则组成该几何体的小正方体个数最少是（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
8. 如图，在圆⊙O内有折线OABC，其中OA＝4，BC＝10，∠A＝∠B＝60°，则AB的长为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图，正方形ABCB₁中，AB＝1，AB与直线m的夹角为30°，延长CB₁交直线m于点A₁ ，作正方形A₁B₁C₁B₂ ，延长C₁B₂交直线m于点A₂ ，作正方形A₂B₂C₂B₃ ，延长C₂B₃交直线m于点A₃ ，作正方形A₃B₃C₃B₄ ， …，依此规律，则A₂₀₂₀A₂₀₂₁等于（）

A、 $2 \times 3^{2020}$ B、 $2 \times {(\sqrt{3})}^{2021}$ C、 $2 \times 3^{1010}$ D、 $2 \times {(\sqrt{3})}^{1010}$

查看试题解析
10. 已知二次函数y＝﹣x²+x+6及一次函数y＝x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝x+m与这个新图象有四个交点时，m的取值范围是（）

A、﹣7＜m＜﹣3 B、3＜m＜6 C、﹣7＜m＜3 D、﹣3＜m＜6

查看试题解析

二、填空题

11. 函数 $y = \frac{1}{\sqrt{3 - 2 x}}$ 中自变量x的取值范围是．

查看试题解析
12. 如图，一把直尺的边缘AB经过一块三角板DCB的直角顶点B，交斜边CD于点A，直尺的边缘EF分别交CD，BD于点E，F，若∠D=60°，∠ABC=20°，则∠1的度数为．

查看试题解析
13. 桌子上有6杯同样型号的杯子，其中1杯84消毒液，2杯75%的酒精，3杯双氧水，从6个杯子中随机取出1杯，请你将下列事件发生的可能性从大到小排列：．（填序号即可）①取到75%的酒精；②取到双氧水；③没有取到75%的酒精；④取到84消毒液．

查看试题解析
14. 下列命题中，是真命题的是．
① $\sqrt{81}$ 的平方根是 $\pm 3$ ；②有一个角是70^o的两个等腰三角形相似；③定理的逆命题是真命题；④ $\frac{22}{7} ， π ， 3.14144 ， \sqrt{12} ， \sqrt[3]{27}$ 有4个无理数；⑤垂直于弦的直径一定平分弦所对的弧．

查看试题解析
15. 已知：甲、乙两车分别从相距300km的A，B两地同时出发相向而行，甲到B地后立即返回，如图是它们离各自出发地的距离y与行驶时间x之间的函数图象．根据图像求甲乙两车在行驶过程中相遇的时间是小时．

查看试题解析
16. 阅读材料：在平面直角坐标系xOy中，点P（x₀ ， y₀）到直线Ax+By+C=0的距离公式为：d= $\frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ．例如：求点P₀（0，0）到直线4x+3y﹣3=0的距离．
解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，∴点P₀（0，0）到直线4x+3y﹣3=0的距离为d= $\frac{| 4 \times 0 + 3 \times 0 - 3 |}{\sqrt{4^{2} + 3^{2}}} = \frac{3}{5}$ ．根据以上材料，解决下列问题：如图，已知：⊙C是以点C（2，1）为圆心，1为半径的圆，设点P为⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=4，则S_△ABP的最大值．

查看试题解析

三、解答题

17.

(1)、解不等式组： ${\begin{array}{l} \frac{1 - 2 x}{3} - \frac{4 - 3 x}{6} \geq \frac{x - 2}{2} \\ 2 x - 7 < 3 (x - 1) \end{array}$ ，并求出其整数解的和；

(2)、先化简，再求值： $(\frac{a^{2} - 4}{a^{2} - 4 a + 4} - \frac{1}{2 - a}) \div \frac{a + 3}{a^{3} - 2 a^{2}}$ ，其中 $a = | \sqrt{3} - 2 | + {(π - 3.14)}^{0} + \tan 60^{o}$ ．

查看试题解析
18. 为推进社会主义新农村建设，东胜区某社区决定组建社区文体团队，现围绕“你最喜欢的文体活动项目（每人仅限一项）”，在全社区范围内随机抽取部分居民进行问卷调查，并将调查结果绘制如下两幅不完整的统计图．请你根据统计图解答下列问题：

(1)、扇形统计图中“纸牌”所在扇形的圆心角的度数为；并补全条形统计图；

(2)、若在“纸牌、象棋、跳棋、军棋”这四个项目中任选两项组队参加元旦节庆典活动，请用列表法或画树状图的方法，求恰好选中“象棋、军棋”这两个项目的概率．

查看试题解析
19. 图1是小明在健身器材上进行仰卧起坐锻炼时情景．图2是小明锻炼时上半身由EM位置运动到与地面垂直的EN位置时的示意图．已知BC＝0.64米，AD＝0.24米，α＝18°．（sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）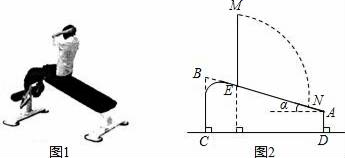

(1)、求AB的长（精确到0.01米）；

(2)、若测得EN＝0.8米，试计算小明头顶由M点运动到N点的路径弧MN的长度（结果保留π）

查看试题解析
20. 如图，已知直线AB： $y= \sqrt{3} x + 2 \sqrt{3}$ 与反比例函数 $y= \frac{3 \sqrt{3}}{x}$ 的图象交于C和D两点．

(1)、求∠ACO的度数；

(2)、将△OBC绕点O顺时针旋转α度（0°＜α＜90°），得到△OB₁C₁ ，当α为多少度时OC₁⊥AB，并求此时线段AB₁的长．

查看试题解析
21. 如图，AB是半圆O的直径，点P是半圆上不与点A，B重合的动点，PC∥AB，点M是OP中点．

(1)、求证：四边形OBCP是平行四边形；

(2)、填空：
①当∠BOP=时，四边形AOCP是菱形；

②当∠ABP=时，PC是⊙O的切线．

③若AB=2，当AP=时，四边形OBCP是正方形．

查看试题解析
22. 空气净化器越来越被人们认可，某商场购进A、B两种型号的空气净化器，如果销售5台A型和10台B型空气净化器的销售总价为20000元，销售10台A型和5台B型空气净化器的销售总价为17500元．

(1)、求每台A型空气净化器和B型空气净化器的销售单价；

(2)、该商场计划一次购进两种型号的空气净化器共100台，其中B型空气净化器的进货量不超过A型空气净化器的2倍，设购进A型空气净化器m台，这100台空气净化器的销售总价为y元．
①求y关于m的函数关系式；

②当销售总价最大时，该公司购进A型、B型空气净化器各多少台？

(3)、在（2）的条件下，若A型空气净化器每台的进价为800元，B型空气净化器每台的进价z（元）满足z=-10m+700的关系式，则销售完这批空气净化器能获取的最大利润是多少元？

查看试题解析
23. 如图，直线 $y = - x + 3$ 与x轴、y轴分别相交于点B、C，经过B、C两点的抛物线 $y = a x^{2} - 4 x + c$ 与x轴的另一个交点为A，顶点为P．

(1)、求该抛物线的解析式；

(2)、点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由；

(3)、点E为抛物线在第四象限内一点，连接BE，将直线BC向下平移经过点P，与BE交于点F，连接CE、CF，求△CEF的面积的最大值，及其对应的点E的坐标．

查看试题解析
24. 定义：如图1，点M、N把线段AB分割成AM、MN和BN，若以AM、MN、BN为边的三角形是一个直角三角形，则称点M、N是线段AB的勾股点．

(1)、已知点M、N是线段AB的勾股点，若AM＝1，MN＝2，则BN＝．

(2)、（类比探究）如图2，DE是△ABC的中位线，M、N是AB边的勾股点（AM＜MN＜NB），连接 CM、CN分别交DE于点G、H．求证：G、H是线段DE的勾股点．

(3)、（知识迁移）如图3，C，D是线段AB的勾股点，以CD为直径画⊙O，P在⊙O上，AC＝CP，连结PA，PB，若∠A＝2∠B，求∠B的度数．

(4)、（拓展应用）如图4，点P（a，b）是反比例函数 $y =$ $\frac{2}{x}$ （x＞0）上的动点，直线 $y = - x + 2$ 与坐标轴分别交于A、B两点，过点P分别向x、y轴作垂线，垂足为C、D，且交线段AB于E、F．证明：E、F是线段AB的勾股点．

查看试题解析

平均每天阅读时间（小时）	0.5	1	1.5	2
人数	8	9	10	3