内蒙古包头市青山区2020年中考数学二模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法正确的是( )A、“打开电视机,正在播世界杯足球赛”是必然事件 B、“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就有1次正面朝上 C、一组数据2,3,4,5,5,6的众数和中位数都是5 D、甲组数据的方差S甲2=0.24,乙组数据的方差S甲2=0.03,则乙组数据比甲组数据稳定3. 如图为某同学网上答题的结果,他做对的题数是( )
2. 下列说法正确的是( )A、“打开电视机,正在播世界杯足球赛”是必然事件 B、“掷一枚硬币正面朝上的概率是”表示每抛掷硬币2次就有1次正面朝上 C、一组数据2,3,4,5,5,6的众数和中位数都是5 D、甲组数据的方差S甲2=0.24,乙组数据的方差S甲2=0.03,则乙组数据比甲组数据稳定3. 如图为某同学网上答题的结果,他做对的题数是( )① ② ③ ④ ⑤科学记数法表示
A、2个 B、3个 C、4个 D、5个4. 如图,M、N、P、Q是数轴上的四个点,这四个点中最适合表示 ﹣1的点是( )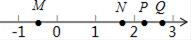 A、点M B、点N C、点P D、点Q5. 如果 ,那么代数式 的值为( )A、 B、 C、 D、6. 如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A、点M B、点N C、点P D、点Q5. 如果 ,那么代数式 的值为( )A、 B、 C、 D、6. 如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )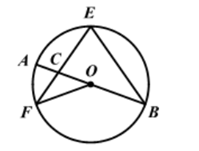 A、20° B、35° C、40° D、55°7. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )A、360元 B、720元 C、1080元 D、2160元8. 直线y=kx沿y轴向下平移4个单位长度后与x轴的交点坐标是(-3,0),以下各点在直线y=kx上的是( )A、(-4,0) B、(0,3) C、(3,-4) D、(-4,3)9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.
A、20° B、35° C、40° D、55°7. 制作一块3m×2m长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是( )A、360元 B、720元 C、1080元 D、2160元8. 直线y=kx沿y轴向下平移4个单位长度后与x轴的交点坐标是(-3,0),以下各点在直线y=kx上的是( )A、(-4,0) B、(0,3) C、(3,-4) D、(-4,3)9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是( )
 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 关于x的一元二次方程x2+2x+k+1=0的两个实根x1 , x2 , 满足x1+x2﹣x1x2<﹣1,则k的取值范围在数轴上表示为( )A、
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 关于x的一元二次方程x2+2x+k+1=0的两个实根x1 , x2 , 满足x1+x2﹣x1x2<﹣1,则k的取值范围在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 11. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )
11. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )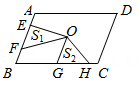 A、 B、 C、 D、12. 某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用5元.为尽快回笼资金,该电商计划开展降价促销活动.通过市场调研发现,该时装售价每降价1元,每天销量增加4件.若该电商每天扣除平台推广费之后的利润要达到4500元,则适合的售价应定于( )A、70元 B、80元 C、70元或90元 D、90元
A、 B、 C、 D、12. 某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用5元.为尽快回笼资金,该电商计划开展降价促销活动.通过市场调研发现,该时装售价每降价1元,每天销量增加4件.若该电商每天扣除平台推广费之后的利润要达到4500元,则适合的售价应定于( )A、70元 B、80元 C、70元或90元 D、90元二、填空题
-
13. 计算: .14. 若一个多边形的内角和与外角和之和是900°,则该多边形的边数是 .15. 某班有50名学生,平均身高为166cm,其中20名女生的平均身高为163cm,则30名男生的平均身高为cm.16. 如图,在扇形OAB中,∠AOB=100°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在 上的点D处,折痕交OA于点C,则 的长为 .
 17. 如图,一艘船由A港沿北偏东 方向航行 至B港,然后再沿北偏西 方向航行至C港,C港在A港北偏东 方向,则A,C两港之间的距离为 .
17. 如图,一艘船由A港沿北偏东 方向航行 至B港,然后再沿北偏西 方向航行至C港,C港在A港北偏东 方向,则A,C两港之间的距离为 . 18. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?“其意思为:速度快的人走100步,速度慢的人只走60步,现速度慢的人先走100步,速度快的人去追赶,则速度快的人要走步才能追到速度慢的人.19.
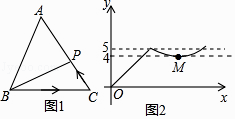
18. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之?“其意思为:速度快的人走100步,速度慢的人只走60步,现速度慢的人先走100步,速度快的人去追赶,则速度快的人要走步才能追到速度慢的人.19.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是 .
 20. ▱ABCD中,对角线AC、BD相交于点O , E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F , 连接AF , CE , 下列四个结论中:
20. ▱ABCD中,对角线AC、BD相交于点O , E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F , 连接AF , CE , 下列四个结论中:①对于动点E , 四边形AECF始终是平行四边形;
②若∠ABC<90°,则至少存在一个点E , 使得四边形AECF是矩形;
③若AB>AD , 则至少存在一个点E , 使得四边形AECF是菱形;
④若∠BAC=45°,则至少存在一个点E , 使得四边形AECF是正方形.
以上所有正确说法的序号是 .
三、解答题
-
21. 2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).
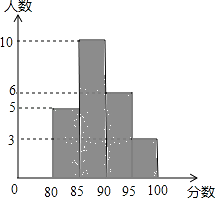 (1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.22. 如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.22. 如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.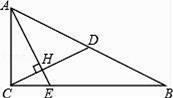 (1)、求sinB的值;(2)、如果CD= ,求BE的值.23. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点.
(1)、求sinB的值;(2)、如果CD= ,求BE的值.23. 如图,一次函数y=kx+b与反比例函数 的图象交于A(m,6),B(3,n)两点. (1)、求一次函数的解析式;(2)、根据图象直接写出 的x的取值范围;(3)、求△AOB的面积.24. 如图, 为⊙ 的直径, , 为圆上的两点, ,弦 , 相交于点 ,
(1)、求一次函数的解析式;(2)、根据图象直接写出 的x的取值范围;(3)、求△AOB的面积.24. 如图, 为⊙ 的直径, , 为圆上的两点, ,弦 , 相交于点 ,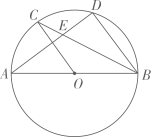 (1)、求证:(2)、若 , ,求⊙ 的半径;(3)、在(2)的条件下,过点 作⊙ 的切线,交 的延长线于点 ,过点 作 交⊙ 于 , 两点(点 在线段 上),求 的长.25. 问题:如图1,在 中, ,点 是射线 上任意一点, 是等边三角形,且点 在 的内部,连接 .探究线段 与 之间的数量关系.
(1)、求证:(2)、若 , ,求⊙ 的半径;(3)、在(2)的条件下,过点 作⊙ 的切线,交 的延长线于点 ,过点 作 交⊙ 于 , 两点(点 在线段 上),求 的长.25. 问题:如图1,在 中, ,点 是射线 上任意一点, 是等边三角形,且点 在 的内部,连接 .探究线段 与 之间的数量关系.
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
(1)、当点 与点 重合时(如图2),请你补全图形.由 的度数为 , 点 落在 , 容易得出 与 之间的数量关系为 (2)、当 是 的平分线时,判断 与 之间的数量关系并证明(3)、当点 在如图3的位置时,请你画出图形,研究 三点是否在以 为圆心的同一个圆上,写出你的猜想并加以证明.
(2)、当 是 的平分线时,判断 与 之间的数量关系并证明(3)、当点 在如图3的位置时,请你画出图形,研究 三点是否在以 为圆心的同一个圆上,写出你的猜想并加以证明. 26. 在平面直角坐标系 中,已知抛物线 与 轴交于点 和点 (点 在点 的左侧),与 轴交于点 ,对称轴是直线 .
26. 在平面直角坐标系 中,已知抛物线 与 轴交于点 和点 (点 在点 的左侧),与 轴交于点 ,对称轴是直线 . (1)、求抛物线的表达式;(2)、直线 平行于 轴,与抛物线交于 、 两点(点 在点 的左侧),且 ,点 关于直线 的对称点为 ,求线段 的长;(3)、点 是该抛物线上一点,且在第一象限内,联结 、 , 交线段 于点 ,当 时,求点 的坐标.
(1)、求抛物线的表达式;(2)、直线 平行于 轴,与抛物线交于 、 两点(点 在点 的左侧),且 ,点 关于直线 的对称点为 ,求线段 的长;(3)、点 是该抛物线上一点,且在第一象限内,联结 、 , 交线段 于点 ,当 时,求点 的坐标.