内蒙古包头市北重一中2020年中考数学三模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
1. 若 ,则 ( )A、12 B、4 C、32 D、22. 如图,是一种氮气弹簧零件的实物图,可以近似看成两个圆柱对接而成,其左视图是( )
 A、
A、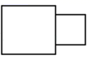 B、
B、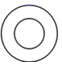 C、
C、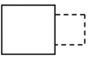 D、
D、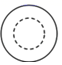 3. 下列计算正确的是( )A、2a+3b=5ab B、(a-b)2=a2-b2 C、(2x2)3=6x6 D、x8÷x3=x54. 下列命题正确的是( )A、概率是1%的事件在一次试验中一定不会发生 B、要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式 C、甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定 D、随意翻到一本书的某页,页码是奇数是随机事件5.
3. 下列计算正确的是( )A、2a+3b=5ab B、(a-b)2=a2-b2 C、(2x2)3=6x6 D、x8÷x3=x54. 下列命题正确的是( )A、概率是1%的事件在一次试验中一定不会发生 B、要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式 C、甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定 D、随意翻到一本书的某页,页码是奇数是随机事件5.如图是按 的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
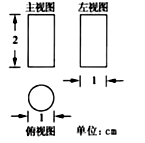 A、 B、 C、 D、6. 估计 的值在( )A、3和3.5之间 B、2.5和3之间 C、2和2.5之间 D、1.5和2之间7. 已知:如图, , 分别是半圆 和半圆 的直径,半圆 的弦 交半圆 于 .若 ,则 等于( )
A、 B、 C、 D、6. 估计 的值在( )A、3和3.5之间 B、2.5和3之间 C、2和2.5之间 D、1.5和2之间7. 已知:如图, , 分别是半圆 和半圆 的直径,半圆 的弦 交半圆 于 .若 ,则 等于( )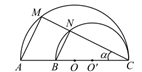 A、 B、 C、 D、8. 小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法错误的是( )
A、 B、 C、 D、8. 小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法错误的是( ) A、∠A=60° B、△ACD是直角三角形 C、BC= CD D、点B是△ACD的外心9. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )
A、∠A=60° B、△ACD是直角三角形 C、BC= CD D、点B是△ACD的外心9. 如右图,矩形EFGH内接于△ABC,且边FG落在BC上,如果AD⊥BC,BC=3,AD=2,EF:EH=2:3,那么EH的长为( )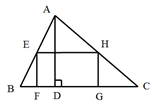 A、 B、 C、 D、210. 已知关于x的一元二次方程 有两个不相等的实数根,m为整数且 ,若t是满足该条件时方程的一个根,则代数式 的值为( )A、 B、 C、 D、711. 已知下列命题:①若 ,则 ;②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧;③对角线互相平分且相等的四边形是菱形,④如果两条弧相等,那么它们所对的圆心角相等;⑤在函数 中,自变量x的取值范围是 且 ;⑥若 则 ,其中正确命题的个数是( )A、4个 B、3个 C、2个 D、1个12. 如图, ,射线 和 互相垂直,点 是 上的一个动点,点 在射线 上, ,作 并截取 ,连结 并延长交射线 于点 .设 ,则 关于 的函数解析式是( )
A、 B、 C、 D、210. 已知关于x的一元二次方程 有两个不相等的实数根,m为整数且 ,若t是满足该条件时方程的一个根,则代数式 的值为( )A、 B、 C、 D、711. 已知下列命题:①若 ,则 ;②平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧;③对角线互相平分且相等的四边形是菱形,④如果两条弧相等,那么它们所对的圆心角相等;⑤在函数 中,自变量x的取值范围是 且 ;⑥若 则 ,其中正确命题的个数是( )A、4个 B、3个 C、2个 D、1个12. 如图, ,射线 和 互相垂直,点 是 上的一个动点,点 在射线 上, ,作 并截取 ,连结 并延长交射线 于点 .设 ,则 关于 的函数解析式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算: .14. 响应党中央号召,连日来,全国广大共产党员继续踊跃捐款,表达对新冠肺炎疫情防控工作的支持.据统计,截至3月10日,全国已有7436万多名党员自愿捐款,共捐款76.8亿元,则76.8亿元用科学记数法可表示为元.15. 化简求值: .(其中x满足 ).16. 如图,在一笔直的海岸线1上有相距 的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线1的距离是 .
 17. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为 . (答案用根号表示)
17. 如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为 . (答案用根号表示)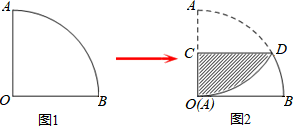 18. 某商店经销一种销售成本为每千克40元的水产品,规定试销期间销售单价不低于成本价.据试销发现,月销售量y(千克)与销售单价x(元)符合一次函数 .在使顾客获得实惠的条件下,要使月销售利润达到8000元,销售单价应定为元.19. 若关于x的方程 + =3的解为正数,则m的取值范围是.20. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
18. 某商店经销一种销售成本为每千克40元的水产品,规定试销期间销售单价不低于成本价.据试销发现,月销售量y(千克)与销售单价x(元)符合一次函数 .在使顾客获得实惠的条件下,要使月销售利润达到8000元,销售单价应定为元.19. 若关于x的方程 + =3的解为正数,则m的取值范围是.20. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
三、解答题
-
21. “只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):

血型统计表
血型
A
B
AB
O
人数
10
5
(1)、本次随机抽取献血者人数为人,图中m=;(2)、补全表中的数据;(3)、若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?(4)、现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.22. 如图,在四边形 中, . (1)、求 的值;(2)、若 ,求 的长.23. 如图,一次函数y=kx+b(k<0)的图象与反比例函数y= 图象都经过点A(a,4),一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
(1)、求 的值;(2)、若 ,求 的长.23. 如图,一次函数y=kx+b(k<0)的图象与反比例函数y= 图象都经过点A(a,4),一次函数y=kx+b(k<0)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3. (1)、求这两个函数的表达式;(2)、将直线AB向下平移5个单位长度后与第四象限内的反比例函数图象交于点D,连接AD、BD,求△ADB的面积.24. 如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连结AD并延长,与过C点的直线交于P , OD与BC相交于点E .
(1)、求这两个函数的表达式;(2)、将直线AB向下平移5个单位长度后与第四象限内的反比例函数图象交于点D,连接AD、BD,求△ADB的面积.24. 如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连结AD并延长,与过C点的直线交于P , OD与BC相交于点E .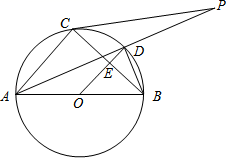 (1)、求证:OE= AC;(2)、连接CD , 若∠PCD=∠PAC , 试判断直线PC与⊙O的位置关系,并说明理由.(3)、在(2)的条件下,当AC=6,AB=10时,求切线PC的长.25. 如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与点C和点 重合),连接PB,过点P作 交射线DA于点F,连接BF. 已知AD=3 ,CD=3,设CP的长为x,
(1)、求证:OE= AC;(2)、连接CD , 若∠PCD=∠PAC , 试判断直线PC与⊙O的位置关系,并说明理由.(3)、在(2)的条件下,当AC=6,AB=10时,求切线PC的长.25. 如图,四边形ABCD是矩形,点P是对角线AC上一动点(不与点C和点 重合),连接PB,过点P作 交射线DA于点F,连接BF. 已知AD=3 ,CD=3,设CP的长为x,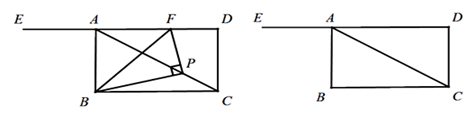 (1)、线段 的最小值 , 当x=1时, ;(2)、如图,当动点 运动到AC的中点时, 与 的交点为G, 的中点为 ,求线段GH的长度;(3)、当点 在运动的过程中,
(1)、线段 的最小值 , 当x=1时, ;(2)、如图,当动点 运动到AC的中点时, 与 的交点为G, 的中点为 ,求线段GH的长度;(3)、当点 在运动的过程中,①试探究 是否会发生变化?若不改变,请求出 大小;若改变,请说明理由;
②当 为何值时, 是等腰三角形?
26. 已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.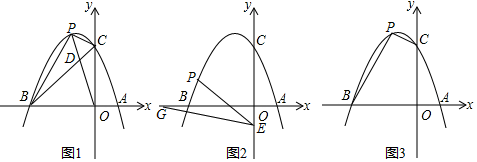 (1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;(3)、如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;(4)、如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、抛物线的解析式为 , 抛物线的顶点坐标为;(2)、如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;(3)、如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;(4)、如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.