辽宁省葫芦岛市绥中县2020年中考数学一模试卷
试卷更新日期:2021-03-25 类型:中考模拟
一、单选题
-
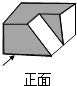
1. 若实数 的绝对值是4,则实数 等于( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图所示的工件的主视图是( )
 A、
A、 B、
B、 C、
C、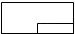 D、
D、 4.
4.下列美丽的图案中,既是轴对称图形又是中心对称图形的个数有( )
 A、1个 B、2个 C、3个 D、4个5. 某青年排球队12名队员年龄情况如下:
A、1个 B、2个 C、3个 D、4个5. 某青年排球队12名队员年龄情况如下:年龄
18
19
20
21
22
人数
1
4
3
2
2
则这12名队员年龄的众数、中位数分别是( )
A、20,19 B、19,19 C、19,20.5 D、19,206. 若关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是( )A、 且 B、 C、 且 D、7. 将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( ) A、45° B、50° C、60° D、75°8. 如图,有一张直角三角形的纸片,两直角边 , ,现将直角边 沿直线 折叠,使它落在斜边 上且与 重合,则 的长为( )
A、45° B、50° C、60° D、75°8. 如图,有一张直角三角形的纸片,两直角边 , ,现将直角边 沿直线 折叠,使它落在斜边 上且与 重合,则 的长为( ) A、 B、 C、 D、9. 如图,点 在双曲线 上,点 在双曲线 上, 轴,过点 作 轴于 .连接 ,与 相交于点 ,若 ,则 的值为( )
A、 B、 C、 D、9. 如图,点 在双曲线 上,点 在双曲线 上, 轴,过点 作 轴于 .连接 ,与 相交于点 ,若 ,则 的值为( ) A、6 B、9 C、10 D、1210. 开口向下,对称轴为直线x=-1的抛物线y=ax2+bx+c与x轴的一个交点的横坐标是x0 , 且满足0<x0<1,有下列结论:
A、6 B、9 C、10 D、1210. 开口向下,对称轴为直线x=-1的抛物线y=ax2+bx+c与x轴的一个交点的横坐标是x0 , 且满足0<x0<1,有下列结论:①abc<0;②4a-2b+c>0;③ax2-bx≤a-b;④3b+2c<0.其中,正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 据雾霾天气影响着我国北方中东部地区,给人们的健康带来严重的危害.为了让人们对雾霾有所了解.摄影师张超通过显微镜,将空气中细小的霾颗粒放大1000倍,发现这些霾颗粒平均直径为10微米~20微米,其中20微米(1米 微米)用科学记数法可表示为米.12. 因式分解: .13. 在函数y=中,自变量x的取值范围是 .
14. 桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,现在从桶里随机摸出一个球,则摸到白球的概率为 .15. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 .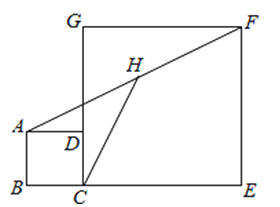 16. 如图,点A ,B,C,D分别是圆O上四点,∠ABD=20°, BD是直径,那么∠ACB = .
16. 如图,点A ,B,C,D分别是圆O上四点,∠ABD=20°, BD是直径,那么∠ACB = . 17. 如图所示,直线 经过正方形 的顶点 ,分别过顶点 、 作 于点 、 于点 ,若 , ,则 的长为 .
17. 如图所示,直线 经过正方形 的顶点 ,分别过顶点 、 作 于点 、 于点 ,若 , ,则 的长为 . 18. 正方形 、 、 …按如图放置,其中点 、 、 …在 轴正半轴上,点 、 、 …在直线 上,依此类推,点 的坐标是 .
18. 正方形 、 、 …按如图放置,其中点 、 、 …在 轴正半轴上,点 、 、 …在直线 上,依此类推,点 的坐标是 .
三、解答题
-
19. 先化简,再求值:( ) ,其中a= ﹣1.20. 随着社会经济的发展,汽车逐渐走入平常百姓家.某数学兴趣小组随机抽取了我市某单位部分职工进行调查,对职工购车情况分4类(A:车价40万元以上;B:车价在20—40万元;C:车价在20万元以下;D:暂时未购车)进行了统计,并将统计结果绘制成以下条形统计图和扇形统计图.请结合图中信息解答下列问题:
 (1)、调查样本人数为 , 样本中B类人数百分比是 , 其所在扇形统计图中的圆心角度数是;(2)、把条形统计图补充完整;(3)、该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.21. 如图,已知 三个顶点的坐标是 , , .
(1)、调查样本人数为 , 样本中B类人数百分比是 , 其所在扇形统计图中的圆心角度数是;(2)、把条形统计图补充完整;(3)、该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.21. 如图,已知 三个顶点的坐标是 , , . (1)、将 绕原点 顺时针旋转 得 ,画出 ,并写出 、 、 的坐标;(2)、 和 关于原点 对称,画出 ;(3)、以点 为位似中心,将 缩小为原来的 ,请直接写出点 的对应点 的坐标.22. 如图, 是 的直径, 与 相切于点 ,过 作 交 于点 ,过 作 于点 ,交 的延长线于点 ,连接 .
(1)、将 绕原点 顺时针旋转 得 ,画出 ,并写出 、 、 的坐标;(2)、 和 关于原点 对称,画出 ;(3)、以点 为位似中心,将 缩小为原来的 ,请直接写出点 的对应点 的坐标.22. 如图, 是 的直径, 与 相切于点 ,过 作 交 于点 ,过 作 于点 ,交 的延长线于点 ,连接 . (1)、求证: 是 的切线;(2)、若直径 的长为12, ,求 的值.23. 小明要测量公园里被湖水隔开的两个凉亭 和 之间的距离,他在 处测得凉亭 在 的北偏东 方向,他从 处沿南偏东 走了100米到达 处,测得凉亭 在 的北偏东 方向.
(1)、求证: 是 的切线;(2)、若直径 的长为12, ,求 的值.23. 小明要测量公园里被湖水隔开的两个凉亭 和 之间的距离,他在 处测得凉亭 在 的北偏东 方向,他从 处沿南偏东 走了100米到达 处,测得凉亭 在 的北偏东 方向. (1)、求 的度数;(2)、求两个凉亭 , 之间的距离.(结果精确到1米)
(1)、求 的度数;(2)、求两个凉亭 , 之间的距离.(结果精确到1米)(参考数据: , , )
24. 辽西某镇是著名的“葡萄之乡”,有大规模的葡萄批发市场.又到了葡萄成熟的季节,为了增加农民的收入,当地政府组织专家组进行了市场调查.调查人员发现葡萄每天的销售量 (吨)是销售单价 (千元)的一次函数,如图所示;另外,葡萄的种植包装成本4(千元/吨),为了保障农民的收益,今年的销售单价不能低于去年葡萄的销售单价10(千元/吨),每天的最低销售量不能低于30吨. (1)、求销售量 (吨)与销售单价 (千元)之间的函数关系式.并写出自变量 的取值范围.(2)、求出销售利润 (千元)与销售单价 (千元)之间的函数关系式,并求出当 为多少时,销售利润最大,并求出最大值.25. 已知: 是等腰直角三角形,点 在斜边 所在的直线上,连接 ,以 为腰作等腰直角三角形 ,将线段 绕点 顺时针旋转 ,得到线段 ,连接 , , , .
(1)、求销售量 (吨)与销售单价 (千元)之间的函数关系式.并写出自变量 的取值范围.(2)、求出销售利润 (千元)与销售单价 (千元)之间的函数关系式,并求出当 为多少时,销售利润最大,并求出最大值.25. 已知: 是等腰直角三角形,点 在斜边 所在的直线上,连接 ,以 为腰作等腰直角三角形 ,将线段 绕点 顺时针旋转 ,得到线段 ,连接 , , , . (1)、如图①,当点 在线段 上时,求证: ;(2)、如图②,当点 在线段 延长线上时,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出正确的结论,并说明理由;(3)、当点 在线段 延长线上时,试判断四边形 的形状,并说明理由.26. 如图,二次函数 的图象与 轴交于 , ,与 轴交于点 .
(1)、如图①,当点 在线段 上时,求证: ;(2)、如图②,当点 在线段 延长线上时,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请写出正确的结论,并说明理由;(3)、当点 在线段 延长线上时,试判断四边形 的形状,并说明理由.26. 如图,二次函数 的图象与 轴交于 , ,与 轴交于点 . (1)、求该二次函数的解析式及点 的坐标;(2)、如图1,点 为抛物线 段一动点, 于点 , 轴交 于点 ,当 的长度最大时,求点 的坐标.(3)、点 为抛物线上一点,过 作 轴交直线 于点 ,点 为 轴上一点,点 为坐标系内一点,当以点 , , , 为顶点的四边形是正方形时,直接写出点 的坐标.
(1)、求该二次函数的解析式及点 的坐标;(2)、如图1,点 为抛物线 段一动点, 于点 , 轴交 于点 ,当 的长度最大时,求点 的坐标.(3)、点 为抛物线上一点,过 作 轴交直线 于点 ,点 为 轴上一点,点 为坐标系内一点,当以点 , , , 为顶点的四边形是正方形时,直接写出点 的坐标.