2015年福建省漳州市平和五中高考数学模拟试卷（理科）

试卷更新日期：2016-07-22 类型：高考模拟

进入出卷网下载

一、单选题

1. 复数z=（3﹣2i）i的共轭复数 $\bar{z}$ 等于（　　）

A、﹣2﹣3i B、﹣2+3i C、2﹣3i D、2+3i

查看试题解析
2. 某空间几何体的正视图是三角形，则该几何体不可能是（　　）

A、圆柱 B、圆锥 C、四面体 D、三棱柱

查看试题解析
3. 等差数列{a_n}的前n项和为S_n ，若a₁=2，S₃=12，则a₆等于（　　）

A、8 B、10 C、12 D、14

查看试题解析
4.
若函数y=log_ax（a＞0，且a≠1）的图象如图所示，则下列函数图象正确的是（　　）

A、 B、 C、 D、

查看试题解析
5. 阅读如图所示的程序框图，运行相应的程序，输出的S的值等于（）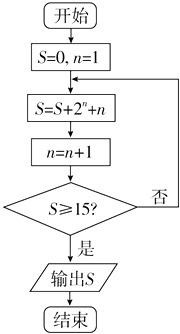

A、18 B、20 C、21 D、40

查看试题解析
6. 直线l：y=kx+1与圆O：x²+y²=1相交于A，B 两点，则“k=1”是“△OAB的面积为 $\frac{1}{2}$ ”的（　　）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分又不必要条件

查看试题解析
7. 已知函数f（x）= $\{\begin{matrix} x^{2} + 1 (x > 0) \\ \cos x (x \leq 0) \end{matrix}$ ，则下列结论正确的是（　　）

A、f（x）是偶函数 B、f（x）在R上是增函数 C、f（x）是周期函数 D、f（x）的值域为[﹣1，+∞）

查看试题解析
8. 在下列向量组中，可以把向量 $\vec{a}$ =（3，2）表示出来的是（　　）

A、 $\vec{e_{1}}$ =（0，0）， $\vec{e_{2}}$ =（1，2） B、 $\vec{e_{1}}$ =（﹣1，2）， $\vec{e_{2}}$ =（5，﹣2） C、 $\vec{e_{1}}$ =（3，5）， $\vec{e_{2}}$ =（6，10） D、 $\vec{e_{1}}$ =（2，﹣3）， $\vec{e_{2}}$ =（﹣2，3）

查看试题解析
9. 设P，Q分别为圆x²+（y﹣6）²=2和椭圆 $\frac{x^{2}}{10}$ +y²=1上的点，则P，Q两点间的最大距离是（　　）

A、5 $\sqrt{2}$ B、 $\sqrt{46}$ + $\sqrt{2}$ C、7+ $\sqrt{2}$ D、6 $\sqrt{2}$

查看试题解析
10. 用a代表红球，b代表蓝球，c代表黑球，由加法原理及乘法原理，从1个红球和1个蓝球中取出若干个球的所有取法可由（1+a）（1+b）的展开式1+a+b+ab表示出来，如：“1”表示一个球都不取、“a”表示取出一个红球，而“ab”则表示把红球和蓝球都取出来．以此类推，下列各式中，其展开式可用来表示从5个无区别的红球、5个无区别的蓝球、5个有区别的黑球中取出若干个球，且所有的蓝球都取出或都不取出的所有取法的是（　　）

A、（1+a+a²+a³+a⁴+a⁵）（1+b⁵）（1+c）⁵ B、（1+a⁵）（1+b+b²+b³+b⁴+b⁵）（1+c）⁵ C、（1+a）⁵（1+b+b²+b³+b⁴+b⁵）（1+c⁵） D、（1+a⁵）（1+b）⁵（1+c+c²+c³+c⁴+c⁵）

查看试题解析

二、填空题

11. 若变量 x，y满足约束条件 $\{\begin{matrix} x - y + 1 \leq 0 \\ x + 2 y - 8 \leq 0 \\ x \geq 0 \end{matrix}$ ，则z=3x+y的最小值为

查看试题解析
12. 在△ABC中，A=60°，AC=2，BC= $\sqrt{3}$ ，则AB等于

查看试题解析
13. 要制作一个容器为4m³ ，高为1m的无盖长方形容器，已知该容器的底面造价是每平方米20元，侧面造价是每平方米10元，则该容器的最低总造价是（单位：元）

查看试题解析
14.
如图，在边长为e（e为自然对数的底数）的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为

查看试题解析
15. 若集合{a，b，c，d}={1，2，3，4}，且下列四个关系：
①a=1；②b≠1；③c=2；④d≠4有且只有一个是正确的，则符合条件的有序数组（a，b，c，d）的个数是

查看试题解析

三、解答题

16. 已知函数f（x）=cosx（sinx+cosx）﹣ $\frac{1}{2}$ ．
（1）若0＜α＜ $\frac{π}{2}$ ，且sinα= $\frac{\sqrt{2}}{2}$ ，求f（α）的值；
（2）求函数f（x）的最小正周期及单调递增区间．

查看试题解析
17.
在平面四边形ABCD中，AB=BD=CD=1，AB⊥BD，CD⊥BD，将△ABD沿BD折起，使得平面ABD⊥平面BCD，如图．
（1）求证：AB⊥CD；
（2）若M为AD中点，求直线AD与平面MBC所成角的正弦值．

查看试题解析
18. 为回馈顾客，某商场拟通过摸球兑奖的方式对1000位顾客进行奖励，规定：每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球，球上所标的面值之和为该顾客所获的奖励额．
（1）若袋中所装的4个球中有1个所标的面值为50元，其余3个均为10元，求：
①顾客所获的奖励额为60元的概率；
②顾客所获的奖励额的分布列及数学期望；
（2）商场对奖励总额的预算是60000元，并规定袋中的4个球只能由标有面值10元和50元的两种球组成，或标有面值20元和40元的两种球组成．为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡，请对袋中的4个球的面值给出一个合适的设计，并说明理由．

查看试题解析
19.
已知双曲线E： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的两条渐近线分别为l₁：y=2x，l₂：y=﹣2x．
（1）求双曲线E的离心率；
（2）如图，O为坐标原点，动直线l分别交直线l₁ ， l₂于A，B两点（A，B分别在第一、第四象限），且△OAB的面积恒为8，试探究：是否存在总与直线l有且只有一个公共点的双曲线E？若存在，求出双曲线E的方程，若不存在，说明理由．

查看试题解析
20. 已知函数f（x）=e^x﹣ax（a为常数）的图象与y轴交于点A，曲线y=f（x）在点A处的切线斜率为﹣1．
（Ⅰ）求a的值及函数f（x）的极值
（Ⅱ）证明：当x＞0时，x²＜e^x ．
（Ⅲ）证明：对任意给定的正数c，总存在x₀ ，使得当x∈（x₀ ， +∞），恒有x²＜ce^x ．

查看试题解析
21. 已知矩阵A的逆矩阵A^﹣1= $(\begin{matrix} 2 & 1 \\ 1 & 2 \end{matrix})$ ．
（1）求矩阵A；
（2）求矩阵A^﹣1的特征值以及属于每个特征值的一个特征向量．

查看试题解析
22. 已知直线l的参数方程为 $\{\begin{matrix} x = a - 2 t \\ y = - 4 t \end{matrix}$ （t为参数），圆C的参数方程为 $\{\begin{matrix} x = 4 \cos θ \\ y = 4 \sin θ \end{matrix}$ （θ为常数）．
（1）求直线l和圆C的普通方程；
（2）若直线l与圆C有公共点，求实数a的取值范围．

查看试题解析
23. 已知定义域在R上的函数f（x）=|x+1|+|x﹣2|的最小值为a．
（1）求a的值；
（2）若p，q，r为正实数，且p+q+r=a，求证：p²+q²+r²≥3．

查看试题解析