高中数学人教A版(2019)必修二 第六章 平面向量的概念与运算(二)
试卷更新日期:2021-03-24 类型:同步测试
一、单选题
-
1. 已知向量a,b满足 , , ,则 ( )A、 B、 C、 D、2. 如图,在底面为正方形的平行六面体 的棱中,与向量 模相等的向量有( ).
 A、0个 B、3个 C、7个 D、9个3. 下列关于空间向量的命题中,正确命题的个数是( )
A、0个 B、3个 C、7个 D、9个3. 下列关于空间向量的命题中,正确命题的个数是( )
(1)长度相等、方向相同的两个向量是相等向量;(2)平行且模相等的两个向量是相等向量;(3)若 ,则 ;(4)两个向量相等,则它们的起点与终点相同.A、0 B、1 C、2 D、34. 若平面向量 , 满足 ,则对于任意实数 , 的最小值是( )A、 B、 C、2 D、15. 已知向量 , 是两个不共线的向量,且向量m 3 与 (2﹣m) 共线,则实数m的值为( )A、﹣1或3 B、 C、﹣1或4 D、3或46. 如图, , 与 的夹角为 , 与 的夹角为 ,若 ,则 等于( ). A、 B、 C、 D、2
A、 B、 C、 D、2二、多选题
-
7. 在△ABC中,下列结论正确的是( )A、 ; B、 ; C、若 ,则△ABC是锐角三角形 D、若 ,则△ABC是等腰三角形;8. 是边长为2的等边三角形,已知向量 、 满足 、 ,则下列结论正确的是( )A、 B、 C、 D、9. 设 、 是两个非零向量,则下列描述正确的有( )A、若 ,则存在实数 使得 B、若 ,则 C、若 ,则 在 方向上的投影向量为 D、若存在实数 使得 ,则10. 在给出的下列命题中,正确的是( )A、设 是同一平面上的四个点,若 ,则点 必共线 B、若向量 是平面 上的两个向量,则平面 上的任一向量 都可以表示为 ,且表示方法是唯一的 C、已知平面向量 满足 则 为等腰三角形 D、已知平面向量 满足 ,且 ,则 是等边三角形
三、填空题
-
11. 已知平面向量 与 的夹角为 , 在 上的投影是 ,且满足 ,则 .12. 在△ABC中,∠A=60°,AB=3,AC=2.若 =2 , =λ ﹣ (λ∈R),且 =﹣4,则λ的值为 .13. 已知向量 、 满足| |=1,| |=2,则| + |+| ﹣ |的最小值是 , 最大值是 .14. 如图,在边长1为正方形 中, , 分别是 , 的中点,则 , 若 ,则 .
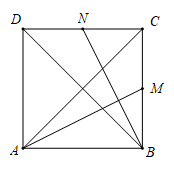 15. 计算: .16. 已知向量 、 ,且 , , ,则A、B、 C 、 D 四点中一定共线的三点是.
15. 计算: .16. 已知向量 、 ,且 , , ,则A、B、 C 、 D 四点中一定共线的三点是.四、解答题
-
17. 如图所示,已知 , , , , , ,试用 、 、 、 、 、 表示下列各式:
 (1)、 ;(2)、 ;(3)、 .18. 已知 是两个单位向量.(1)、若 ,试求 的值;(2)、若 的夹角为 ,求向量 在 上的投影.
(1)、 ;(2)、 ;(3)、 .18. 已知 是两个单位向量.(1)、若 ,试求 的值;(2)、若 的夹角为 ,求向量 在 上的投影.