重庆市云阳县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. 若分式 有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 已知长度分别为 , , 的三根小棒可以摆成一个三角形,则 的值不可能是( )A、2.4 B、3 C、5 D、8.55. 下列说法正确的是( )A、任意的三角形都是轴对称图形 B、轴对称图形只有一条对称轴 C、若两个三角形全等,则它们的周长也相等 D、有一边对应相等的两个等腰三角形是全等三角形6. 按如图所示的运算程序,当输入 , 时,输出的结果为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 已知长度分别为 , , 的三根小棒可以摆成一个三角形,则 的值不可能是( )A、2.4 B、3 C、5 D、8.55. 下列说法正确的是( )A、任意的三角形都是轴对称图形 B、轴对称图形只有一条对称轴 C、若两个三角形全等,则它们的周长也相等 D、有一边对应相等的两个等腰三角形是全等三角形6. 按如图所示的运算程序,当输入 , 时,输出的结果为( ) A、1 B、2 C、3 D、97. 如图, 、 分别为 、 边上的点, , .若 , ,则 的长度为( )
A、1 B、2 C、3 D、97. 如图, 、 分别为 、 边上的点, , .若 , ,则 的长度为( ) A、2 B、3 C、4 D、58. 下列等式中,从左到右的变形是分解因式的是( )A、 B、 C、 D、9. 如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )
A、2 B、3 C、4 D、58. 下列等式中,从左到右的变形是分解因式的是( )A、 B、 C、 D、9. 如图,在 中, , 是 的角平分线,若 ,则点 到 边的距离为( )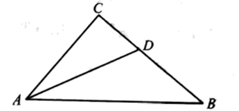 A、1 B、 C、2 D、310. 若计算 所得的结果中不含 的一次项,则常数 的值为( )A、-2 B、-1 C、0 D、211. 如图,在 中, , , 交 于点 ,若 ,则 的长度为( )
A、1 B、 C、2 D、310. 若计算 所得的结果中不含 的一次项,则常数 的值为( )A、-2 B、-1 C、0 D、211. 如图,在 中, , , 交 于点 ,若 ,则 的长度为( ) A、3.6 B、3.2 C、3 D、2.812. 若关于 的不等式组 有解,关于 的分式方程 有整数解,则符合条件的所有整数 的和为( )A、0 B、1 C、2 D、5
A、3.6 B、3.2 C、3 D、2.812. 若关于 的不等式组 有解,关于 的分式方程 有整数解,则符合条件的所有整数 的和为( )A、0 B、1 C、2 D、5二、填空题
-
13. 2020年12月17日,探月工程嫦娥五号返回器在内蒙古四子王旗预定区域成功着陆,标志着我国首次地外天体采样返回任务圆满完成.月球与地球近地点的距离约是363000000米,数据363000000用科学记数法表示为.14. 分解因式: .15. 当 时,分式 的值为0.16. 已知 ,则 .17. 如图,平面直角坐标系中,已知点 ,点 、 分别在 轴、 轴上, 且 ,若 点坐标为 ,则 (用含 的代数式表示).
 18. 如图,在 中, , 为 边中点, 为 边上一点,将 沿着 翻折,得到 ,连接 .当 时, 的度数为.
18. 如图,在 中, , 为 边中点, 为 边上一点,将 沿着 翻折,得到 ,连接 .当 时, 的度数为.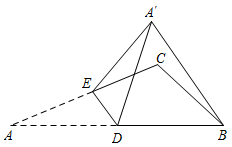
三、解答题
-
19.(1)、分解因式:(2)、计算:20.(1)、计算:(2)、解方程:21. 已知 三个顶点的坐标分别为 、 、 , 与 关于 轴对称,点 、 、 分别是点 、 、 的对应点.
 (1)、请在图中画出 ,并直接写出点 的坐标;(2)、连接 、 ,求 的面积.22. 先化简,再求值: ,其中 .23. 我国古代民间把正月正、二月二、三月三、五月五、六月六、七月七、九月九这“七重”列为吉庆日;“七”在生活中表现为时间的阶段性,比如一周有“七天”……在数的学习过程中,有一类自然数具有的特性也和“七”有关.
(1)、请在图中画出 ,并直接写出点 的坐标;(2)、连接 、 ,求 的面积.22. 先化简,再求值: ,其中 .23. 我国古代民间把正月正、二月二、三月三、五月五、六月六、七月七、九月九这“七重”列为吉庆日;“七”在生活中表现为时间的阶段性,比如一周有“七天”……在数的学习过程中,有一类自然数具有的特性也和“七”有关.定义:对于四位自然数 ,若其千位数字与个位数字之和等于7,百位数字与十位数字之和也等于7,则称这个四位自然数 为“七巧数”.
例如:3254是“七巧数”,因为 , ,所以3254是“七巧数”; 1456不是“七巧数”,因为 ,但 ,所以1456不是“七巧数”.
(1)、若一个“七巧数”的千位数字为 ,则其个位数字可表示为(用含 的代数式表示);(2)、最大的“七巧数”是 , 最小的“七巧数”是;(3)、若 是一个“七巧数”,且 的千位数字加上十位数字的和,是百位数字减去个位数字的差的3倍,请求出满足条件的所有“七巧数” .24. 如图, 和 均为等边三角形,连接 并延长,交 于点 ,连接 并延长,交 于点 ,连接 . (1)、求证: ;(2)、若 ,求证: .25. 为做好新冠肺炎疫情防控,某学校购入了一批洗手液与消毒液.购买洗手液花费3200元,购买消毒液花费3000元,购买的洗手液瓶数是消毒液瓶数的2倍,每瓶消毒液的价格比每瓶洗手液的价格高7元.(1)、求一瓶洗手液的价格与一瓶消毒液的价格分别是多少元?(2)、入冬以后,常见呼吸道传染病进入高发期,加剧了疫情防控的复杂性,学校决定第二次购入一批洗手液与消毒液,洗手液和消毒液的瓶数分别都比第一次的购入量多100瓶.适逢经销商进行价格调整,每瓶洗手液的价格比第一次的价格降低 ,每瓶消毒液的价格比第一次的价格降低 ,最终第二次购买洗手液与消毒液的总费用只比第一次购买洗手液 与消毒液的总费用多400元,求 的值.26. 如图,在 中, , ,垂足为 , 是 边上一点,过点 作 ,垂足为 ,连接 , 为 的中点.
(1)、求证: ;(2)、若 ,求证: .25. 为做好新冠肺炎疫情防控,某学校购入了一批洗手液与消毒液.购买洗手液花费3200元,购买消毒液花费3000元,购买的洗手液瓶数是消毒液瓶数的2倍,每瓶消毒液的价格比每瓶洗手液的价格高7元.(1)、求一瓶洗手液的价格与一瓶消毒液的价格分别是多少元?(2)、入冬以后,常见呼吸道传染病进入高发期,加剧了疫情防控的复杂性,学校决定第二次购入一批洗手液与消毒液,洗手液和消毒液的瓶数分别都比第一次的购入量多100瓶.适逢经销商进行价格调整,每瓶洗手液的价格比第一次的价格降低 ,每瓶消毒液的价格比第一次的价格降低 ,最终第二次购买洗手液与消毒液的总费用只比第一次购买洗手液 与消毒液的总费用多400元,求 的值.26. 如图,在 中, , ,垂足为 , 是 边上一点,过点 作 ,垂足为 ,连接 , 为 的中点. (1)、如图,过点 作 交 于点 ,若 , ,求 的度数;(2)、如图,若 ,过点 作 ,垂足为 .求证: .
(1)、如图,过点 作 交 于点 ,若 , ,求 的度数;(2)、如图,若 ,过点 作 ,垂足为 .求证: .