重庆市綦江区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. 下列四个标志是关于安全警示的标志,在这些标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 已知点B、C、F、E共线, , ,要使 ,还需补充一个条件,下列选项中不能满足要求的是( )
2. 若分式 有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 已知点B、C、F、E共线, , ,要使 ,还需补充一个条件,下列选项中不能满足要求的是( ) A、 B、 C、 D、5. 已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A、 B、 C、 D、5. 已知等腰三角形的两边长分别为3和6,则它的周长等于( )
A、12 B、12或15 C、15 D、15或186. 如图,△ABC中,AB=AC=10,DE是AB的中垂线,△BDC的周长为16,则BC长为( )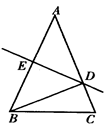 A、5 B、6 C、8 D、107. 已知 , , ( )A、12 B、108 C、18 D、368. 下列各选项中,因式分解正确的是( )A、 B、 C、 D、9. 方程 的增根为( )A、1 B、1和-1 C、-1 D、010. 下列图形都是由同样大小的矩形按一定的规律组成,其中,第1个图形中一共有6个矩形,第2个图形中一共有11个矩形,第3个图形中一共有16个矩形,…,按此规律,第7个图形中矩形的个数为( )
A、5 B、6 C、8 D、107. 已知 , , ( )A、12 B、108 C、18 D、368. 下列各选项中,因式分解正确的是( )A、 B、 C、 D、9. 方程 的增根为( )A、1 B、1和-1 C、-1 D、010. 下列图形都是由同样大小的矩形按一定的规律组成,其中,第1个图形中一共有6个矩形,第2个图形中一共有11个矩形,第3个图形中一共有16个矩形,…,按此规律,第7个图形中矩形的个数为( ) A、30 B、36 C、41 D、4511. 若数a关于x的不等式组 恰有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、2 B、3 C、4 D、512. 如图,在 中, 的面积为10, ,BD平分 ,E、F分别为BC、BD上的动点,则 的最小值是( )
A、30 B、36 C、41 D、4511. 若数a关于x的不等式组 恰有三个整数解,且使关于y的分式方程 的解为正数,则所有满足条件的整数a的值之和是( )A、2 B、3 C、4 D、512. 如图,在 中, 的面积为10, ,BD平分 ,E、F分别为BC、BD上的动点,则 的最小值是( )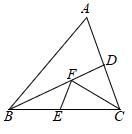 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 冬季流感病毒爆发的高峰期,流行性感冒病简称流感病毒,流感病毒可引起人、禽、猪、马、蝙蝠等多种动物感染和发病,是人流感、禽流感、猪流感、马流感等人与动物疫病的病原,“綦江少年,健康少年”,请綦江少年们注意保暖,多喝热水,开窗通风,防范流感病,以免生病,已知流感病毒的直径为0.00000009米,请将0.00000009米用科学记数法表示为米.14. 因式分解: ; .15. 若 是一个完全平方式,则k等于.16. A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程.17. 如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,……照这样走下去,他第一次回到出发地A点时,一共走了米。
 18. 金秋十月,丹桂飘香,重庆市綦江区某中学举行了创新科技大赛,该校初二年级某班共有18人报名参加航海组、航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于5人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6939元,则其中购买无人机模型的费用是.
18. 金秋十月,丹桂飘香,重庆市綦江区某中学举行了创新科技大赛,该校初二年级某班共有18人报名参加航海组、航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于5人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6939元,则其中购买无人机模型的费用是.三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 计算:(1)、 ;(2)、 .21. 如图, 在平面直角坐标系中,点 的坐标为(-3,1).
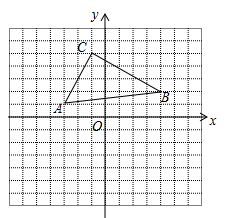 (1)、请在图中作出与 关于 轴对称的 ;(2)、写出点 , , 的坐标;(3)、求出 的面积.22. 如图, , , ,垂足为E, ,垂足为F.
(1)、请在图中作出与 关于 轴对称的 ;(2)、写出点 , , 的坐标;(3)、求出 的面积.22. 如图, , , ,垂足为E, ,垂足为F.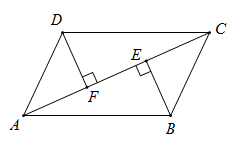
求证:
(1)、 ;(2)、 .23. 有一个三位数,其百位数字为a,十位数字为b,个位数字为c.若这个三位数百位数字的4倍加上十位数字的2倍,再加上个位数字的和能被8整除,则称这个三位数是“航天数”.如:232, ,故232是“航天数”.(1)、请你写出最小的三位“航天数”;并判断448是否是“航天数”;(2)、请证明任何一个三位“航天数”能被8整除,24. 如图,在 中, , 、 的平分线分别交AC、AB于点D、E,CE、BD相交于点F,连接DE. (1)、若 ,求DE的长;(2)、求证: .25. 轻轨3号线北延伸段渝北空港广场站的一项挖土工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲工程队工程款2.1万元,付乙工程队工程款1.5万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
(1)、若 ,求DE的长;(2)、求证: .25. 轻轨3号线北延伸段渝北空港广场站的一项挖土工程招标时,接到甲、乙两个工程队的投标书,每施工一天,需付甲工程队工程款2.1万元,付乙工程队工程款1.5万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:(方案一)甲队单独完成这项工程,刚好按规定工期完成;
(方案二)乙队单独完成这项工程要比规定工期多用5天;
(方案三)若由甲、乙两队合作做4天,剩下的工程由乙队单独做,也正好按规定工期完工.
(1)、请你求出完成这项工程的规定时间;(2)、如果你是工程领导小组的组长,为了节省工程款,同时又能如期完工,你将选择哪一种方案?说明理由.26. 请认真阅读下面的数学小探究系列,完成所提出的问题:
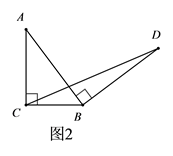
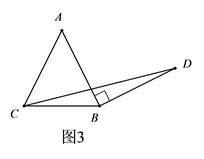 (1)、探究1,如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作BC边上的高DE,则DE与BC的数量关系是 , 的面积为;(2)、探究2,如图2,在一般的 中, , ( , ),将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含m,n的式子表示 的面积,并说明理由.(3)、探究3:如图3,在等腰三角形ABC中, , ( , , ),将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a,b,c的式子表示 的面积,要有探究过程.
(1)、探究1,如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作BC边上的高DE,则DE与BC的数量关系是 , 的面积为;(2)、探究2,如图2,在一般的 中, , ( , ),将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含m,n的式子表示 的面积,并说明理由.(3)、探究3:如图3,在等腰三角形ABC中, , ( , , ),将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a,b,c的式子表示 的面积,要有探究过程.