浙江省宁波市镇海区七校2020-2021学年八年级上学期数学期末联考试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. 下列四个图形中,是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的三边长分别为2、x、10,若x为正整数,则这样的三角形个数为( )A、1 B、2 C、3 D、43. 下列说法中正确的是( )A、使式子 有意义的是x>﹣3 B、使 是正整数的最小整数n是3 C、若正方形的边长为3 cm,则面积为30cm2 D、计算3÷ × 的结果是34. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,BE=CF,AB=DE,添加下列哪一个条件可以推证△ABC≌△DEF( )
2. 已知三角形的三边长分别为2、x、10,若x为正整数,则这样的三角形个数为( )A、1 B、2 C、3 D、43. 下列说法中正确的是( )A、使式子 有意义的是x>﹣3 B、使 是正整数的最小整数n是3 C、若正方形的边长为3 cm,则面积为30cm2 D、计算3÷ × 的结果是34. 若点P在一次函数 的图象上,则点P一定不在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,BE=CF,AB=DE,添加下列哪一个条件可以推证△ABC≌△DEF( ) A、BC=EF B、∠A=∠D C、AC//DF D、∠B=∠DEF6. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A、BC=EF B、∠A=∠D C、AC//DF D、∠B=∠DEF6. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( ) A、40° B、45° C、47.5° D、50°7. 关于 的不等式 只有2个正整数解,则 的取值范围为( )A、 B、 C、 D、8. 已知一次函数 和 ( 且 ),这两个函数的图象可能是( )A、
A、40° B、45° C、47.5° D、50°7. 关于 的不等式 只有2个正整数解,则 的取值范围为( )A、 B、 C、 D、8. 已知一次函数 和 ( 且 ),这两个函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,过点 作y轴的垂线交直线 于点 ,过点 作直线l的垂线,交y轴于点 ,过点 作y轴的垂线交直线l于点 ,…,这样依次下去,得到 , , ,…,其面积分别记为 , , ,…,则 ( )
9. 如图,过点 作y轴的垂线交直线 于点 ,过点 作直线l的垂线,交y轴于点 ,过点 作y轴的垂线交直线l于点 ,…,这样依次下去,得到 , , ,…,其面积分别记为 , , ,…,则 ( )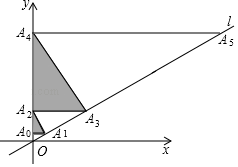 A、 B、 C、 D、10. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )
A、 B、 C、 D、10. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )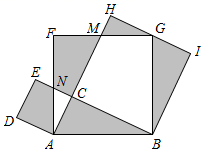 A、3 B、 C、2 D、
A、3 B、 C、2 D、二、填空题
-
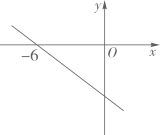
11. 命题“对顶角相等”的逆命题是12. 一次函数y=(2m-6)x+5中,y随x的增大而减小,则m的取值范围是 .13. 将点P(﹣2,﹣3)向左平移3个长度单位,再向上平移2个长度单位得到点Q,则点Q的坐标是.14. 已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为.
 15. 如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为.
15. 如图在△ABC中,∠ACB=90°,∠BAC=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°),得到△A′B′C,设A′C交AB边于D,连结AA′,若△AA′D是等腰三角形,则旋转角α的度数为. 16. 如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB交于点A′,连接AC′,若AD=AC′=4,BD=6,则点D到BC的距离为.
16. 如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB交于点A′,连接AC′,若AD=AC′=4,BD=6,则点D到BC的距离为.
三、解答题
-
17. 解下面一元一次不等式组,并写出它的所有非负整数解.
.
18. 计算:(1)、(2)、已知| ﹣a|+ =0,求a2﹣2 +2+b2的值.19. 如图,已知△ABC中,AB=AC,BD,CE是高,BD与CE相交于点O (1)、求证:OB=OC;(2)、若∠ABC=50°,求∠BOC的度数.20. 如图,在8×8网格纸中,每个小正方形的边长都为1.
(1)、求证:OB=OC;(2)、若∠ABC=50°,求∠BOC的度数.20. 如图,在8×8网格纸中,每个小正方形的边长都为1. (1)、请在网格纸中建立平面直角坐标系,使点A、C的坐标分别为(-4,4),(-1,3),并写出点B的坐标为;(2)、①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;
(1)、请在网格纸中建立平面直角坐标系,使点A、C的坐标分别为(-4,4),(-1,3),并写出点B的坐标为;(2)、①画出△ABC关于y轴的对称图形△A1B1C1 , 并写出B1点的坐标;②在y轴上求作一点P,使△PAB的周长最小,并直接写出点P的坐标
21. 某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题: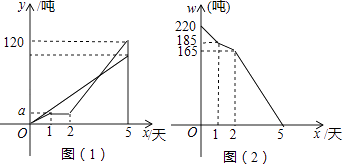 (1)、甲车间每天加工大米吨,a= .
(1)、甲车间每天加工大米吨,a= .
(2)、求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)、若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?22. 某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)、设装运甲种土特产的车辆数为 ,装运乙种土特产的车辆数为 ,求 与 之间的函数关系式.(2)、如果装运每辆土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)、若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.23. 我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.(1)、●特例感知
①等腰直角三角形 △ 勾股高三角形(请填写“是”或者“不是”);②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若 ,试求线段CD的长度.
 (2)、●深入探究
(2)、●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明; (3)、●推广应用
(3)、●推广应用
如图3,等腰△ABC为勾股高三角形,其中 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若 ,试求线段DE的长度. 24. 如图(1),在平面直角坐标系中,直线 交坐标轴于A、B两点,过点C( ,0)作CD交AB于D,交 轴于点E.且△COE≌△BOA.
24. 如图(1),在平面直角坐标系中,直线 交坐标轴于A、B两点,过点C( ,0)作CD交AB于D,交 轴于点E.且△COE≌△BOA. (1)、求B点坐标为;线段OA的长为;(2)、确定直线CD解析式,求出点D坐标;(3)、如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
(1)、求B点坐标为;线段OA的长为;(2)、确定直线CD解析式,求出点D坐标;(3)、如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.