四川省眉山市东坡区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-24 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、 2 B、-2 C、±2 D、± $\sqrt{2}$

查看试题解析
2. 要反映杭州市3月份气温的变化情况宜采用（）

A、条形统计图 B、折线统计图 C、扇形统计图 D、频数直方图

查看试题解析
3. 下列运算正确的是（）

A、 $a \cdot a^{2} = a^{2}$ B、 ${(a b)}^{2} = a b^{2}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
4. 下列因式分解正确的是（　　）

A、x²﹣4=（x+4）（x﹣4） B、x²+2x+1=x（x+2）+1 C、3mx﹣6my=3m（x﹣6y） D、2x+4=2（x+2）

查看试题解析
5. 如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（）

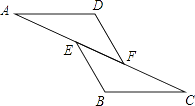A、∠A=∠C B、AD=CB C、BE=DF D、AD∥BC

查看试题解析
6. 已知 $3^{x} = 2, 3^{y} = 3$ ，则 $3^{x + y}$ 的值为（）

A、6 B、5 C、36 D、3

查看试题解析
7. 满足下列条件的△ABC不是直角三角形的是（）

A、AC＝1，BC＝ $\sqrt{3}$ ，AB＝2 B、AC：BC：AB＝3：4：5 C、∠A：∠B：∠C＝1：2：3 D、∠A：∠B：∠C＝3：4：5

查看试题解析
8. 给出下列命题：（1）有两条边对应相等的两个直角三角形一定全等；（2） $\sqrt{11}$ 的整数部分是3，小数部分是 $\sqrt{11} - 3$ ；（3）平方根等于本身的数是0、1；（4）等腰三角形两条边的长度分别为1和3，则它的周长为5或7.其中真命题的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 若m为常数，要使 $9 x^{2} + m x + 1$ 成为完全平方式，那么m的值是（）

A、-6 B、±6 C、6 D、±3

查看试题解析
10. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \cdot \cdot \cdot (2^{1010} + 1)$ 化简的结果为（）

A、 $2^{1010} - 1$ B、 $2^{1010} + 1$ C、 $2^{2020} - 1$ D、 $2^{2020} + 1$

查看试题解析
11. 如图，在Rt△ABC中，∠C=90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”.当AC=4，BC=3时，则阴影部分的面积为（）

A、6 B、 $6 π$ C、 $\frac{5}{2} π$ D、12

查看试题解析
12. 如图，在△ABC中，AB=AC，∠BAC=64°，∠BAC的平分线与AB的垂直平分线交于点O，点E、F分别在BC、AC上，点C沿EF折叠后与点O重合，则∠BEO的度数是（）

A、26° B、32° C、52° D、58°

查看试题解析

二、填空题

13. 已知数据： $\frac{1}{2}$ ， $\sqrt{5}$ ，π， $\sqrt{4}$ ，0，其中无理数出现的频率为.

查看试题解析
14. 因式分解： $x^{2} - x - 12 =$ ．

查看试题解析
15. 如果 $(x - 1) (x^{2} - 2 m x + m)$ 的乘积中不含 $x^{2}$ 项，则m的值为.

查看试题解析
16. 如图，在△ABC中，AB=AC ， AB的垂直平分线DE交AB于点D ，交AC于点E ，若△ABC与△EBC的周长分别是22、14，则AC的长是．

查看试题解析
17. 在 $Δ$ ABC中，AB=3，AC=4，则BC边上的中线AD的取值范围是

查看试题解析
18. 如图，在Rt△ABC中，∠ACB=90°，BC=4cm，AC=3cm，动点P从点B出发沿射线BA以2cm/s的速度运动.设运动时间为t，则当t=秒时，△BPC为直角三角形.

查看试题解析

三、解答题

19. 计算： $| - \frac{1}{2} | - \sqrt[3]{- 27} + {(- 1)}^{2020} - \sqrt{16}$ .

查看试题解析
20. 先化简，再求值： $[(- x + 2 y) (- x - 2 y) + {(- 3 x + 2 y)}^{2}] \div (- \frac{1}{2} x)$ ，其中 $x = 1$ ， $y = \frac{1}{2}$ .

查看试题解析
21. 如图，已知AB $//$ CF，D是AB上一点，DF交AC于点E，DE＝EF.求证：AB＝BD+CF.

查看试题解析
22. 小东和小明要测量校园里的一块四边形场地 $A B C D$ (如图所示)的周长，其中边 $C D$ 上有水池及建筑遮挡，没有办法直接测量其长度.小东经测量得知 $A B = A D = 15$ 米， $∠ A = 60 ° ， B C = 20$ 米， $∠ A B C = 150 °$ .小明说根据小东所得的数据可以求出 $C D$ 的长度.你同意小明的说法吗？若同意，请求出 $C D$ 的长度；若不同意，请说明理由.

查看试题解析
23. “天府通办”APP是一款服务于四川人民群众的手机应用平台，某社区从2020年11月开始试运行该APP.某数学活动小组就此APP在该社区居民中的用户满意度进行了问卷调查，问卷调查的结果分为 “非常好”、“较好”、“一般”、“较差”四个等级，分别记作A、B、C、D.根据调查结果绘制出如图所示的扇形统计图和条形统计图.
请结合图中所给信息解答下列问题：

(1)、本次被调查的对象共有人，结果“一般”出现的频数是，频率是；

(2)、写出扇形统计图中，表示“较好”扇形的圆心角的度数，并将条形统计图补充完整；

(3)、若该社区共有群众80000人，请估计该社区群众对此APP满意度为“非常好”的人数.

查看试题解析
24. 观察下列分解因式的过程： $a^{2} + 2 a b - 3 b^{2}$ .
解：原式= $a^{2} + 2 a b + b^{2} - b^{2} - 3 b^{2}$

$= (a^{2} + 2 a b + b^{2}) - 4 b^{2}$

$= {(a + b)}^{2} - {(2 b)}^{2}$

$= (a + b + 2 b) (a + b - 2 b)$

$= (a + 3 b) (a - b)$

像这种通过增减项把多项式转化成完全平方形式的方法称为配方法.

(1)、请你运用上述配方法分解因式： $a^{2} + 4 a b - 5 b^{2}$ ；

(2)、代数式 $a^{2} + 2 a + b^{2} - 6 b + 12$ 是否存在最小值？如果存在，请求出当a、b分别是多少时，此代数式存在最小值，最小值是多少？如果不存在，请说明理由.

查看试题解析
25. 如图，在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 4$ ， $A C = 3$ ， $D E$ 垂直平分 $A B$ ，分别交 $A B$ ， $B C$ 于点 $D$ ， $E$ ， $A P$ 平分 $∠ B A C$ ，与 $D E$ 的延长线交于点 $P$ .

(1)、求 $P D$ 的长度；

(2)、连接 $P C$ ，求 $P C$ 的长度.

查看试题解析
26. 在△ABC中，AB=AC，∠BAC=90，BD平分∠ABC交AC于点D.

(1)、如图1，点F为BC上一点，连接AF交BD于点E.若AB=BF，求证：BD垂直平分AF.

(2)、如图2，CE⊥BD，垂足E在BD的延长线上.试判断线段CE和BD的数量关系，并说明理由.

(3)、如图3，点F为BC上一点，∠EFC= $\frac{1}{2}$ ∠ABC，CE⊥EF，垂足为E，EF与AC交于点M.直接写出线段CE与线段FM的数量关系.

查看试题解析