四川省成都市武侯区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. 三个正方形的面积如图所示,则S的值为( )
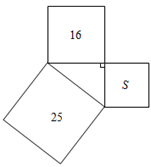 A、3 B、4 C、9 D、122. 下列图象中,表示y是x的函数的是( )A、
A、3 B、4 C、9 D、122. 下列图象中,表示y是x的函数的是( )A、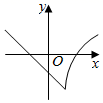 B、
B、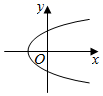 C、
C、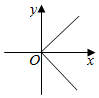 D、
D、 3. 在平面直角坐标系中.点 关于x轴对称的点的坐标是( )A、 B、 C、 D、4. 如图,数轴上有M,N,P,Q四点,则这四点中所表示的数最接近﹣ 的是( )
3. 在平面直角坐标系中.点 关于x轴对称的点的坐标是( )A、 B、 C、 D、4. 如图,数轴上有M,N,P,Q四点,则这四点中所表示的数最接近﹣ 的是( ) A、点M B、点N C、点P D、点Q5. 下列计算正确的是( )A、 =2 B、 =3 C、 • = D、2 =36. 如图,AB CD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( )
A、点M B、点N C、点P D、点Q5. 下列计算正确的是( )A、 =2 B、 =3 C、 • = D、2 =36. 如图,AB CD,BE交AD于点E,若∠B=18°,∠D=32°,则∠BED的度数为( ) A、18° B、32° C、50° D、60°7. 我们把形如a +b(a,b为有理数, 为最简二次根式)的数叫做 型无理数,如3 +1是 型无理数,则( )2是( )A、 型无理数 B、 型无理数 C、 型无理数 D、 型无理数8. 已知等腰三角形的两边长分别为a,b,且a,b满足 +|b﹣4|=0,则此等腰三角形的周长为( )A、7 B、10 C、11 D、10或119. 如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则关于x,y的方程组 的解为( )
A、18° B、32° C、50° D、60°7. 我们把形如a +b(a,b为有理数, 为最简二次根式)的数叫做 型无理数,如3 +1是 型无理数,则( )2是( )A、 型无理数 B、 型无理数 C、 型无理数 D、 型无理数8. 已知等腰三角形的两边长分别为a,b,且a,b满足 +|b﹣4|=0,则此等腰三角形的周长为( )A、7 B、10 C、11 D、10或119. 如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则关于x,y的方程组 的解为( ) A、 B、 C、 D、10. 《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 .类似地,图2所示的算筹图我们可以表述为( )
A、 B、 C、 D、10. 《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1表示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 .类似地,图2所示的算筹图我们可以表述为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如果方程组 的解为 ,那么“*”表示的数是.12. 如图,在平面直角坐标系xOy中,以点A(﹣5,0)为圆心,13为半径作弧,交y轴的正半轴于点B,则点B的坐标为.
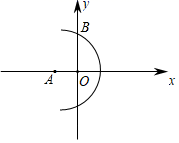 13. 武侯区某中学选拔一名学生参加区运动会的跳高项目,在10次测试中,甲、乙、丙、丁四名学生的跳高成绩的平均数均为1.6m,方差分别为: =0.48, =0.56, =0.52, =0.58,则这四名学生中成绩最稳定的是.14. 已知x= +2,y= ﹣2,则x2+y2+2xy=.15. 已知直线y=kx﹣3与y=(3k﹣1)x+2互相平行,则直线y=kx﹣3不经过第象限.16. 现将一支长20cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8cm,6cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为cm.17. 如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为.
13. 武侯区某中学选拔一名学生参加区运动会的跳高项目,在10次测试中,甲、乙、丙、丁四名学生的跳高成绩的平均数均为1.6m,方差分别为: =0.48, =0.56, =0.52, =0.58,则这四名学生中成绩最稳定的是.14. 已知x= +2,y= ﹣2,则x2+y2+2xy=.15. 已知直线y=kx﹣3与y=(3k﹣1)x+2互相平行,则直线y=kx﹣3不经过第象限.16. 现将一支长20cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8cm,6cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为cm.17. 如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为. 18. 在Rt△ACB中,∠ACB=90°,点D在边AB上,连接CD,将△ADC沿直线CD翻折,点A恰好落在BC边上的点E处,若AC=3,BE=1,则DE的长是.
18. 在Rt△ACB中,∠ACB=90°,点D在边AB上,连接CD,将△ADC沿直线CD翻折,点A恰好落在BC边上的点E处,若AC=3,BE=1,则DE的长是.
三、解答题
-
19. 计算:(1)、(π﹣2020)0﹣2 +|1﹣ |.(2)、 ﹣ .20. 解方程组: .21. 在平面直角坐标系xOy中,一次函数y=﹣x+6的图象分别交y轴和x轴于点A,B,交一次函数y=2x的图象于点C.
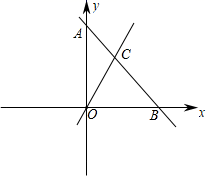 (1)、求点C的坐标;(2)、求△OBC的面积.22. 如图,在平面直角坐标系xOy中,已知点A(﹣1,5),B(1,0),C(3,1),连接BC.
(1)、求点C的坐标;(2)、求△OBC的面积.22. 如图,在平面直角坐标系xOy中,已知点A(﹣1,5),B(1,0),C(3,1),连接BC. (1)、在图中画出点A关于y轴的对称点 ,连接 ,并直接写出点 的坐标;(2)、在(1)的基础上,试判断△ 的形状,并说明理由.23. 第31届世界大学生夏季运动会计划于2021年8月在成都举行,武侯区某学校开展“爱成都,迎大运”活动的小主持人选拔赛,对A,B,C,D四名候选人进行了笔试和面试(各项成绩满分均为100分),他们的各项成绩如表所示:
(1)、在图中画出点A关于y轴的对称点 ,连接 ,并直接写出点 的坐标;(2)、在(1)的基础上,试判断△ 的形状,并说明理由.23. 第31届世界大学生夏季运动会计划于2021年8月在成都举行,武侯区某学校开展“爱成都,迎大运”活动的小主持人选拔赛,对A,B,C,D四名候选人进行了笔试和面试(各项成绩满分均为100分),他们的各项成绩如表所示:学生
笔试成绩/分
面试成绩/分
A
90
86
B
84
90
C
x
88
D
86
84
(1)、填空:这四名候选人的面试成绩的中位数是分;(2)、学校按笔试成绩占60%、面试成绩占40%的方式确定候选人的综合成绩(满分为100分),若候选人C的综合成绩为86.2分,求表中x的值;(3)、在(2)的条件下,分别求其余三名候选人的综合成绩,如果学校将根据综合成绩遴选两名小主持人,试问哪两名候选人将被录取?24. [阅读理解]如图,在△ABC中,AB=4,AC=6,BC=7,过点A作直线BC的垂线,垂足为D,求线段AD的长.

解:设BD=x,则CD=7﹣x.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,AD2=AB2﹣BD2 ,
在Rt△ACD中,AD2=AC2﹣CD2 ,
∴AB2﹣BD2=AC2﹣CD2.
又∵AB=4,AC=6,
∴42﹣x2=62﹣(7﹣x)2.
解得x= ,
∴BD= .
∴AD= = .
[知识迁移]
(1)、在△ABC中,AB=13,AC=15,过点A作直线BC的垂线,垂足为D.i)如图1,若BC=14,求线段AD的长;
ii)若AD=12,求线段BC的长.
(2)、如图2,在△ABC中,AB= ,AC= ,过点A作直线BC的垂线,交线段BC于点D,将△ABD沿直线AB翻折后得到对应的△ ,连接CD′,若AD= ,求线段 的长.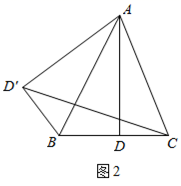 25. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:
25. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:种类
生产成本(元/件)
销售单价(元/件)
酒精消毒液
56
62
额温枪
84
100
(1)、若该公司2020年12月生产两种物资共100万件,生产总成本为7280万元,请用列二元一次方程组的方法,求该月酒精消毒液和额温枪两种物资各生产了多少万件?(2)、该公司2021年1月生产两种物资共150万件,根据市场需求,该月将举办迎新年促销活动,其中酒精消毒液的销售单价降低2元,额温枪打9折销售.若设该月生产酒精消毒液x万件,该月销售完这两种物资的总利润为y万元,求y与x之间的函数关系式.26. 在等腰直角三角形ABC中,∠ACB=90°,CD⊥AB于点D,点E是平面内任意一点,连接DE. (1)、如图1,当点E在边BC上时,过点D作DF⊥DE交AC于点F.
(1)、如图1,当点E在边BC上时,过点D作DF⊥DE交AC于点F.i)求证:CE=AF;
ii)试探究线段AF,DE,BE之间满足的数量关系.
(2)、如图2,当点E在△BDC内部时,连接AE,CE,若DB=5,DE=3 ,∠AED=45°,求线段CE的长.27. 在平面直角坐标系xOy中,已知点M(﹣2,﹣2),过点M作直线AB,交x轴负半轴于点A,交y轴负半轴于点B(0,m).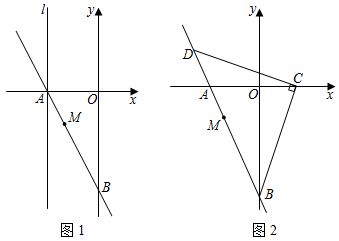 (1)、如图1,当m=﹣6时.
(1)、如图1,当m=﹣6时.i)求直线AB的函数表达式;
ii)过点A作y轴的平行线l,点N是l上一动点,连接BN,MN,若S△MBN= S△ABO , 求满足条件的点N的坐标.
(2)、如图2,将直线AB绕点B顺时针旋转45°后,交x轴正半轴于点C,过点C作CD⊥BC,交直线AB于点D.试问:随着m值的改变,点D的横坐标是否发生变化?若不变,求出点D的横坐标;若变化,请说明理由.