四川省成都市天府新区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-24 类型：期末考试

进入出卷网下载

一、单选题

1. 和数轴上的点一一对应的是（）

A、整数 B、有理数 C、无理数 D、实数

查看试题解析
2. 正比例函数y＝2x的图象必经过点（　　）

A、（﹣1，﹣2） B、（﹣1，2） C、（1，﹣2） D、（2，1）

查看试题解析
3. 下列各组数分别为一个三角形三边的长，其中不能构成直角三角形的一组是（）

A、8，10，12 B、3，4，5 C、5，12，13 D、7，24，25

查看试题解析
4. 已知关于x，y的二元一次方程组 ${\begin{matrix} 3 x + 2 y = k + 1 \\ x - 2 y = 9 \end{matrix}$ 的解为 ${\begin{matrix} x = 3 \\ y = - 3 \end{matrix}$ ，则k的值是（）

A、3 B、2 C、1 D、0

查看试题解析

5. 八年级（1）班甲、乙、丙、丁四名同学几次数学测试成绩的平均数（分）及方差如表，老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛，那么应选（）

	甲	乙	丙	丁
平均数（分）	95	97	95	97
方差	0.5	0.5	0.2	0.2

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 如图，在下列条件中，能判断AB∥CD的是（）

A、∠1＝∠2 B、∠BAD＝∠BCD C、∠BAD＋∠ADC＝180° D、∠3＝∠4

查看试题解析
7. 下列各数中，介于6和7之间的数是（）

A、 $\sqrt{7} + 2$ B、 $\sqrt{45}$ C、 $\sqrt{47} - 2$ D、 $\sqrt{35}$

查看试题解析
8. 为说明命题“若m＞n，则m²＞n²”是假命题，所列举反例正确的是（）

A、m＝6，n＝3 B、m＝0.2，n＝0.01 C、m＝1，n＝﹣6 D、m＝0.5，n＝0.3

查看试题解析
9. 若一次函数 $y = (k - 2) x + 1$ 的函数值 $y$ 随 $x$ 的增大而增大，则（）

A、 $k < 2$ B、 $k > 2$ C、 $k > 0$ D、 $k < 0$

查看试题解析
10. 如图，两直线 $y_{1} = k x + b$ 和 $y_{2} = b x + k$ 在同一坐标系内图象的位置可能是（）

A、 B、 C、 D、

查看试题解析

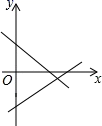
二、填空题

11. 若x³＝﹣ $\frac{8}{27}$ ，则x＝.

查看试题解析
12. 已知点A（2，m＋1）与B（﹣2，﹣3）关于y轴对称，则m＝.

查看试题解析
13. 已知 $\sqrt{a - 2} + {(b + 3)}^{2} = 0$ ，则（a﹣b）²＝．

查看试题解析
14. 《九章算术》是我国古代一部著名的算书，它的出现标志着中国古代数学形成了完整的体系其中卷八方程[七]中记载：“今有牛五、羊二，直金十两.牛二、羊五，直金八两.牛、羊各直金几何？”题目大意是：5头牛、2只羊共值金10两.2头牛、5只羊共值金8两.每头牛、每只羊各值金多少两？设1头牛值金 $x$ 两，1只羊值金 $y$ 两，则可列方程组为.

查看试题解析
15. 如图，AB=AC，则数轴上点C所表示的数为.

查看试题解析
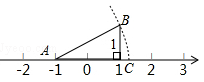16. 若点A（ $\frac{4}{3}$ ，m）和点B（n，﹣ $\frac{3}{2}$ ）在同一个正比例函数图象上，则﹣ $\frac{2}{m n}$ 的值是.

查看试题解析
17. 若x＝ $\sqrt{2}$ ﹣1，则x³＋x²﹣3x＋2035的值为.

查看试题解析
18. 当m，n是正实数，且满足m＋n＝mn时，就称点P（m， $\frac{m}{n}$ ）为“美好点”.已知点A（1，8）与点B的坐标满足y＝﹣x＋b，且点B是“美好点”，则△OAB的面积为.

查看试题解析
19. 如图，已知∠MON＝30°，B为OM上一点，BA⊥ON于A ，四边形ABCD为正方形，P为射线BM上一动点，连结CP ，将CP绕点C顺时针方向旋转90°得CE ，连结BE ，若AB＝ $\sqrt{3}$ ，则BE的最小值为．

查看试题解析

三、解答题

20.

(1)、计算： $\sqrt[3]{- 27}$ ＋（ $\frac{1}{2}$ ）^﹣²＋|2﹣ $\sqrt{3}$ |﹣ $\sqrt{9}$ ；

(2)、解方程组： ${\begin{matrix} 2 x - 3 y = 6 \\ x + 2 y = 10 \end{matrix}$ .

查看试题解析
21. 已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：AE∥PF.

查看试题解析
22. △ABC在平面直角坐标系中的位置如图所示，A，B，C三点在格点上.

（ 1）作出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁的坐标；

（ 2 ）在y轴上作点D，使得AD＋BD最小，并求出最小值.

查看试题解析
23. 天府新区某校在暑假期间开展了“趣自然阅当夏”活动，王华调查了本校50名学生本学期购买课外书的费用情况，数据如下表：

费用（元）

20

30

50

80

100

人数

6

10

14

12

8

(1)、这50名学生本学期购买课外书的费用的众数是，中位数是；

(2)、求这50名学生本学期购买课外书的平均费用；

(3)、若该校共有学生1000名，试估计该校本学期购买课外书费用在50元以上（含50元）的学生有多少名？

查看试题解析
24. 在疫情防控期间，某中学为保障广大师生生命健康安全，预从商场购进一批免洗手消毒液和84消毒液.如果购买40瓶免洗手消毒液和90瓶84消毒液，共需花费1320元，如果购买60瓶免洗手消毒液和120瓶84消毒液，共需花费1860元.

(1)、每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元？

(2)、若商场有两种促销方案：方案一，所有购买商品均打九折；方案二，购买5瓶免洗手消毒液送2瓶84消毒液，学校打算购进免洗手消毒液100瓶，84消毒液60瓶，请问学校选用哪种方案更节约钱？节约多少钱？

查看试题解析
25. 如图，平面直角坐标系中，A（0，a），B（b，0），OC＝OA，且a，b满足|a﹣8|＋ $\sqrt{b + 6}$ ＝0

(1)、求直线AB的表达式；

(2)、现有一动点P从点B出发，以1米/秒的速度沿x轴正方向运动到点C停止，设P的运动时间为t，连接AP，过点C作AP的垂线交射线AP于点M，交y轴于点N，请用含t的式子表示线段ON的长度；

(3)、在（2）的条件下，连接BM，当S_△ABM：S_△ACM＝3：7时，求此时P点的坐标.

查看试题解析
26. 甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示.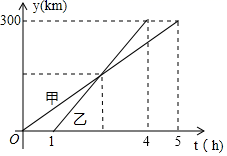

(1)、A，B两城相距千米，乙车比甲车早到小时；

(2)、甲车出发多长时间与乙车相遇？

(3)、若两车相距不超过30千米时可以通过无线电相互通话，则两车都在行驶过程中可以通过无线电通话的时间有多长？

查看试题解析
27. 如图，△ABC和△CEF中，∠BAC＝∠CEF＝90°，AB＝AC，EC＝EF，点E在AC边上.

(1)、如图1，连接BE，若AE＝3，BE＝ $\sqrt{58}$ ，求FC的长度；

(2)、如图2，将△CEF绕点C逆时针旋转，旋转角为α（0°＜α＜180°），旋转过程中，直线EF分别与直线AC，BC交于点M，N，当△CMN是等腰三角形时，求旋转角α的度数；

(3)、如图3，将△CEF绕点C顺时针旋转，使得点B，E，F在同一条直线上，点P为BF的中点，连接AE，猜想AE，CF和BP之间的数量关系并说明理由.

查看试题解析
28. 如图1，已知直线l₁：y＝kx＋b与直线l₂：y＝ $\frac{4}{3}$ x交于点M，直线l₁与坐标轴分别交于A，C两点，且点A坐标为（0，7），点C坐标为（7，0）.

(1)、求直线l₁的函数表达式；

(2)、在直线l₂上是否存在点D，使△ADM的面积等于△AOM面积的2倍，若存在，请求出点D的坐标，若不存在，请说明理由；

(3)、若点P是线段OM上的一动点（不与端点重合），过点P作PB∥x轴交CM于点B，设点P的纵坐标为m，以点P为直角顶点作等腰直角△PBF（点F在直线PB下方），设△PBF与△MOC重叠部分的面积为S，求S与m之间的函数关系式，并写出相应m的取值范围.

查看试题解析

费用（元）	20	30	50	80	100
人数	6	10	14	12	8