重庆市长寿区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. ﹣3的绝对值是( )A、﹣3 B、3 C、- D、2. 数轴上的点A到原点的距离是4,则点A表示的数为 ( )A、4 B、-4 C、4或-4 D、2或-23. 由四个大小相同的正方体组成的几何体如左图所示,从上往下看到的图形是( )
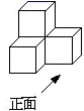 A、
A、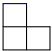 B、
B、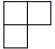 C、
C、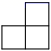 D、
D、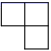 4. 的系数次数分别为( )A、 ,7 B、 ,6 C、 ,8 D、5π,65. 已知关于x的方程 的解是 ,则a的值为( )A、2 B、3 C、4 D、56. 下列计算正确的有( )
4. 的系数次数分别为( )A、 ,7 B、 ,6 C、 ,8 D、5π,65. 已知关于x的方程 的解是 ,则a的值为( )A、2 B、3 C、4 D、56. 下列计算正确的有( )① ; ② ;
③ ; ④ ;
⑤ .
A、1个 B、2个 C、3个 D、4个7. 如图,数轴上A、B两点分别对应数a、b,则下列各式正确的是( ) A、 B、 C、 D、8. 若 ,则代数式 的值是( )A、3 B、 C、 D、219. 某商店在出售某种商品时,以m元的价格出售,亏本50%,则在这次买卖中该商店的亏损情况是( )A、亏m元 B、亏50%m元 C、亏25%m元 D、亏50%元10. 某市为提倡节约用水,采取分段收费.若每户每月用水不超过 ,每立方米收费2元;若用水超过 ,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )A、 B、 C、 D、11. 已知关于x的方程x- -1的解是正整数,则符合条件的所有整数a的积是( )A、12 B、36 C、-4 D、-1212. 下列说法中,正确的个数有( )
A、 B、 C、 D、8. 若 ,则代数式 的值是( )A、3 B、 C、 D、219. 某商店在出售某种商品时,以m元的价格出售,亏本50%,则在这次买卖中该商店的亏损情况是( )A、亏m元 B、亏50%m元 C、亏25%m元 D、亏50%元10. 某市为提倡节约用水,采取分段收费.若每户每月用水不超过 ,每立方米收费2元;若用水超过 ,超过部分每立方米加收1元.小明家5月份交水费64元,则他家该月用水( )A、 B、 C、 D、11. 已知关于x的方程x- -1的解是正整数,则符合条件的所有整数a的积是( )A、12 B、36 C、-4 D、-1212. 下列说法中,正确的个数有( )①射线 和射线 是同一条射线;
②若 ,则点B为线段 的中点;
③同角的补角相等;
④点C在线段 上,M、N分别是线段 , 的中点.若 ,则线段 .
A、1个 B、2个 C、3个 D、4个二、填空题
-
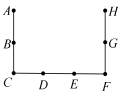
13. 北京奥运会国家体育场“鸟巢”的建筑面积为258000平方米,那么258000用科学记数法可表示为.14. 若 ,则 的余角的大小是.15. 若 与 是同类项,则 .16. 我们听过龟兔赛跑的故事,都知道乌龟最后战胜了小白兔.如果在第二次赛跑中,小白兔知耻而后勇,在落后乌龟600米时,以85米/分的速度奋起直追,而乌龟仍然以5米/分的速度爬行,那么小白兔需要分钟就能追上乌龟.17. 如图,已知点B、G分别是线段 、 的中点,点D、E是线段 的三等分点,如果 .那么图中所有线段的长的和为.
 18. 如图,圆上有五个点,这五个点将圆分成五等分(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从 为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从 为第2次“移位”.若小明从编号为4的点开始,第2024次“移位”后,他到达编号为的点.
18. 如图,圆上有五个点,这五个点将圆分成五等分(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5.若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,我们把这种走法称为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从 为第1次“移位”,这时他到达编号为1的点,那么他应走1段弧长,即从 为第2次“移位”.若小明从编号为4的点开始,第2024次“移位”后,他到达编号为的点.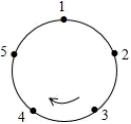
三、解答题
-
19. 计算: .20. 解方程: .21. 已知实数m使得多项式 化简后不含 项,求代数式 的值.22. 邮递员骑摩托车从邮局出发,先向南骑行 到达A村,继续向南骑行 到达B村,然后向北骑行 到达C村,最后回到邮局.(1)、以邮局为原点,以向北方向为正方向,用1个单位长度表示 ,画出数轴,并在数轴上表示出A、B、C三个村庄的位置.(2)、若摩托车每 耗油3升,汽油的单价是5.8元/升,求这趟路共耗油多少元?(精确到十分位).23. 某地出租车按实际租车里程收租车费,该地规定不足3公里统一收租车费10元,超过3公里(含3公里)后每超1公里加收租车费2.4元.(1)、若某人乘出租车x公里,租车费是多少元?(2)、若小明乘出租车的租车费为18.4元,他实际租车里程为多少公里?24. 如图,直线 、 相交于点O, 平分 , 平分 , .
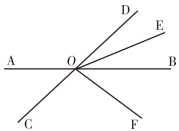 (1)、求 的度数;(2)、求 的度数.25. 一个n位数( ,n为正整数),我们把最高位上的数移到它的右侧,得到一个新数,再将新数的最高位上的数移到它的右侧,又得到一个新数,…,依次类推,我们把这样操作得到的新数都叫做原数的“谦虚数”.比如56有一个“谦虚数”是65;156有两个“谦虚数”分别是561、615;2834有三个“谦虚数”分别是8342、3428、4283.(1)、请写出四位数5832的三个“谦虚数”.(2)、一个两位数,个位上的数与十位上的数和为9,如果这个两位数比它的“谦虚数”少9,求这个两位数.(3)、一个三位数,百位上的数为a,十位上的数为1,个位上的数为b,如果这个三位数与它的两个“谦虚数”的和能被5整除,求 的值.26. 如图,已知数轴上点A表示的数为8,点B表示的数为 .动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为 秒.
(1)、求 的度数;(2)、求 的度数.25. 一个n位数( ,n为正整数),我们把最高位上的数移到它的右侧,得到一个新数,再将新数的最高位上的数移到它的右侧,又得到一个新数,…,依次类推,我们把这样操作得到的新数都叫做原数的“谦虚数”.比如56有一个“谦虚数”是65;156有两个“谦虚数”分别是561、615;2834有三个“谦虚数”分别是8342、3428、4283.(1)、请写出四位数5832的三个“谦虚数”.(2)、一个两位数,个位上的数与十位上的数和为9,如果这个两位数比它的“谦虚数”少9,求这个两位数.(3)、一个三位数,百位上的数为a,十位上的数为1,个位上的数为b,如果这个三位数与它的两个“谦虚数”的和能被5整除,求 的值.26. 如图,已知数轴上点A表示的数为8,点B表示的数为 .动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为 秒.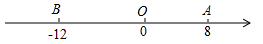 (1)、线段 的长为个单位长度,点P运动t秒后表示的数为(用含t的代数式表示);(2)、动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?(3)、若M为 的中点,N为 的中点.点P在运动的过程中,线段 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段 的长.
(1)、线段 的长为个单位长度,点P运动t秒后表示的数为(用含t的代数式表示);(2)、动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时与点Q相距4个单位长度?(3)、若M为 的中点,N为 的中点.点P在运动的过程中,线段 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段 的长.