重庆市綦江区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 如果x与2互为相反数,那么|x﹣1|等于( )A、1 B、﹣2 C、3 D、﹣33. 下列各式计算中,正确的是( )A、2a+2=4a B、﹣2x2+4x2=2x2 C、x+x=x2 D、2a+3b=5ab4. 綦江区永辉超市出售的三种品牌大米袋上,分别标有质量为 , , 的字样,从超市中任意拿出两袋大米,它们的质量最多相差( )A、 B、 C、 D、5. 已知方程 ,则移项正确的是( )A、 B、 C、 D、6. 已知: ,则 的值为( )A、-6 B、6 C、9 D、-97. 若方程 的解为 ,则a的值为( )A、-2 B、10 C、22 D、28. 下列图形中,哪一个是正方体的展开图( )A、
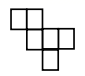 B、
B、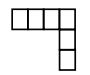 C、
C、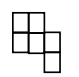 D、
D、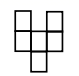 9. 已知如图:数轴上A、B、C、D四点对应的有理数分别是整数a、b、c、d,且 ,则原点应是( )
9. 已知如图:数轴上A、B、C、D四点对应的有理数分别是整数a、b、c、d,且 ,则原点应是( ) A、A点 B、B点 C、C点 D、D点10. 下列图形都是由同样大小的矩形按一定的规律组成,其中,第1个图形中一共有6个矩形,第2个图形中一共有11个矩形,第3个图形中一共有16个矩形,…,按此规律,第7个图形中矩形的个数为( )
A、A点 B、B点 C、C点 D、D点10. 下列图形都是由同样大小的矩形按一定的规律组成,其中,第1个图形中一共有6个矩形,第2个图形中一共有11个矩形,第3个图形中一共有16个矩形,…,按此规律,第7个图形中矩形的个数为( ) A、30 B、36 C、41 D、4511. 新世纪綦江商都一件商品标价为420元,进价为280元,要使利润率为5%,应该打( )折A、9 B、8 C、7 D、612. 已知a,b,c为非零的实数,且不全为正数,则 的所有可能结果的绝对值之和等于( )A、5 B、6 C、7 D、8
A、30 B、36 C、41 D、4511. 新世纪綦江商都一件商品标价为420元,进价为280元,要使利润率为5%,应该打( )折A、9 B、8 C、7 D、612. 已知a,b,c为非零的实数,且不全为正数,则 的所有可能结果的绝对值之和等于( )A、5 B、6 C、7 D、8二、填空题
-
13. 天气预报中,如果零上 3℃记作+3 ℃ ,那么零下 5 ℃记作℃.14. 2020年6且23日,北斗三号最后一颗全球组网卫星从西昌发射中心发射升空,6月30日成功定点于距离地球36000公里的地球同步轨道.将36000用科学记数法表示应为.15. 多项式 是次项式.16. 若 表示最小的正整数, 表示最大的负整数, 表示绝对值最小的有理数,则 .17. 下列说法:①有理数除了正数,就是负数;②相反数大于本身的数是负数;③立方等于本身的数是 ;④若 ,则 其中正确的有:(填序号).18. 某果蔬饮料由果汁、蔬菜汁和纯净水按一定质量比配制而成,纯净水、果汁、蔬菜汁的价格比为 ,因市场原因,果汁、蔬菜汁的价格涨了12.5%,而纯净水的价格降了20%,但并没有影响该饮料的成本(只考虑购买费用),那么该种饮料中果汁与蔬菜汁的质量和与纯净水的质量之比为.
三、解答题
-
19. 计算(1)、 ;(2)、 .20.(1)、解方程: ;(2)、解方程: .21. 先化简,再求值.(1)、 ,其中 , ;(2)、 ,其中 , .22. 如图,点 为线段 上一点,点 为 的中点,且 , .
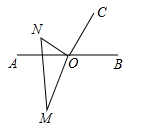
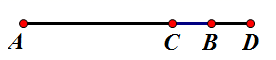 (1)、图中共有条线段,分别是;(2)、求线段 的长;(3)、若点 在直线 上,且 ,求线段 的长.23. 有一个三位数,其百位数字为a,十位数字为b,个位数字为c.若这个三位数百位数字的4倍加上十位数字的2倍,再加上个位数字的和能被8整除,则称这个三位数是“航天数”.如:232, ,故232是“航天数”.(1)、请你写出最小的三位“航天数”;并判断448是否是“航天数”;(2)、请证明任何一个三位“航天数”能被8整除,24. 列方程解应用题,已知A , B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米.甲比乙早出发3小时,乙出发1小时后刚好追上甲.(1)、求甲的速度;(2)、问乙出发之后,到达B地之前,何时甲乙两人相距6千米;(3)、若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地.经过 小时与乙相遇,求此时甲、丙两人之间距离.25. 某文具店今年1月份购进一批笔记本,共2290本.每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.(1)、若该种笔记本在2月份的销售量为2200本,则2月份售价多少元?(2)、由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比2月份在(1)的条件下的售价减少了 ,结果3月份的销量比2月份在(1)的条件下的销售量增加了50%,3月份的销售利润达到6600元,求m的值.26. 如图,点O为直线 上一点,过点O作射线 ,将一直角三角板的直角顶点放在点O处,一边 在射线 上,另一边 在直线 的下方.
(1)、图中共有条线段,分别是;(2)、求线段 的长;(3)、若点 在直线 上,且 ,求线段 的长.23. 有一个三位数,其百位数字为a,十位数字为b,个位数字为c.若这个三位数百位数字的4倍加上十位数字的2倍,再加上个位数字的和能被8整除,则称这个三位数是“航天数”.如:232, ,故232是“航天数”.(1)、请你写出最小的三位“航天数”;并判断448是否是“航天数”;(2)、请证明任何一个三位“航天数”能被8整除,24. 列方程解应用题,已知A , B两地相距60千米,甲骑自行车,乙骑摩托车都沿一条笔直的公路由A地匀速行驶到B地,乙每小时比甲多行30千米.甲比乙早出发3小时,乙出发1小时后刚好追上甲.(1)、求甲的速度;(2)、问乙出发之后,到达B地之前,何时甲乙两人相距6千米;(3)、若丙骑自行车与甲同时出发,沿着这条笔直的公路由B地匀速行驶到A地.经过 小时与乙相遇,求此时甲、丙两人之间距离.25. 某文具店今年1月份购进一批笔记本,共2290本.每本进价为10元,该文具店决定从2月份开始进行销售,若每本售价为11元,则可全部售出;且每本售价每增长0.5元,销量就减少15本.(1)、若该种笔记本在2月份的销售量为2200本,则2月份售价多少元?(2)、由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量,进行了销售调整,售价比2月份在(1)的条件下的售价减少了 ,结果3月份的销量比2月份在(1)的条件下的销售量增加了50%,3月份的销售利润达到6600元,求m的值.26. 如图,点O为直线 上一点,过点O作射线 ,将一直角三角板的直角顶点放在点O处,一边 在射线 上,另一边 在直线 的下方.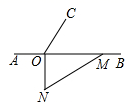 (1)、将上图中的三角板 摆放成如图所示的位置,使一边 在 的内部,当 平分 时, , ;(直接写出结果)
(1)、将上图中的三角板 摆放成如图所示的位置,使一边 在 的内部,当 平分 时, , ;(直接写出结果)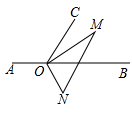 (2)、若 在 的内部,当 平分 ,作线段 的延长线 (如图所示),试说明射线 是 的平分线;
(2)、若 在 的内部,当 平分 ,作线段 的延长线 (如图所示),试说明射线 是 的平分线;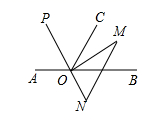 (3)、将(1)问图中的三角板 摆放成如图所示的位置, ,请探究 与 之间的数量关系,并说明理由.
(3)、将(1)问图中的三角板 摆放成如图所示的位置, ,请探究 与 之间的数量关系,并说明理由.