四川省成都市大邑县2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-24 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2021$ 的相反数是（）

A、 $- 2021$ B、 $\frac{1}{2021}$ C、 $- \frac{1}{2021}$ D、 $2021$

查看试题解析
2. 一个正方体的每个面都写有一个汉字.其平面展开图如图所示，那么在该正方体中，和“您”相对的字是（）

A、每 B、天 C、进 D、步

查看试题解析
3. 如图，下列各个图形中，能用∠1，∠AOB，∠O三种方法表示同一角的图形是（）

A、 B、 C、 D、

查看试题解析
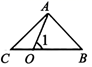4. 2020年12月8日，中国珠峰测量队登顶珠峰半年多时间后，给珠峰测量“身高”的测量结果终于公布，珠穆朗玛峰最新高度为8848.86米.8848.86米用科学记数法表示为（）

A、 88.4886×10² B、8.84886×10³ C、884.886×10¹ D、0.884886×10⁴

查看试题解析
5. 下列调查中，适宜采用全面调查（普查）方式的是（）

A、调查某品牌圆珠笔笔芯的使用寿命 B、调查一批食品的合格情况 C、调查某批次汽车的抗撞击能力 D、调查郫都区复学学生的核酸检测结果

查看试题解析
6. 如果 $2 x^{2} y^{b + 1}$ 与 $- 4 x^{a} y^{3}$ 是同类项，则 $a ， b$ 的值分别是（）

A、 $1 ， 2$ B、 $2 ， 1$ C、 $2 ， 2$ D、 $2 ， 3$

查看试题解析
7. 下列运算正确的是（）

A、 $3 a + 4 a = 7 a^{2}$ B、 $4 a - a = 4$ C、 $a^{3} + 2 a^{2} = 3 a^{5}$ D、 $- \frac{1}{4} a b + 0.25 a b = 0$

查看试题解析
8. 已知 $x = 1$ 是关于x的一元一次方程 $a x + 3 = 2 a - 1$ 的解，则有理数a的值是（）

A、4 B、3 C、2 D、1

查看试题解析
9. 若 $| m | = 5$ ， $| n | = 2$ .且 $m n$ 异号，则 $| m - n |$ 的值为（）

A、 $7$ B、 $3$ 或 $- 3$ C、 $3$ D、 $7$ 或 $3$

查看试题解析
10. 按如图所示的程序计算，若开始输入的数为 $x = 5$ ，则最后输出的结果是（）

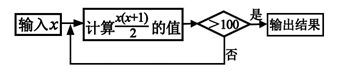A、15 B、30 C、105 D、120

查看试题解析

二、填空题

11. 比较大小： $- \frac{6}{7}$ $- \frac{5}{6}$ .

查看试题解析
12. 如图，A点是数轴上一点，则数轴上距离A点3个单位长度的点表示的数是.

查看试题解析
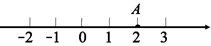13. 已知方程 $2 x^{m - 3} - 5 = 0$ 是关于x的一元一次方程，则常数m的值为.

查看试题解析
14. 从n边形的一个顶点出发，连接其余各顶点，可以将这个n边形分割成17个三角形，则n＝.

查看试题解析
15. 如果 $2 a - 3 b$ 的值为 $- 1$ ，则 $6 b - 4 a + 5$ 的值为.

查看试题解析
16. 点M，N，P在同一直线上，已知 $M N = 7 cm$ ， $N P = 3 cm$ ，则线段 $M P$ 的长是.

查看试题解析
17. 当时刻为下午3:10时，钟表上的时针与分针间的夹角是度.

查看试题解析
18. 我国明代数学读本《算法统宗》一书中有这样一道题：“一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托”.其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺.如果1托为5尺，那么索和竿各为几尺？设竿为x尺，可列方程为.

查看试题解析
19. 如图所示，一系列图案均是长度相同的火柴棒按一定的规律拼搭而成：第1个图案需7根火柴棒，第2个图案需13根火柴棒，……，依此规律，第15个图案需根火柴棒.

查看试题解析

三、解答题

20.

(1)、计算： $- 1^{3} - 7 \times (- \frac{1}{6}) \div (- \frac{1}{6})$

(2)、解方程： $\frac{2 x + 3}{6} - \frac{3 + 2 x}{4} = 5$

查看试题解析
21. 先化简，再求值： $- 5 x^{2} y + 3 (3 y^{2} - x^{3} y) - 2 (- 2 x^{2} y + 3 y^{2} - x^{3} y)$ ，其中 $x = - 1$ ， $y = 2$ .

查看试题解析
22. 由几个相同的边长为1的小立方块搭成的几何体如图所示，排放在桌面上.

(1)、请在下面方格纸中分别画出这个几何体从三个不同的方向（上面、正面和左面）看到的视图；

(2)、根据三个视图，请你求出这个几何体的表面积（不包括底面积）.

查看试题解析
23. 列方程解应用题：2020年4月23日，是第25个世界读书日，我市某书店举办“翰墨书香”图书展.已知《唐诗宋词元曲三百首大全集全6册》和《中华文史大观全8册》两套书的标价总和为1950元，《唐诗宋词元曲三百首大全集全6册》按标价的0.7折出售，《中华文史大观全8册》按标价的3.2折出售，小明花229元买了这两套书，求这两套书的标价各多少元？

查看试题解析
24. 我市教育局发布了“普通中小学校劳动教育状况评价指标”.为了解某校学生一周劳动次数的情况，随机抽取若干学生进行调查，得到如图统计图表：

(1)、这次调查活动共抽取人； $m =$ ； $n =$ ；

(2)、请将条形统计图补充完整；

(3)、若该校学生总人数为2000人，根据调查结果，请你估计该校一周劳动4次及以上的学生人数.

查看试题解析

25. 滴滴快车是一种便捷的出行工具，计费规则如表：

计费项目	里程费	时长费	远途费
单价	1.8元/公里	0.3元/分钟	0.8元/公里
注：车费是里程费、时长费、远途费三部分之和，其中里程费按行车的实际里程计算；时长费按行车的实际时间计算；远途费的收取方式为：行车里程7公里以内（含7公里）不收远途费，超过7公里的，超出部分每公里加收0.8元，不足1公里按1公里计算.

张敏与李良各自乘坐滴滴快车，到同一地点约见，已知到达约见地点时他们的实际行车里程分别为5公里与8公里.设张敏乘车时间为x分钟，李良乘车时间为y分钟.

(1)、则张敏乘车费为元（用含x的代数式表示），李良乘车费为元（用含y的代数式表示）；

(2)、若张敏比李良少支付2元钱，问张敏与李良的乘车时间哪个多？多几分钟？

(3)、在（2）的条件下，已知乘车时间较少的人先到达约见地点等候，等候时间是他自己乘车时间的一半，且比另一人乘车时间的

\frac{1}{3}

少2分钟，问他俩谁先出发？先出发多少分钟？

查看试题解析

26. 如图，A，B两点在数轴上对应的数分别为a，b，且点A在点B的左边， $| a | = 8$ ， $a + b = 12$ ， $a b < 0$ .

(1)、求出a，b的值；

(2)、已知 $A = 2 a^{2} - a b + 2 b^{2}$ ， $B = 3 a^{2} - a b + 3 b^{2}$ ，求 $4 A + [(3 A - B) - 2 (A + B)]$ 的值.

查看试题解析
27. 如图①，已知点 $C 、 D$ 是线段 $A B$ 上两点，D是 $A C$ 的中点，若 $C B = 4 cm$ ， $D B = 7 cm$ .

(1)、求线段 $A B$ 的长；

(2)、如图②，若M，N分别为 $A D$ ， $C B$ 的中点，求线段 $M N$ 的长；

(3)、类比以上探究，如图③，解决以下问题：射线 $O A$ ， $O B$ 分别为 $∠ M O P$ 和 $∠ N O P$ 的平分线， $∠ M O N = α$ ， $∠ N O P = β (β < α)$ .求 $∠ A O B$ 的大小.

查看试题解析
28. 已知：数轴上两点A、B表示的数分别为a，b，点O为原点，且已知a，b满足 $| a + 8 | + {(b - 4)}^{2} = 0$ .

(1)、求 $O A$ ， $O B$ 的长度；

(2)、若点C是线段 $A B$ 上一点（点C不与 $A 、 B$ 两点重合），且满足 $A C = C O + C B$ ，求 $CO$ 的长；

(3)、若动点P，Q分别从A，B两点同时出发，向右运动，点P的速度为2单位长度 $/ s$ ，点Q的速度为1单位长度 $/ s$ .设运动时间为 $t (s)$ ，当点P与点Q重合时，P，Q两点停止运动.求当t为何值时， $2 O P - O Q = 4$ 单位长度.

查看试题解析