四川省成都市成华区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-24 类型:期末考试
一、单选题
-
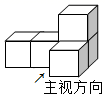
1. 过平面内已知点A作直线,可作直线的条数为( )A、0条 B、1条 C、2条 D、无数条2. 四个有理数:1,﹣2,0,﹣ 中,最大的是( )A、1 B、0 C、﹣ D、﹣23. 如图是由5个相同的正方体组成的几何体,则它的左视图是( )
 A、
A、 B、
B、 C、
C、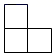 D、
D、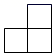 4. 为研究雾霾中各成分的百分比,最适合选用的统计图表是( )A、表格 B、扇形图 C、折线图 D、条形图5. 嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )A、112×103 B、1.12×103 C、1.12×105 D、1.12×1066. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
4. 为研究雾霾中各成分的百分比,最适合选用的统计图表是( )A、表格 B、扇形图 C、折线图 D、条形图5. 嫦娥五号从月球风驰电掣般返回地球的速度接近第二宇宙速度,即112000米/秒,数字112000用科学记数法表示为( )A、112×103 B、1.12×103 C、1.12×105 D、1.12×1066. 把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )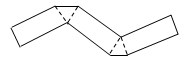 A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥7. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥7. 实数a,b在数轴上的位置如图所示,下列结论中正确的是( )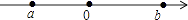 A、a>b B、|a|>|b| C、﹣a<b D、a+b<08. 如图,E是直线 上一点, ,射线 平分 , .则 ( )
A、a>b B、|a|>|b| C、﹣a<b D、a+b<08. 如图,E是直线 上一点, ,射线 平分 , .则 ( ) A、 B、 C、 D、9. 若线段AB=12cm,点C是线段AB的中点,点D是线段AC的三等分点,则线段BD的长为( )A、2cm或4cm B、8cm C、10cm D、8cm或10cm10. 观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是300,则n等于( )A、49 B、50 C、51 D、102
A、 B、 C、 D、9. 若线段AB=12cm,点C是线段AB的中点,点D是线段AC的三等分点,则线段BD的长为( )A、2cm或4cm B、8cm C、10cm D、8cm或10cm10. 观察下列按一定规律排列的n个数:2,4,6,8,10,12,…,若最后三个数之和是300,则n等于( )A、49 B、50 C、51 D、102二、填空题
-
11. 写出一个负数,使这个数的绝对值小于3.12. 要把一根木条在墙上钉牢,至少需要2枚钉子.其中蕴含的数学道理是.13. 某班有52名学生,其中男生人数是女生人数的2倍少17人,则女生有名.14. 如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第 个图案有 个三角形,第 个图案有 个三角形,第 个图案有 个三角形 按此规律摆下去,第 个图案有个三角形(用含 的代数式表示).
 15. 关于x的方程mx|m﹣1|﹣2=0是一元一次方程,则m=.16. 如图,在直角∠AOB的内部作射线OC,若∠AOC=33°24′17″,则∠BOC=.
15. 关于x的方程mx|m﹣1|﹣2=0是一元一次方程,则m=.16. 如图,在直角∠AOB的内部作射线OC,若∠AOC=33°24′17″,则∠BOC=. 17. 把1~9这9个整数填入3×3方格中,使其任意一行,任意一列及两条对角线上的三个数之和都相等,这样便构成了一个“九宫格”.“九宫格”源于我国古代的“洛書”,是世界上最早的“幻方”.在如图的“九宫格”中,x的值为.
17. 把1~9这9个整数填入3×3方格中,使其任意一行,任意一列及两条对角线上的三个数之和都相等,这样便构成了一个“九宫格”.“九宫格”源于我国古代的“洛書”,是世界上最早的“幻方”.在如图的“九宫格”中,x的值为.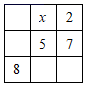 18. 已知整数a1 , a2 , a3 , a4 , 满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,依此类推,则a2021的值为.19. 如图所示,将形状大小完全相同的“▱”按照一定规律摆成下列图形,第1幅图中“▱”的个数为a1 , 第2幅图中“▱”的个数为a2 , 第3幅图中“▱”的个数为a3 , …,以此类推,若 + + +…+ = .(n为正整数),则n的值为 .
18. 已知整数a1 , a2 , a3 , a4 , 满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,依此类推,则a2021的值为.19. 如图所示,将形状大小完全相同的“▱”按照一定规律摆成下列图形,第1幅图中“▱”的个数为a1 , 第2幅图中“▱”的个数为a2 , 第3幅图中“▱”的个数为a3 , …,以此类推,若 + + +…+ = .(n为正整数),则n的值为 .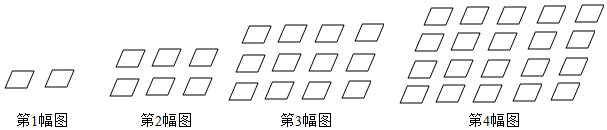
三、解答题
-
20.(1)、计算:100÷22﹣ ×[3﹣(﹣3)2];(2)、计算﹣14﹣( )×12.21.(1)、解方程:3(20+x)+5=2(5x+1);(2)、解方程:x﹣ =1+ .22.(1)、若a=﹣2,b=﹣1,c= ,先化简再求值:3a2b﹣[3a2b﹣(2abc﹣a2c)﹣4a2c]﹣abc.(2)、已知(x﹣3)2+|y+1|=0,先化简再求值:4xy﹣2( x2﹣3xy+2y2)+3(x2﹣2xy).23. 某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数,把乘坐1人、2人、3人、4人、5人的车分别记为A,B,C,D,E五类,由调查所得数据绘制了如图所示的两幅不完整的统计图.
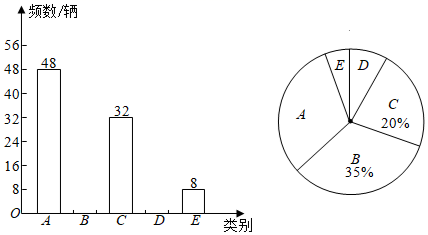 (1)、本次调查的小型汽车共辆,扇形统计图中A类对应的圆心角度数为 , E类对应的圆心角度数为.(2)、补全条形统计图;(3)、若某时段通过该路段的小型汽车数量为5000辆,请你估计其中只乘坐1人的小型汽车数量.24. 某超市采用线上和线下两种方式销售.与2019年相比,该超市2020年销售总额增长了25%,受疫情影响,其中线上销售额增长70%,线下销售额增长10%.已知2019年的销售总额为400万元,线上销售额为x万元.(1)、请用含x的代数式(不用化简)完成下表:
(1)、本次调查的小型汽车共辆,扇形统计图中A类对应的圆心角度数为 , E类对应的圆心角度数为.(2)、补全条形统计图;(3)、若某时段通过该路段的小型汽车数量为5000辆,请你估计其中只乘坐1人的小型汽车数量.24. 某超市采用线上和线下两种方式销售.与2019年相比,该超市2020年销售总额增长了25%,受疫情影响,其中线上销售额增长70%,线下销售额增长10%.已知2019年的销售总额为400万元,线上销售额为x万元.(1)、请用含x的代数式(不用化简)完成下表:2019年
2020年
销售总额(万元)
400
(1+25%)×400
线上销售额(万元)
x
线下销售额(万元)
(2)、求2020年线上销售额与销售总额的百分比.25.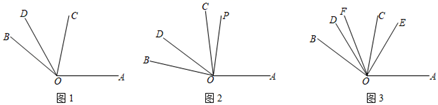 (1)、如图1,∠AOC:∠COD:∠BOD=4:2:1,若∠AOB=140°,求∠BOC的度数;(2)、如图2,∠AOC:∠COD:∠BOD=4:2:1,OP平分∠AOB,若∠AOB=β,求∠COP的度数(用含β的的代数式表示);(3)、如图3,∠AOC=80°,∠BOD=20°,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.26. 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB,延长线段BA到D,使AD:AC=4:3,点M是BD的中点,求线段BD和AM的长度.
(1)、如图1,∠AOC:∠COD:∠BOD=4:2:1,若∠AOB=140°,求∠BOC的度数;(2)、如图2,∠AOC:∠COD:∠BOD=4:2:1,OP平分∠AOB,若∠AOB=β,求∠COP的度数(用含β的的代数式表示);(3)、如图3,∠AOC=80°,∠BOD=20°,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.26. 如图,已知线段AB=3cm,延长线段AB到C,使BC=2AB,延长线段BA到D,使AD:AC=4:3,点M是BD的中点,求线段BD和AM的长度.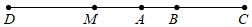 27. 如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题:
27. 如图,以n边形的n个顶点和它内部m个点作为顶点,把原n边形分割成若干个互不重叠的小三角形.观察图形,解答问题: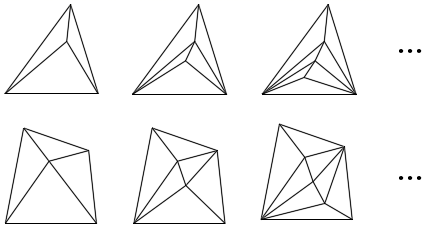 (1)、填表:
(1)、填表:m
n
1
2
3
…
3
3
5
7
…
4
4
…
(2)、填空,三角形内部有m个点,则原三角形被分割成个不重叠的小三角形;四边形内部有m个点,则原四边形被分割成个不重叠的小三角形;n边形内部有m个点,则原n边形被分割成个不重叠的小三角形;(3)、若多边形内部的点的个数为多边形顶点数的五分之一,分割成互不重叠的小三角形共有2021个,求这个多边形的边数.28. 如图,甲、乙两人(看成点)分别在数轴上﹣3和5的位置,沿数轴做移动游戏,规则如下:两人先猜硬币的正反面,依据猜的对错再移动,若都猜对或都猜错,则甲向右移动1个单位,同时乙向左移动1个单位;若甲猜对乙猜错,则甲向右移动4个单位,同时乙向右移动2个单位;若甲猜错乙猜对,则甲向左移动2个单位,同时乙向左移动4个单位. (1)、第一次游戏时,若甲、乙都猜对,则移动后两人相距个单位;若甲猜对乙猜错,则移动后两人相距个单位;若甲猜错乙猜对,则移动后两人相距个单位;(2)、若连续(下次在上次的基础上)完成了10次移动游戏,且每次甲、乙所猜结果均为一对一错.游戏结束后,
(1)、第一次游戏时,若甲、乙都猜对,则移动后两人相距个单位;若甲猜对乙猜错,则移动后两人相距个单位;若甲猜错乙猜对,则移动后两人相距个单位;(2)、若连续(下次在上次的基础上)完成了10次移动游戏,且每次甲、乙所猜结果均为一对一错.游戏结束后,①乙会不会落在原点O处?为什么?
②求甲、乙两人之间的距离.