贵州省遵义市播州区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-24 类型：期末考试

进入出卷网下载

一、单选题

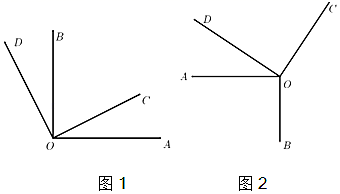
1. 2020的倒数是（）

A、 $- 2020$ B、 $2020$ C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
2. 为满足群众精神文化需要，2016年播州区投入3000万元修建了新图书馆，馆内开设了期刊阅览室、视障读者阅览室、电子阅览室、地方文献室等体验区，其中3000万用科学记数法表示为（）

A、3×10⁸ B、3×10⁷ C、3×10⁶ D、3×10³

查看试题解析
3. 若单项式 $- \frac{1}{3} x y^{3} z^{2}$ 的系数、次数分别是 $a 、 b$ ，则（）

A、 $a = \frac{1}{3}, b = 6$ B、 $a = - \frac{1}{3}, b = 6$ C、 $a = \frac{1}{3}, b = 7$ D、 $a = - \frac{1}{3}, b = 7$

查看试题解析
4. 如图是一个正方体纸盒的展开图，将它折成正方体后与“乡”字相对的面上的字是（）

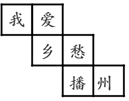A、我 B、爱 C、播 D、州

查看试题解析
5. 下列各组数中，互为相反数的是（）

A、＋3与|﹣3| B、（﹣3）²与﹣3² C、﹣|﹣3|与﹣（＋3） D、＋（﹣3）与﹣|＋3|

查看试题解析
6. 方程 $a - x - (x + 1) = 15$ 的解是 $x = - 2$ ，则a的值是（）

A、 $12$ B、 $- 14$ C、 $18$ D、 $22$

查看试题解析
7. 下列各式运算结果正确的是（）

A、2x＋2y＝4xy B、﹣x＋x＝﹣2x C、7y²﹣4y²＝3 D、8ab²﹣8b²a＝0

查看试题解析
8. 《九章算术》中有一道“盈不足术”的问题：今有人共买物，人出八，盈三；人出七，不足四，问人数几何？译文为：现有一些人共同买一个物品，每人出8元，还盈余3元：每人出7元，还差4元，问共有几人？设共有x人，所列方程正确的是（）

A、8x﹣3＝7x＋4 B、8x＋3＝7x﹣4 C、8x﹣4＝7x＋3 D、3﹣8x＝4＋7x

查看试题解析
9. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数，如图，根据刘徽的这种表示方法，观察图①，可推算图②所得到的数值为（）

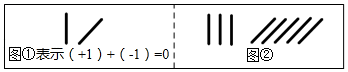A、2 B、﹣2 C、8 D、﹣8

查看试题解析
10. 下列各式进行的变形中，不正确的是（）

A、若 $3 a = 2 b$ ，则 $3 a + 2 = 2 b + 2$ B、若 $3 a = 2 b$ ，则 $3 a - 5 = 2 b - 5$ C、若 $3 a = 2 b$ ，则 $\frac{a}{2} = \frac{b}{3}$ D、若 $3 a = 2 b$ ，则 $9 a = 4 b$

查看试题解析
11. 如果A、B、C三点在同一直线上，且线段AB=6cm，BC=4cm，若M，N分别为AB，BC的中点，那么M，N两点之间的距离为（）

A、5 cm B、1 cm C、5或1 cm D、无法确定

查看试题解析
12. 观察下列式：
$1 - \frac{1}{2} = \frac{1}{2} ， 2 - \frac{2}{5} = \frac{8}{5} ， 3 - \frac{3}{10} = \frac{27}{10} ， 4 - \frac{4}{17} = \frac{64}{17}$ ……

根据你发现的规律，则第10个等式为（）

A、 $9 - \frac{9}{82} = \frac{729}{82}$ B、 $11 - \frac{11}{122} = \frac{1331}{122}$ C、 $10 - \frac{10}{101} = \frac{1000}{101}$ D、 $10 - \frac{10}{99} = \frac{1000}{99}$

查看试题解析

二、填空题

13. 比较大小：﹣0.5 $- \frac{1}{3}$ （填“＞“、“＜“、“＝“）.

查看试题解析
14. 二次三项式﹣3x＋2x²﹣1的一次项系数为.

查看试题解析
15. 已知（x﹣3）²＋|y＋1|＝0，则xy＝.

查看试题解析
16. 已知2a﹣3b＝1，则10﹣2a＋3b的值是.

查看试题解析

三、解答题

17. 计算：

(1)、（ $\frac{1}{3} - \frac{1}{6}$ ）×12＋|﹣2|；

(2)、2 $\frac{2}{3} \times (- \frac{3}{8}) - 5 \div 3 \times \frac{1}{3}$ .

查看试题解析
18. 解方程：

(1)、2（x﹣1）﹣5（2x﹣3）＝0；

(2)、2- $\frac{3 x - 1}{2} = \frac{x + 2}{3}$ .

查看试题解析
19. 先化简，再求值：3a²b﹣[2ab²﹣2（﹣a²b+ab²）]，其中a＝﹣2，b＝ $\frac{1}{2}$ .

查看试题解析
20. 已知x、y互为相反数，a、b互为倒数，m是最大的负整数，求（x＋y）﹣abm的值.

查看试题解析
21. 某农户家准备出售10袋大米，称得质量如下：（单位：千克）
182，180，175，173，182，185，183，181，180，183

(1)、填空：以180千克作为基准数，可用正、负数表示这10袋大米的质量与180的差为；

(2)、试计算这10袋大米的总质量是多少千克？

查看试题解析
22. 在2021年元月份的日历上，用如图的阴影方框任意框出4个数，若设阴影方框右下角的数为a.

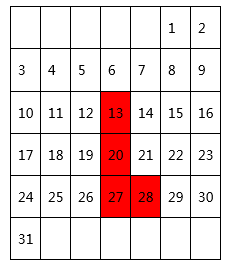(1)、用含a的式子表示框出的4个数的和；

(2)、若框出的4个数之和为68，求a；

(3)、框出的4个数之和可能是39吗？为什么？

查看试题解析
23. 如图1，∠AOB＝∠COD＝90°.

(1)、若∠BOC＝2∠AOC，求∠BOC的大小；

(2)、试探究∠BOC与∠DOA之间的数量关系；

(3)、若把图1中∠AOB绕点O转动到图2的位置，试说明（2）中∠BOC与∠DOA之间的数量关系还成立吗？

查看试题解析
24. 如图，数轴上点A、B分别表示的数是﹣2、6，动点P从A点出发以每秒2个单位长度的速度沿数轴运动，设运动时间为t秒.

(1)、AB长为个单位长度；

(2)、当t＝2时，此时P点表示的数是；

(3)、若另一动点Q从B点处与P点同时出发，以每秒1个单位长度的速度沿数轴运动，经过多少秒后，点P、Q重合.

查看试题解析